具有自适应搜索策略的灰狼优化算法
文章目录
摘要: 灰狼优化算法是一种新型的群智能优化算法。与其他智能优化算法类似,该算法仍存在收敛速度慢、容易陷入局部极小点的点。针对这一问题,提出了具有自适应搜索策略的改进算法。为了提高算法的收敛速度和优化精度,通过适应度值控制智能个体位置,并引入了最优引导搜索方程;另一方面,为提高GWO 的种群多样性,改进算法利用位置矢量差随机跳出局部最优。
1.灰狼优化算法
基础灰狼算法的具体原理参考,我的博客:https://blog.csdn.net/u011835903/article/details/107716390
2. 改进灰狼优化算法
2.1 自适应调整策略
为了进一步提高算法的收敛速度,采用自适应调整策略,将当前个体的适应度值 f i f_i fi与灰狼群的平均适应度值 f a v g f_{avg} favg 进行比较,如果 f i f_i fi 优于 f a v g f_{avg} favg,则继续使用原策略更新灰狼位置;如果 f i f_i fi 次于 f a v g f_{avg} favg,则利用 α , β α ,β α,β 和 δ δ δ 3 个灰狼的适应度值变异灰狼位置。
在变异中,要更新个体的学习较优个体位置信息概率与适应度值成比例,对于原种群里较优个体中适应度值越小的个体,新个体要学习其位置信息的概率会越大。因此,本文对位置更新方程(7)进行改进,创建一个与适应度值成比例的概率分布,并通过该分布求解最优解、优解和次优解。
X ⃗ ( t + 1 ) = { ( 1 f α ) X 1 → + ( 1 f β ) X 2 → + ( 1 f δ ) X 3 → 1 f , f i ⩽ f avg X 1 → + X 2 → + X 3 → 3 , f i > f avg (9) \vec{X}(t+1)=\left\{\begin{array}{ll} \frac{\left(\frac{1}{f_{\alpha}}\right) \overrightarrow{X_{1}}+\left(\frac{1}{f_{\beta}}\right) \overrightarrow{X_{2}}+\left(\frac{1}{f_{\delta}}\right) \overrightarrow{X_{3}}}{\frac{1}{f}}, & f_{i} \leqslant f_{\text {avg }} \\ \frac{\overrightarrow{X_{1}}+\overrightarrow{X_{2}}+\overrightarrow{X_{3}}}{3}, & f_{i}>f_{\text {avg }} \end{array}\right. \tag{9} X(t+1)=⎩⎪⎨⎪⎧f1(fα1)X1+(fβ1)X2+(fδ1)X3,3X1+X2+X3,fi⩽favg fi>favg (9)
1 f = 1 f α + 1 f β + 1 f δ (10) \frac{1}{f}=\frac{1}{f_{\alpha}}+\frac{1}{f_{\beta}}+\frac{1}{f_{\delta}} \tag{10} f1=fα1+fβ1+fδ1(10)
其中, f α , f β f_α , f_β fα,fβ 和 f δ f_δ fδ 分别为 α , β α ,β α,β 和 δ δ δ 的适应度值。
2. 2 跳出局部最优策略
针对种群多样性的变化特征,跳出局部最优策略将智能个体置于不包含当前最优解的区域内,以此来验证算法能够找到不在初始化区域内的最优解 ,增加种群多样性。因此,本文对更新后的位置进行重置,通过最优个体与当前个体之间的位置矢量差随机控制当前个体不在最优解的区域内:
X ⃗ i ′ ( t + 1 ) = X ⃗ α ( t ) + ∣ X ⃗ α ( t ) − X ⃗ i ( t ) ∣ ⋅ r ⃗ (11) \vec{X}_{i}{ }^{\prime}(t+1)=\vec{X}_{\alpha}(t)+\left|\vec{X}_{\alpha}(t)-\vec{X}_{i}(t)\right| \cdot \vec{r}\tag{11} Xi′(t+1)=Xα(t)+∣∣∣Xα(t)−Xi(t)∣∣∣⋅r(11)
其中, 珤 X ⃗ i ′ ( t + 1 ) \vec{X}_{i}{ }^{\prime}(t+1) Xi′(t+1)为跳出局部最优的智能个体位置; X ⃗ i ′ ( t ) \vec{X}_{i}{ }^{\prime}(t) Xi′(t)为位置更新后的智能个体位置; r r r 为[ -2,-1 ]间和[ 1,2 ]间的随机数。
2.3 最优学习搜索方程
虽然标准的 GWO 算法具有初期快速收敛性、良好的全局搜索能力与局部搜索能力之间的平衡性和简单易行等优点,但是随着收敛次数的增加,该算法收敛速度变慢、搜索精度降低而且容易陷入局部最优。受文献[的启发,提出了最优学习搜索方程:
V i , j ( t + 1 ) = w ⋅ V i , j ( t ) + φ i , j ⋅ ( Y i , j ( t ) − X i , j ′ ( t ) ) + μ i , j ⋅ ( X α , j ( t ) − X i , j ′ ( t ) ) (12) \begin{array}{c} V_{i, j}(t+1)=w \cdot V_{i, j}(t)+\varphi_{i, j} \cdot\left(Y_{i, j}(t)-X_{i, j}^{\prime}(t)\right)+ \mu_{i, j} \cdot\left(X_{\alpha, j}(t)-X_{i, j}^{\prime}(t)\right) \end{array} \tag{12} Vi,j(t+1)=w⋅Vi,j(t)+φi,j⋅(Yi,j(t)−Xi,j′(t))+μi,j⋅(Xα,j(t)−Xi,j′(t))(12)
X i , j ′ ′ ( t + 1 ) = X i , j ′ ( t ) + V i , j ( t + 1 ) (13) X_{i, j}^{\prime \prime}(t+1)=X_{i, j}^{\prime}(t)+V_{i, j}(t+1) \tag{13} Xi,j′′(t+1)=Xi,j′(t)+Vi,j(t+1)(13)
其中, V i V_i Vi 为第 i i i 灰狼的当前速度; Y i Y_i Yi为第 i i i灰狼的最优位置; X i ′ X_i^{\prime} Xi′为第 i i i 灰狼的当前位置; X α X_{\alpha} Xα为种群中的最优位置; X i ′ ′ X_i^{\prime\prime} Xi′′ 为学习后的位置; w w w 为惯性权重,一般取 0.8 ; φ i , j \varphi_{i, j} φi,j 和 μ i , j \mu_{i, j} μi,j 分 别 为[-1,1]间和[ 0,1.5]间的随机数。
GWO改进算法的流程:
( 1 )初始化灰狼种群:随机产生 n 个智能个体的位置和速度;初始化 a , A 和 C ;初始化 w ;初始化 X α , Xβ 和 X δ 的值。
( 2 )处理越界智能个体,计算每个智能体的适应度值和灰狼群的平均适应度值 f avg 。
( 3 )比较智能个体的适应度值以及 X α , Xβ和 X δ 的适应度值,确定当前迭代期间的最优解 X α 、优解 Xβ 和次优解 X δ 。
( 4 )根据控制参数 a 随迭代次数增加而线性递减的特性计算各个优解的 A 和 C 。
( 5 )比较当前智能个体的适应度值 fi 与 f avg ,采用式( 9 )
的策略更新当前智能个体的位置。
( 6 )利用式( 11 )使智能个体跳出局部最优解的区域,保留优解 X α , Xβ 和 X δ 。
( 7 )根据式( 12 )和式( 13 ),种群学习最优解搜索方向。
( 8 )输出最优解 X α 和最优值。
( 9 )如果达到结束条件(最大迭代次数或连续 5 次结果相差小于10e-15 ),则结束;否则转到步骤( 2 )。
3.实验结果
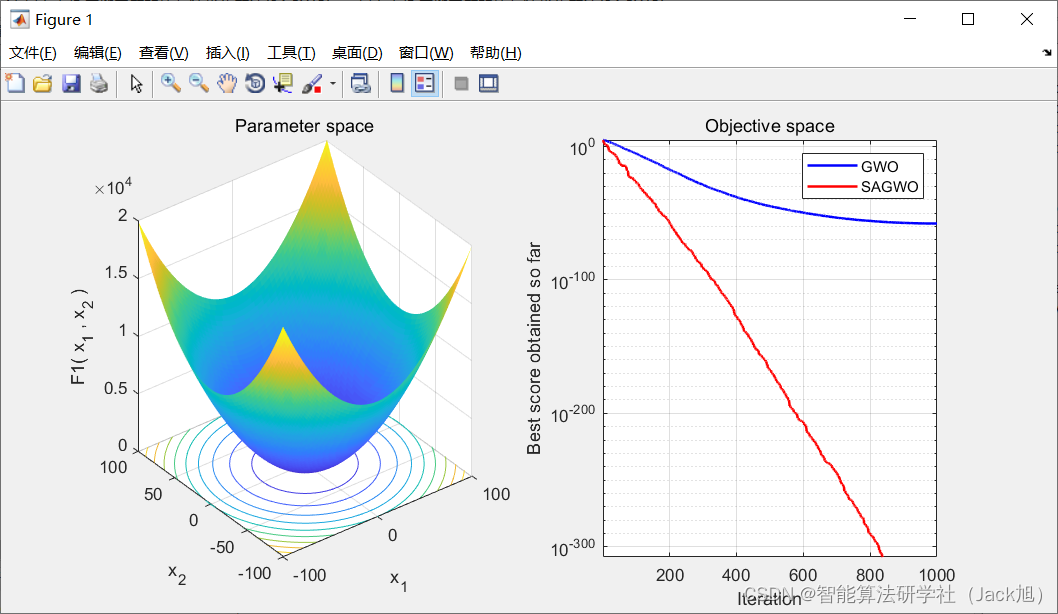
4.参考文献
[1]魏政磊,赵辉,韩邦杰,孙楚,李牧东.具有自适应搜索策略的灰狼优化算法[J].计算机科学,2017,44(03):259-263.