采用动态权重和概率扰动策略改进的灰狼优化算法
文章目录
摘要: 针对基本灰狼优化(GWO)算法存在易陷入局部最优,进而导致搜索精度偏低的问题,提出了一种改进的GWO(IGWO)算法。一方面,通过引入由 GWO 算法系数向量构成的权值因子,动态调整算法的位置向量更新方程;另一方面,通过采用概率扰动策略,增强算法迭代后期的种群多样性,从而提升算法跳出局部最优的能力。
1.灰狼优化算法
基础灰狼算法的具体原理参考,我的博客:https://blog.csdn.net/u011835903/article/details/107716390
2. 改进灰狼优化算法
2.1 引入权值因子
基本 GWO 算法通过计算三个最佳灰狼位置的平均值来更新灰狼位置,这种策略并没有考虑三头狼在群体狩猎活动中的贡献度问题。由于 GWO 算法的 狼 α 并不一定是全局最优解,这时在不断迭代中,随着其余狼 ω 向这三头狼逼近,这就容易陷入局部最优 。本文从最佳灰狼贡献问题角度设计一种权重因子,用来提升GWO算法的寻优能力。由于GWO算法中的系数向量 A 和 C 是动态随机的,而权重因子也应该随着寻优过程非线性调整变化,为此本文设计的权重因子来源于系数向量 A A A 和 C C C 。在基本 G W O \mathrm{GWO} GWO 算法中, A 1 、 A 2 、 A 3 A_{1} 、 A_{2} 、 A_{3} A1、A2、A3 以及 C 1 C_{1} C1 、 C 2 、 C 3 \boldsymbol{C}_{2} 、 \boldsymbol{C}_{3} C2、C3 是不相同的,在这里为了保证权重因子更新的相关联 性, 设计 A 1 、 A 2 \boldsymbol{A}_{1} 、 \boldsymbol{A}_{2} A1、A2 和 A 3 \boldsymbol{A}_{3} A3 相同, C 1 、 C 2 \boldsymbol{C}_{1} 、 \boldsymbol{C}_{2} C1、C2 和 C 3 \boldsymbol{C}_{3} C3 相同, 如下:
A 1 = A 2 = A 3 = 2 a ⋅ r 1 − a C 1 = C 2 = C 3 = 2 r 2 \begin{aligned} &\boldsymbol{A}_{1}=\boldsymbol{A}_{2}=\boldsymbol{A}_{3}=2 a \cdot \boldsymbol{r}_{1}-a \\ &\boldsymbol{C}_{1}=\boldsymbol{C}_{2}=\boldsymbol{C}_{3}=2 \boldsymbol{r}_{2} \end{aligned} A1=A2=A3=2a⋅r1−aC1=C2=C3=2r2
那么, 设计的位置向量权重因子分别为:
w 1 = ∣ A 1 ⋅ C 1 ∣ ∣ A 1 ⋅ C 1 ∣ + ∣ A 2 ⋅ C 2 ∣ + ∣ A 3 ⋅ C 3 ∣ = 1 3 w 2 = ∣ A 2 ⋅ C 2 ∣ w 1 + ∣ A 2 ⋅ C 2 ∣ + ∣ A 3 ⋅ C 3 ∣ = 3 ∣ A 1 ⋅ C 1 ∣ 1 + 6 ∣ A 1 ⋅ C 1 ∣ \begin{aligned} &w_{1}=\frac{\left|\boldsymbol{A}_{1} \cdot \boldsymbol{C}_{1}\right|}{\left|\boldsymbol{A}_{1} \cdot \boldsymbol{C}_{1}\right|+\left|\boldsymbol{A}_{2} \cdot \boldsymbol{C}_{2}\right|+\left|\boldsymbol{A}_{3} \cdot \boldsymbol{C}_{3}\right|}=\frac{1}{3} \\ &w_{2}=\frac{\left|\boldsymbol{A}_{2} \cdot \boldsymbol{C}_{2}\right|}{w_{1}+\left|\boldsymbol{A}_{2} \cdot \boldsymbol{C}_{2}\right|+\left|\boldsymbol{A}_{3} \cdot \boldsymbol{C}_{3}\right|}=\frac{3\left|\boldsymbol{A}_{1} \cdot \boldsymbol{C}_{1}\right|}{1+6\left|\boldsymbol{A}_{1} \cdot \boldsymbol{C}_{1}\right|} \end{aligned} w1=∣A1⋅C1∣+∣A2⋅C2∣+∣A3⋅C3∣∣A1⋅C1∣=31w2=w1+∣A2⋅C2∣+∣A3⋅C3∣∣A2⋅C2∣=1+6∣A1⋅C1∣3∣A1⋅C1∣
w 3 = ∣ A 3 ⋅ C 3 ∣ w 1 + w 2 + ∣ A 3 ⋅ C 3 ∣ = 18 ∣ A 1 ⋅ C 1 ∣ 2 + 3 ∣ A 1 ⋅ C 1 ∣ 18 ∣ A 1 ⋅ C 1 ∣ 2 + 18 ∣ A 1 ⋅ C 1 ∣ + 1 \begin{aligned} w_{3}=& \frac{\left|\boldsymbol{A}_{3} \cdot \boldsymbol{C}_{3}\right|}{w_{1}+w_{2}+\left|\boldsymbol{A}_{3} \cdot \boldsymbol{C}_{3}\right|}=\\ & \frac{18\left|\boldsymbol{A}_{1} \cdot \boldsymbol{C}_{1}\right|^{2}+3\left|\boldsymbol{A}_{1} \cdot \boldsymbol{C}_{1}\right|}{18\left|\boldsymbol{A}_{1} \cdot \boldsymbol{C}_{1}\right|^{2}+18\left|\boldsymbol{A}_{1} \cdot \boldsymbol{C}_{1}\right|+1} \end{aligned} w3=w1+w2+∣A3⋅C3∣∣A3⋅C3∣=18∣A1⋅C1∣2+18∣A1⋅C1∣+118∣A1⋅C1∣2+3∣A1⋅C1∣
因此,得到新的位置更新公式为:
X ( t + 1 ) = w 1 X 1 + w 2 X 2 + w 3 X 3 3 \boldsymbol{X}(t+1)=\frac{w_{1} \boldsymbol{X}_{1}+w_{2} \boldsymbol{X}_{2}+w_{3} \boldsymbol{X}_{3}}{3} X(t+1)=3w1X1+w2X2+w3X3
2. 2 概率扰动策略
随着 GWO 算法迭代次数的不断增加,算法寻优逐渐趋于收敛,一旦收敛于局部最优很难跳出。在算法种群更新中加入扰动机制可以有效提升算法跳出局部最优的能力 。本文设计带有一定概率的扰动来增强算法寻优后期的种群多样性,为摆脱局部收敛创造有利条件。对于概率扰动策略,在以往的一些优化算法中有所研究,如胡宏梅等 提出采用随机概率扰动方式作为基本粒子群算法的全局更新条件,从而增强全局寻优区域的搜索能力,但它采用的是模拟退火算法的退火概率,计算过于复杂;张伟提出在差分进化算法中运用小概率扰动操作来增强种群的多样性,但它采用固定的概率形式,无法在不同迭代过程中充分发挥扰动策略。为此,本文设计一种简便且高效的扰动概率公式为:
P = ( G − 1 ) e ( t − 1 ) / T 4 G P=\frac{(G-1) \mathrm{e}^{(t-1) / T}}{4 G} P=4G(G−1)e(t−1)/T
其中: P P P 为扰动概率; G G G 为优化问题的维度; T T T 为最大迭代次 数。算法迭代初期, 扰动概率较小, 以便算法快速寻找全局最 优解; 算法迭代后期, 扰动概率增加, 增强了种群多样性。一般 来说 T T T 是一个较大的常数, 当算法迭代至后期 t → T t \rightarrow T t→T, 扰动概 率 P = ( 1 − 1 / G ) e ( t / T − 1 / T ) 4 → ( 1 − 1 / G ) e 4 P=\frac{(1-1 / G) \mathrm{e}^{(t / T-1 / T)}}{4} \rightarrow \frac{(1-1 / G) \mathrm{e}}{4} P=4(1−1/G)e(t/T−1/T)→4(1−1/G)e 。灰狼个体进行扰动 的公式为:
M ( t + 1 ) = l b + r 3 ⋅ ( u b − l b ) ; r 3 < P \boldsymbol{M}(t+1)=\boldsymbol{l b}+\boldsymbol{r}_{3} \cdot(\boldsymbol{u} \boldsymbol{b}-\boldsymbol{l b}) ; \quad \boldsymbol{r}_{3}<P M(t+1)=lb+r3⋅(ub−lb);r3<P
其中: M \boldsymbol{M} M 为扰动后的个体; l b \boldsymbol{l b} lb 为灰狼个体位置的下界; u b \boldsymbol{u} \boldsymbol{b} ub 为灰 狼个体位置的上界; ; r 3 ; \boldsymbol{r}_{3} ;r3 为 [ 0 , 1 ] [0,1] [0,1] 之间取值的随机向量。扰动后 的灰狼个体基于贪婪机制进行更新, 更新公式为:
X ( t + 1 ) = { M ( t + 1 ) , f ( M ( t + 1 ) ) < f ( X ( t + 1 ) ) X ( t + 1 ) , 其他 \boldsymbol{X}(t+1)= \begin{cases}\boldsymbol{M}(t+1), & f(\boldsymbol{M}(t+1))<f(\boldsymbol{X}(t+1)) \\ \boldsymbol{X}(t+1), & \text { 其他 }\end{cases} X(t+1)={
M(t+1),X(t+1),f(M(t+1))<f(X(t+1)) 其他
其中: f ( M ( t + 1 ) ) f(\boldsymbol{M}(t+1)) f(M(t+1)) 和 f ( X ( t + 1 ) ) f(\boldsymbol{X}(t+1)) f(X(t+1)) 分别表示第 t + 1 t+1 t+1 代扰动个 体 M \boldsymbol{M} M 和灰狼个体 X \boldsymbol{X} X 的目标函数值。
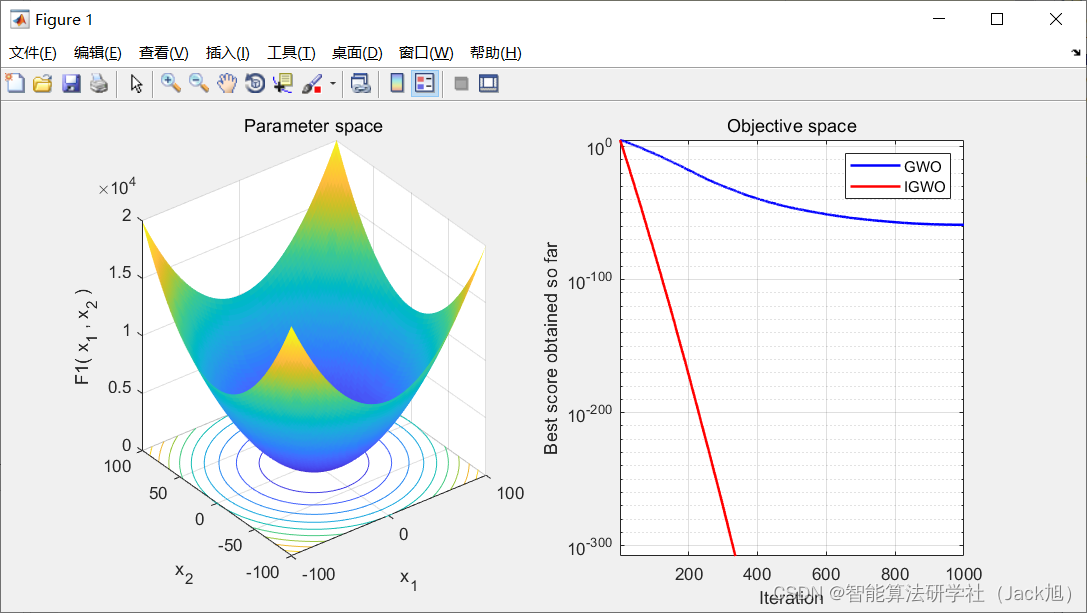
3.实验结果
4.参考文献
[1]陈闯,Ryad Chellali,邢尹.采用动态权重和概率扰动策略改进的灰狼优化算法[J].计算机应用,2017,37(12):3493-3497+3508.