基于自适应调整权重和搜索策略的鲸鱼优化算法
文章目录
摘要:针对鲸鱼优化算法( WOA) 收敛速度慢、收敛精度低、易陷入局部最优的问题,提出一种基于自适应调整权重和搜索策略的鲸鱼优化算法( AWOA) . 设计一种随着鲸鱼种群变化情况而自适应调整权重的方法,提高了算法的收敛速度; 设计一种自适应调整搜索策略,提高了算法跳出局部最优的能力。
1.鲸鱼优化算法
基础鲸鱼算法的具体原理参考,我的博客:https://blog.csdn.net/u011835903/article/details/107559167
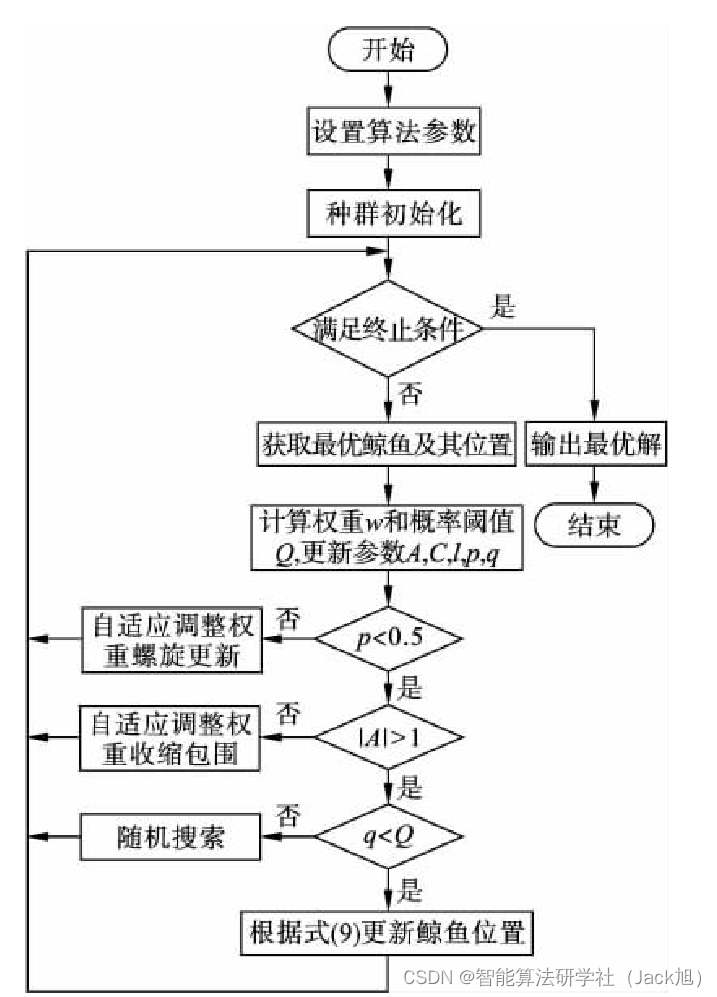
2. 改进鲸鱼优化算法
2.1 自适应调整权重
惯性权重作为鲸鱼优化算法中一个重要的参 数, 对目标函数的优化求解起到了很大的作用. 合 适的权重值对算法寻优能力的提升有很大帮助. 由于 W O A \mathrm{WOA} WOA 在优化求解的过程中, 线性的惯性权 重调整策略若选择不合适, 将影响算法的收敛速 度. 因此, 本文提出了一种根据当前鲸鱼种群分布 情况来自适应改变权值的大小, 公式如下:
w = d 1 ⋅ ( P i worst − P i ibest ) + d 2 ⋅ ( x i upper − x i lower ) / n g ⋅ (5) w=d_{1} \cdot\left(\boldsymbol{P}_{i \text { worst }}-\boldsymbol{P}_{i \text { ibest }}\right)+d_{2} \cdot\left(x_{i}^{\text {upper }}-x_{i}^{\text {lower }}\right) / n_{\mathrm{g}} \cdot \tag{5} w=d1⋅(Pi worst −Pi ibest )+d2⋅(xiupper −xilower )/ng⋅(5)
(5) 式中: n g n_{\mathrm{g}} ng 表示当前种群的迭代次数; x i upper x_{\mathrm{i}}^{\text {upper }} xiupper 和 x i lower x_{\mathrm{i}}^{\text {lower }} xilower 分别为变量 x i x_{i} xi 的上界和下界; P iwort \boldsymbol{P}_{\text {iwort }} Piwort 和 P ibest \boldsymbol{P}_{\text {ibest }} Pibest 分别为 当前鲸鱼种群中最差鲸鱼的位置向量和最优鲸鱼 的位置向量; d 1 d_{1} d1 和 d 2 d_{2} d2 是两个常数. 因此, 当前鲸鱼 个体自适应调整权重收缩包围更新位置和自适应 调整权重螺旋更新位置公式如下:
X ( t + 1 ) = w ⋅ X ∗ ( t ) − A ⋅ D (6) \boldsymbol{X}(t+1)=w \cdot \boldsymbol{X}^{*}(t)-A \cdot \boldsymbol{D} \tag{6} X(t+1)=w⋅X∗(t)−A⋅D(6)
X ( t + 1 ) = w ⋅ X ∗ ( t ) + D p ′ ⋅ e b ⋅ ⋅ cos ( 2 π l ) (7) \boldsymbol{X}(t+1)=w \cdot \boldsymbol{X}^{*}(t)+\boldsymbol{D}_{p}^{\prime} \cdot \mathrm{e}^{b \cdot} \cdot \cos (2 \pi l) \tag{7} X(t+1)=w⋅X∗(t)+Dp′⋅eb⋅⋅cos(2πl)(7)
在引人自适应调整权重搜索策略后, 算法可 以根据当前鲸鱼种群的分布情况自适应地改变权 值的大小. 在算法迭代初期, 若鲸鱼种群陷人局部 最优解, 并且最优解和最差解差别不大时, d 2 ⋅ ( x i upper − x i lower ) / n g d_{2} \cdot\left(x_{i}^{\text {upper }}-x_{i}^{\text {lower }}\right) / n_{\mathrm{g}} d2⋅(xiupper −xilower )/ng 的值并不受种群分布情况的 影响, 这部分的设计依然可以得到较大的权重值 w w w, 避免了算法在迭代初期就陷人小范围搜索的 缺陷; 随着鲸鱼种群迭代次数的增加, d 2 ⋅ ( x i upper − d_{2} \cdot\left(x_{i}^{\text {upper }}-\right. d2⋅(xiupper − x i lower ) / n g \left.x_{i}^{\text {lower }}\right) / n_{\mathrm{g}} xilower )/ng 的值会逐渐变小, 其对权重 w w w 的影响减 小,若此时算法并末得到最优解, d 1 ⋅ ( P iworst − d_{1} \cdot\left(\boldsymbol{P}_{\text {iworst }}-\right. d1⋅(Piworst − P ibest ) \left.\boldsymbol{P}_{\text {ibest }}\right) Pibest ) 的设计就可以对权重值 w w w 起到主导作用, 可以使算法以较大的步长寻优. 这样设计自适应 调整权重 w w w 的好处在于, 其值由两部分决定, 前 半部分对种群迭代次数过大时起主要调节作用, 后半部分对种群陷人局部最优时起主要调节作 用. 权重 w w w 前后两部分会根据当前种群位置的变 化情况而发生变化, 不拘于某种固定的形式, 具 有很强的自适应性.
2.2 自适应调整搜索策略
为防止算法陷入局部最优,随机搜索阶段,个体根据概率阈值 Q 来选取随机搜索的更新方式概率阈值定义为
Q = ∣ f ˉ − f min ∣ ∣ f max − f min ∣ (8) Q=\frac{\left|\bar{f}-f_{\min }\right|}{\left|f_{\max }-f_{\min }\right|} \tag{8} Q=∣fmax−fmin∣∣
∣fˉ−fmin∣
∣(8)
式中: f ˉ \bar{f} fˉ 表示当前鲸鱼种群的平均适应度值; f min f_{\text {min }} fmin 为当前鲸鱼种群中最好的适应度值; f max f_{\max } fmax 为当前鲸 鱼种群中最差的适应度值. 对于每个鲸鱼个体, 以 一个 [ 0 , 1 ] [0,1] [0,1] 之间的随机数 q q q 与计算出的概率阈值 Q Q Q 进行数值比较. 若 q < Q q<Q q<Q, 随机选取的鲸鱼个体 X rand \boldsymbol{X}_{\text {rand }} Xrand 根据式( 9) 更新其位置, 其他鲸鱼个体位置不 变; 否则, 其他鲸鱼个体根据式 (4) 更新其位置. 这样设计使得算法在迭代前期能以较大的概率在 全局范围内随机产生一组解, 避免鲸鱼因聚集在 一起而导致种群多样性的缺失, 增强了算法的全 局搜索能力.
X rand = X j min + r ⋅ ( X j max − X j min ) (9) \boldsymbol{X}_{\text {rand }}=\boldsymbol{X}_{j \text { min }}+r \cdot\left(\boldsymbol{X}_{\boldsymbol{j} \text { max }}-\boldsymbol{X}_{\boldsymbol{j} \text { min }}\right) \tag{9} Xrand =Xj min +r⋅(Xj max −Xj min )(9)
式中: r r r 为 [ 0 , 1 ] [0,1] [0,1] 之间的随机数; X min , X max \boldsymbol{X}_{\text {min }}, \boldsymbol{X}_{\text {max }} Xmin ,Xmax 分别为 变量 X rand \boldsymbol{X}_{\text {rand }} Xrand 取值的最小值和最大值.
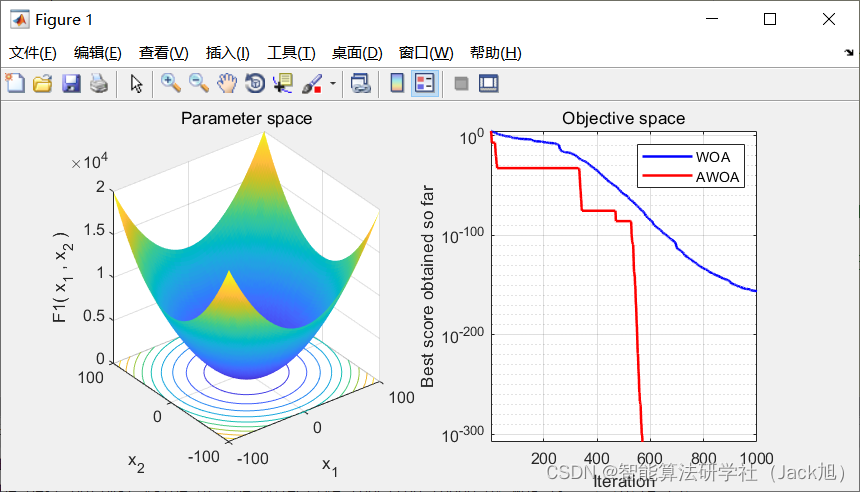
3.实验结果
4.参考文献
[1]孔芝,杨青峰,赵杰,熊浚钧.基于自适应调整权重和搜索策略的鲸鱼优化算法[J].东北大学学报(自然科学版),2020,41(01):35-43.