这个学期一直上网课,全都是看视频,所以没看过书。对于一些知识点只是看PPT理解,所以有很多知识点不知其所以然,最近复习开始看书才发现其中的奥妙,简直是妙不可言。
以下内容来自《计算机组成原理》唐朔飞的教材。
手算乘法对于接受过义务教育的我们应该不是问题,那么我就直接上手算二进制乘法的改进版。
手算二进制的改进
设\(A=0.1101\),\(B=0.1011\),求\(A×B\)。
\[\begin{aligned}A \cdot B &=A \cdot 0.1011 \\&=0.1 A+0.00 A+0.001 A+0.0001 A \\&=0.1 A+0.00 A+0.001(A+0.1 A) \\&=0.1 A+0.01[0 A+0.1(A+0.1 A)] \\&=0.1\{A+0.1[0 A+0.1(A+0.1 A)]\} \\&=2^{-1}\left\{A+2^{-1}\left[0 A+2^{-1}\left(A+2^{-1} A\right)\right]\right\} \\&=2^{-1}\left\{A+2^{-1}\left[0 A+2^{-1}\left(A+2^{-1}(A+0)\right)\right]\right\}\end{aligned} \]
通过上式可见,两数相乘的过程,可以视为加法和位移两种运算,这对计算机来说是非常容易实现的。
下图是具体实现的计算步骤:
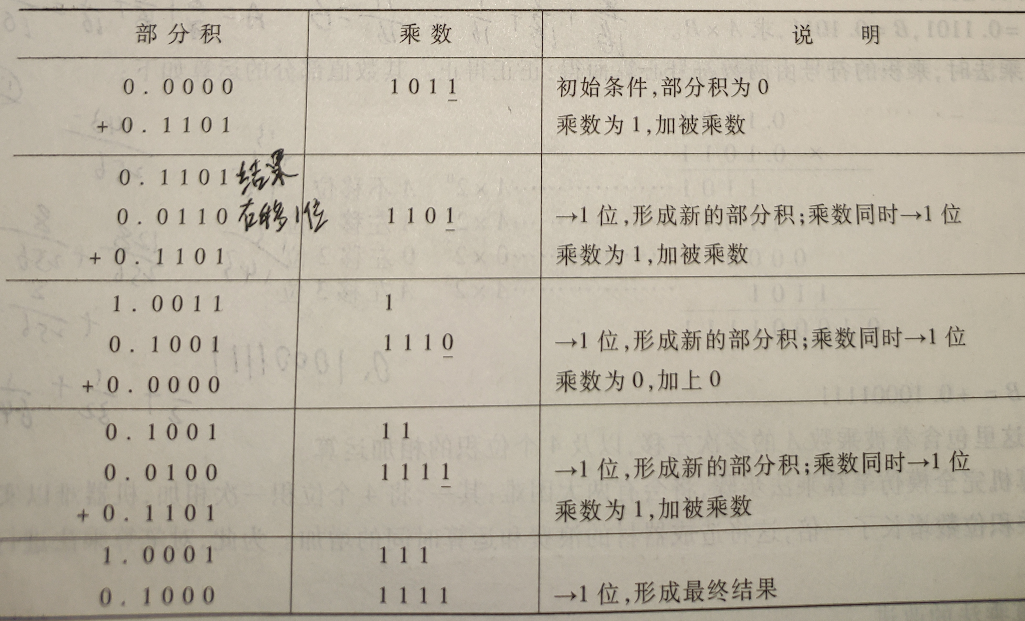
实现上述步骤需要用一个寄存器存放被乘数,一个寄存器存放乘积的高位,另一个寄存器存放乘数和乘积的低位。
原码一位乘法
由于原码与真值之间只相差一个符号,而乘积的符号又可通过两数符号的逻辑异或求得,所以上述运算可直接用于原码一位乘,只需要对符号位进行处理就行了。
原码一位乘运算规则:
\[[x]_原 = x_{0}.x_{1} x_{2} \cdots x_{n} \]
\[[y]_原 = y_{0}.y_{1} y_{2} \cdots y_{n} \]
\[[x]_原·[y]_原=x_0\oplus y_0(0.x_1x_2\cdots x_n)(0.y_{0}.y_{1} y_{2} \cdots y_{n}) \]
式中\(0 . x_{1} x_{2} \cdots x_{n}\)和\(0 . y_{1} y_{2} \cdots y_{n}\)是x和y的绝对值,记作\(x^*\)和\(y^*\)。
补码一位乘法
被乘数$[x]补 = x{0}.x_{1} x_{2} \cdots x_{n} \(,乘数\)[y]补 = y{0}.y_{1} y_{2} \cdots y_{n}$。
- 被乘数x符号任意,乘数y符号为正
\[\begin{equation}\begin{array}{l}{[x]_{\text {补 }}=x_{0} \cdot x_{1} x_{2} \cdots x_{n}=2+x=2^{n+1}+x\ \ (\bmod 2\ )} \\{[y]_{\text {补 }}=0 . y_{1} y_{2} \cdots y_{n}=y} \\{[x]_{\text {补 }} \cdot[y]_{\text {补 }}=[x]_{\text {补 }} \cdot y=\left(2^{n+1}+x\right) \cdot y=2^{n+1} \cdot y+x y}\end{array}\end{equation} \]
下面这一串等式很重要,一定要看懂:
\[\begin{equation}y=0 . y_{1} y_{2} \cdots y_{n}=\sum_{i=1}^{n} y_{i} 2^{-i}, \text { 则 } 2^{n+1} \cdot y=2 \sum_{i=1}^{n} y_{i} 2^{n-i}\end{equation} \]
按照我的理解:\(y_i\)中至少有一个为1,否则\(y=0\),而且\(n≥i\),所以\(2^{n-i}≥1\),可得到\(\sum_{i=1}^{n}y_i2^{n-i}≥1\),进而\(2 \sum_{i=1}^{n} y_{i} 2^{n-i}\)的结果是2的整数倍,所以有 \(2^{n+1}·y=2(\bmod2)\)。
则:
\[[x]_{\text {补 }} \cdot[y]_{\text {补 }}=2^{n+1} \cdot y+x y=2+x y=[x \cdot y]_{\text {补 }} \quad(\bmod 2) \]
即:
\[[x \cdot y]_{\text {补 }}=[x]_{\text {补 }} \cdot[y]_{补}=[x]_{\text {补 }} \cdot y \]
- 被乘数x任意符号,乘数y符号为负
\[\begin{equation}\begin{array}{l}{[x]_{\text {补 }}=x_{0} \cdot x_{1} x_{2} \cdots x_{n}} \\{[y]_{\text {补 }}=1 \cdot y_{1} y_{2} \cdots y_{n}=2+y(\bmod 2)}\end{array}\end{equation} \]
则:
\[\begin{equation}\begin{aligned}y &=[y]_{\text {补 }}-2=1 . y_{1} y_{2} \cdots y_{n}-2=0 . y_{1} y_{2} \cdots y_{n}-1 \\x \cdot y &=x\left(0 . y_{1} y_{2} \cdots y_{n}-1\right) \\&=x\left(0 . y_{1} y_{2} \cdots y_{n}\right)-x\end{aligned}\end{equation} \]
故:
\[\begin{equation}[x \cdot y]_{\text {补 }}=\left[x\left(0 . y_{1} y_{2} \cdots y_{n}\right)\right]_{\text {补 }}+[-x]_{\text {补 }}\end{equation} \]
将\(0 . y_{1} y_{2} \cdots y_{n}\)视为一个正数,正好与上述情况相同。所以:
\[\begin{equation}[x \cdot y]_{\text {补 }}=[x]_{\text {补 }}\left(0 . y_{1} y_{2} \cdots y_{n}\right)+[-x]_{\text {补 }}\end{equation} \]
乘数为负的补码乘法与乘数为正的乘法类似,只需最后加上一项校正项\(-[x]_补\)即可。
需要注意的是:在相加和移位时要按照补码规则进行。
