复球面的一些性质

复球面也叫黎曼球面，它是一种复数表示方法，使球面上的每个点唯一的对应复平面上的一个复数．两者之间构成一一映射，如下图所示，根据初等三角相似的性质，可以推导出复球面上的坐标点和对应复平面上坐标点之间的变换关系，本文试图推到这种关系．

SpRsQ坐标为

    

设其对应的复平面上的点Q坐标为

那么，根据相似三角形比例公式:

另外

所以

所以

所以:

所以：

整理得:

所以:

显然只有满足要求．

所以，复平面上一点对应的复球面坐标为:

关联公式得到了，再看一下有什么规律

换一下形式:

其中

r是复平面上的辐角

所以:

其图形是:

对应的复球面：

---

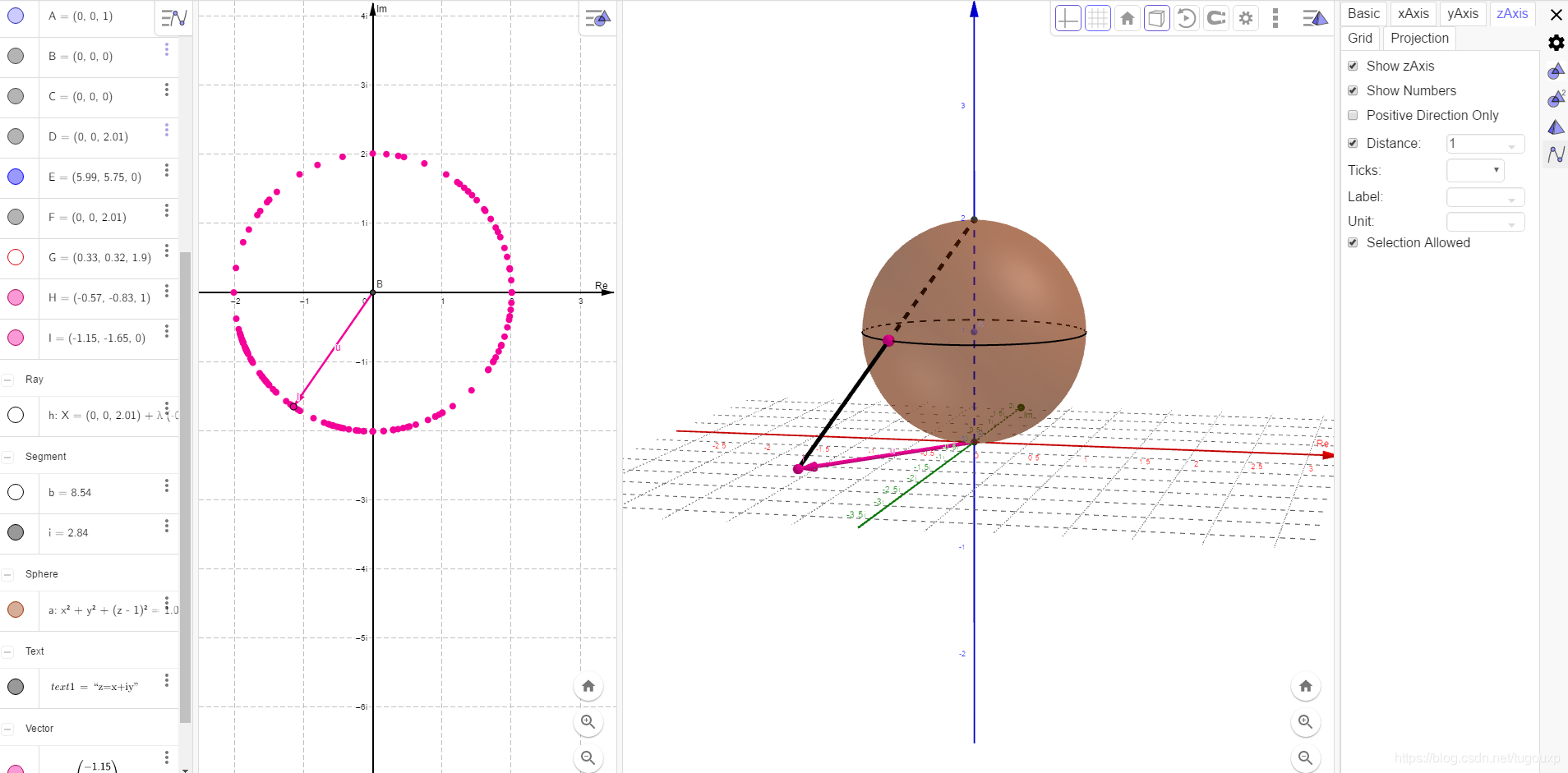
可以看到，以复球面上平行于复平面的大圆对应的复平面大圆半径为界（也就是r=2),z直分别>1和<1

应该有更好的数形结合的求解方法，不过我还没有找到．

结束！