【最优化】二阶收敛算法

二阶收敛算法

不管是前面的最速下降法还是最优梯度法，他们都是线性(一阶)收敛的；而在本章中我们要讨论二阶收敛的优化算法。
该类算法不仅收敛速度加快，并且可以保证在有限步内找到最优解。

从理解的角度，如果一个算法可以在有限步内找到二次函数的最优解的话，我们就说这个算法是二阶收敛的。

---

相关背景概念

最优步长算法性质

在《【最优化】无约束梯度算法》这一篇博文中，我们先是讲述了梯度算法的一般框架，然后确定了最速下降法的迭代形式；接着为了让步长k的选择具有自适应，我们引入了最优步长的思想（每一轮迭代都关于步长k进行一次一维搜索）得到了最优梯度法。

文末，我们给出了结论“最优梯度法相邻两个点的搜索方向一定是正交的”。

该结论在后续的算法中还会用到，且我们需要对其进行推广：

• 使用了【最优步长】思想的算法，其本次迭代点的梯度方向一定与上一次的搜索方向是相互正交的。

【证明】

二次函数及其概念

1. 定义
——常数项、一次项及二次项的组合
（1）标准形式

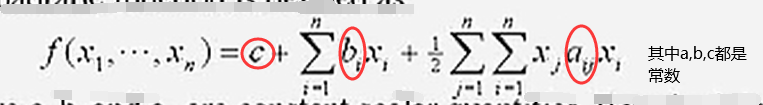
（2）矩阵向量形式

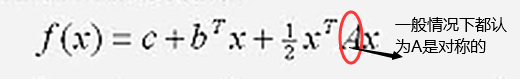
或者说矩阵A总是可以写成对称的形式，因为通过“矩阵向量形式-标准形式”的转换，总能把矩阵A化成对称阵的形式：

2. 性质

（1）如果矩阵A是正定的，那么就称对应的二次函数f(x)是正定二次函数。

p.s. 此处可以类比二次型的定义和分类。

（2）对于二次函数，按照矩阵求导法则，可以得到其梯度向量；如果A是正定矩阵，那么正定二次函数f(x)就有一个唯一的最小值解。

【证明】

共轭方向

1. 共轭的定义
（1）向量的正交
如果两个向量的内积运算结果为0，则说该两个向量是相互正交的。
$$u^{T}v=<u,v>=0$$

（2）相互共轭
定义一个正定阵A，如果两个向量u和v满足u和Av是正交的，则说向量u和v关于矩阵A是共轭的。
$$u^{T}Av=<u,Av>=0$$
特殊地，如果给定一组向量u₁,u₂,…,u_n，且有u_i^TAu_j = 0（i≠j），则成这一组向量u₁,u₂,…,u_n是关于矩阵A相互共轭的；显然，关于同一矩阵共轭的一组向量一定是线性无关的。

正交可以看做是共轭的一种特殊形式，当矩阵A取单位阵I时，u^TAv = u^Tv.

对于任意给定的一个正定阵A，一定可以找到关于其相互共轭的两个向量；在本章二阶收敛算法的讨论下，我们会使用该类特殊向量的方向作为搜索方向，不再使用梯度方向。

2. 算法思想
整体算法的框架与【最优梯度法】保持一致，只不过用共轭搜索方向来替换前者内部的梯度方向。

3. 结论与定理

• 定理：在最优化的每一步采用共轭方向作为搜索方向得到的算法是二阶收敛的。

我们在最开始就说过，讨论【二阶收敛】，只需要验证该算法是否可以在有限步内找到一个正定二次函数的最优解。

• 结论：通过上述的证明，不难发现，【初始点的选择】、【共轭搜索方向的排列顺序】对于算法都没有影响。

4. 示例

本例中共轭的两个向量都是给出的，我们只是通过给出的条件，利用算法进行计算；后续会讲解如何求解出关于某一矩阵共轭的两个向量。

---

共轭方向法

共轭方向法是一类算法的总称，用于描述那些其所有搜索方向都是相互共轭的方法。我们可以通过对前面所讨论的算法诸如【最优梯度法】进行修改得到共轭方向法。
共轭方向法的关键就是找到关于给定矩阵共轭的两个向量。

1. 评价
共轭梯度法介于最速下降法和牛顿法之间，仅需要利用一阶导数信息；客服了最速下降法“收敛速度慢”的缺点，同时也规避了牛顿法“存储和计算二阶导数，开销大”的缺点，是求解大型(非)线性最优化问题的最有效算法之一。

• 无需矩阵存储
• 有较快收敛速度
• 二阶收敛性

2. 一般共轭方向法

共轭梯度法

共轭梯度算法是一个典型的共轭方向算法，它的每一个搜索方向是互相共轭的。而这些搜索方向d_k是负梯度方向-g_k与上一次迭代的搜索方向d_k-1的组合。因此，存储量少，计算方便。
$$d_k=-g_k+{\beta }_{k-1}{d}_{k-1}，其中\beta 为组合系数$$

1. FR共轭梯度算法（Fletcher-Reeves）

p.s. 之前我们讨论了共轭方向法针对正定二次函数是可以在有限步收敛到最优解的，但是上述的算法不仅适用于二次函数；
因此第三步【用当前找到的点xⁿ再替换原先的点x⁰,然后重新开始新的迭代】是必要的。

这些算法在借助计算机实现的时候，会存在计算误差，因此即使求解一个正二次函数的优化问题，也可能存在“无法在有限步收敛”的可能性，因此上述算法的第三步是完全必要的。

2. 简要理解
上述算法对于任意函数都是可行的，我们可以借助正二次函数的特例对其中的共轭方向求解思想进行验证：

在上文的算法中，我们使用FR公式计算得到关于给定矩阵相互共轭的两个向量，也就是FR共轭梯度算法。

3. 示例

4. 评价
在每一轮迭代，虽然只用到了一阶导数的相关信息，但仍然需要对梯度进行计算，计算量依然较为复杂。

---

Powell算法

Powell算法的核心是希望：不求解梯度就能找到相互共轭的两个向量。

它认为：如果两个点x₁和x₂是在不同的初始点沿着相同的搜索方向进行一维搜索找到两个向量，那么在二次函数的优化问题中，向量x₂-x₁就应该和向量v相互正交。

1. 算法思想与框架

综上所述：对于一个n维的无约束优化问题，在给定的循环终止条件未满足的情况下，会持续进行轮次的迭代，每一轮迭代会进行n+1次一维优化搜索，第n+1次搜索会沿着xⁿ-x⁰的方向进行，且用该新的方向【xⁿ-x⁰】替换初始的v⁰搜索方向。

2. 算法过程图解

图源《深度理解Powell优化算法》

上面链接给出的博文对于Powell算法的理论以及优化过程都讨论得很详尽，需要深度理解Powell算法的读者可以戳进原博文中进行了解。

3. 示例

---

拟牛顿法

1. 算法思想概述

牛顿法对于优化问题的成功应用是在于其利用了Hessan矩阵的曲率信息，但是计算Hessan矩阵的工作量很大，且不是所有目标函数都有Hessan矩阵，因此我们联想——
能否仅仅利用目标函数值和一阶导数的信息，构造出目标函数的曲率近似值，从而加快【类牛顿法】的收敛速度。

2. FP拟牛顿法