啊作为一个没学过线代的人……当初写eigenface的时候看PCA看了非常之久……
这里尽量简单的描述这个概念
啊全是随手画的图
基本介绍
需要知道的:
矩阵乘法的本质是坐标变换。
主要通过二维到一维的方式来通俗的描述一下PCA。定义什么可以参考维基之类的。
https://zh.wikipedia.org/wiki/%E4%B8%BB%E6%88%90%E5%88%86%E5%88%86%E6%9E%90
看到下面这幅图上有一堆的二维点。
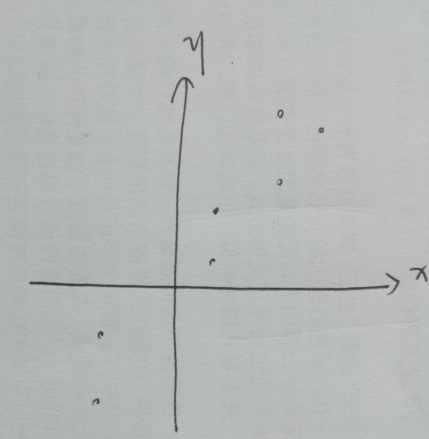
那我们要找一个方式把他转换到一维的。
当然如果考虑非线性就很复杂了……这里就考虑线性的。
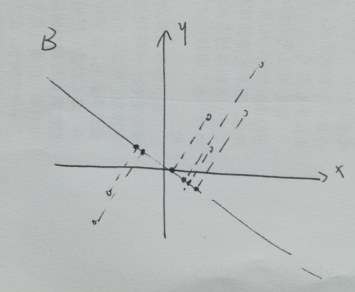
提供AB两种降维方式。实心的点是他们降到一维之后的坐标。
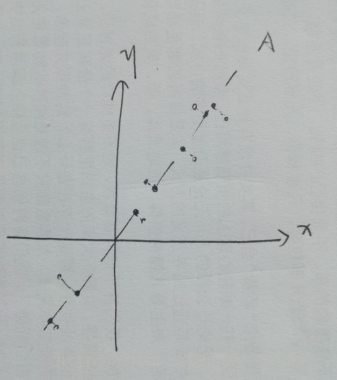
或许这个图看起来可以说是A这种降维【我无数次打出来姜维小哥哥】比较合理,直观上来讲
- 每个点的失真比较小(就空心点到实心点的距离比较小)
- 最后结果比较分散,也就是说在A这条直线上点的差异性得以保留,而在B这条直线上提取出来的更多是它们的共性。
主成分分析中,这种直观的判断方式,被确定为投影之后方差最大
(后来看资料发现两种定义都有)
而经过求解,这个向量正好对应协方差矩阵最大特征值对应的特征向量。(证明放在最后)
那么来一个直观一点的方式……【这里的一些符号定义和下面证明里一样】
如果求出的两个特征向量分别为【markdown公式啥时候那么丑了……预览不是这样的不是!】
那么降到特征空间之后得到的值为
如果不做什么的话是可以正常还原的……
但是需要降维也就是认为
可以省去特征根比较小的点。这些点我们认为体现了更多的“共性”而不是“特性”。
这样还原结果如下【0表示这个维度被省去】
可以看到有一定的失真……但是也可以认为还保留着基本的一些特征【废话】
其他
Q 如果用非人脸图像降维到人脸空间会怎么样?
A 不会怎么样……就,你重构出来可能还是一个脸……失真比较大
就相当于,你提取的特征都是于脸有关的,虽然输入的不是脸但是他依然会提取其中代表人脸的特征……这样
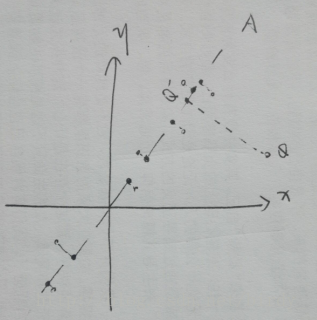
失真差不多和上图那个Q点一样大(比划)因为A不是由他提取出的特征
Q 简化计算
https://zh.wikipedia.org/wiki/%E7%89%B9%E5%BE%81%E8%84%B8
可以参考一下这个……
直观点理解就是,比如在这个二维空间中只有一个点,那么肯定只需要一个特征向量就可以表示它。
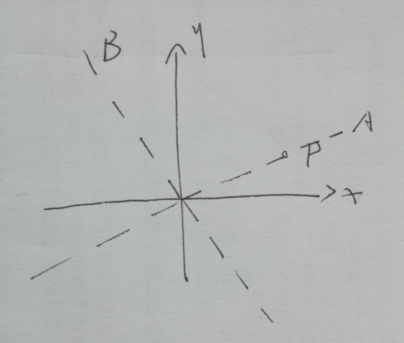
如上图,不管P在什么位置上,肯定可以只用A一个特征向量来表示,它在B上的值肯定是0.因此,我们可以不关心B的这个向量,而只求出A这个向量。
然后这就涉及某些线代的运算了……
Q 其他
我觉得PCA只能保证提取的是一维向量特征的时候,结果是最好的……而不一定能保证提取k维特征的时候最好……主成分分析法的证明过程可以看出,他能保证对于取得的特征根最大的值,一定是方差最大的,而缺少对于提取k维特征是最好的定义。毕竟这样提取的结果也包括方差最小的(特征根最小)。
证明
来自ZJU潘纲老师课件// 后来看到请勿上传外网还是算惹
这个markdown公式长这样毫无重新输一遍的热情……
然后这个链接会全一点 把两种定义都证了
http://www.cnblogs.com/pinard/p/6239403.html