高斯滤波器和LoG(Laplacian of Gaussian)的关系

@[TOC](高斯滤波器和LoG(Laplacian of Gaussian)的关系)

卷积和求导的关系

对于2D函数f(x,y), 其对x的偏导为：
$\frac{\partial f(x,y)}{\partial x}={\lim }_{\epsilon \to 0}\frac{f(x+\epsilon ,y)-f(x,y)}{\epsilon }$
对于离散的数据，我们可以用有限差分去近似其偏导：
$\frac{\partial f(x,y)}{\partial x}\approx \frac{f(x+1,y)-f(x,y)}{1}$
eg:
对下面的老虎图片分别进行x方向和y方向的求导：
x方向求导得到的是竖直方向的边为主
y方向求导得到的是水平方向的边为主

上面的求导就可以用黄色所示的卷积核来近似求导的过程：

• 对于x方向的求导：
  $\frac{\partial f(x,y)}{\partial x}\approx \frac{f(x+1,y)-f(x,y)}{1}$
  这里的x，y表示像素点的位置，（x+1,y）这个点即表示（x,y）的右边的像素点。
• 对于y方向的求导：
  $\frac{\partial f(x,y)}{\partial y}\approx \frac{f(x,y+1)-f(x,y)}{1}$

所以，由上面的例子可知：求导可以用卷积来代替的！

Image gradient

$\frac{\partial f(x,y)}{\partial x}$可以得到竖直方向的边
$\frac{\partial f(x,y)}{\partial y}$可以得到水平方向的边

图像的梯度：

$\nabla f=[\frac{\partial f(x,y)}{\partial x},\frac{\partial f(x,y)}{\partial y}]$

什么是梯度： 梯度的本意是一个向量（矢量），表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着该方向（此梯度的方向）变化最快，变化率最大（为该梯度的模）。

梯度沿着函数值增大的方向！！！

梯度的方向：

$\theta ={\tan }^{-1}(\frac{\partial f(x,y)}{\partial x}/\frac{\partial f(x,y)}{\partial y})$

Effects of noise

找边需要两次卷积操作

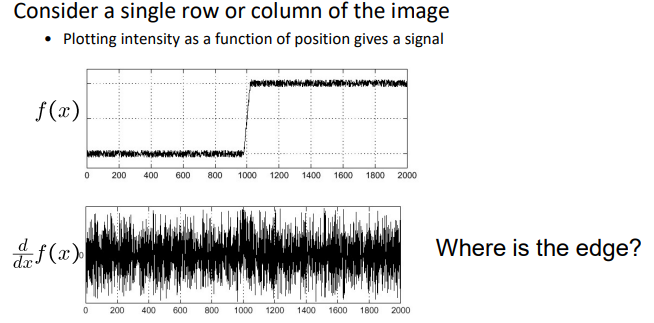
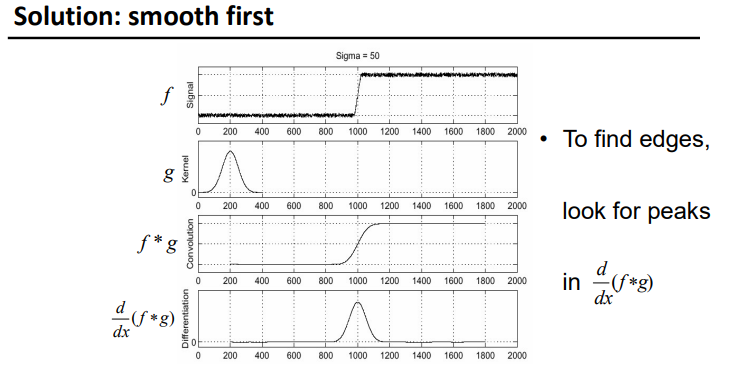
上图中 $g$ 为高斯核，可以平滑噪声，$f\ast g$ 后就没有噪声了，再对 $f\ast g$ 进行求导就可以求出跳跃的位置了。由卷积和求导的关系可知，这里的求导也可以用卷积实现。

所以上图中从f中求出其跳跃的位置需要两次卷积：1. f*g 来去噪 2. 对$f\ast g$进行卷积来求边（即跳跃的位置）

找边只需一次卷积操作

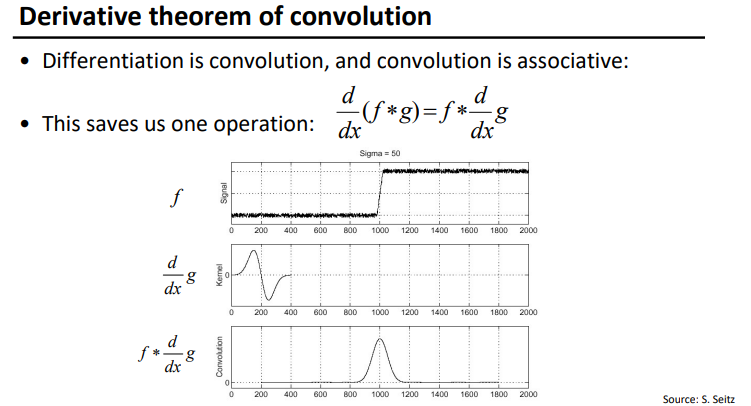
如上图所示，因为$\frac{d}{dx}(f\ast g)=f\ast \frac{d}{dx}g$, 所以我们可以直接先对高斯核进行求导(这个高斯核是我们已知的，所以我们可以提前对高斯核求导)， 再去和 f 卷积。

这样就是把对 f 的处理就变成了 只用 1 次卷积！

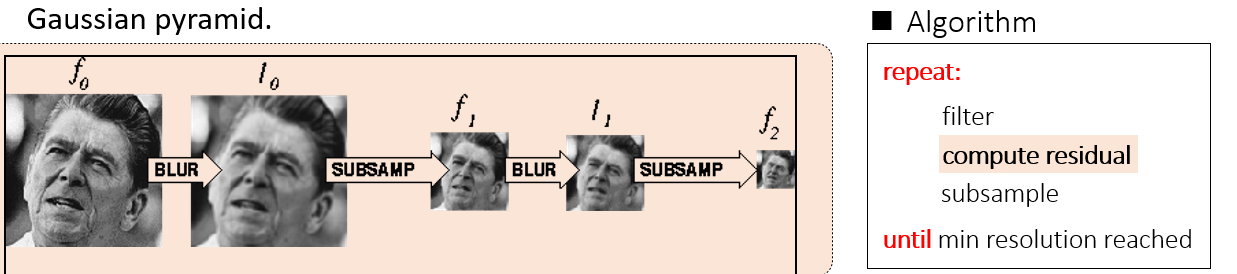
Gaussian pyramid

blur ->subsample ->blur -> subsample

Laplacian of Gaussian(LoG)

Laplacian image pyramid

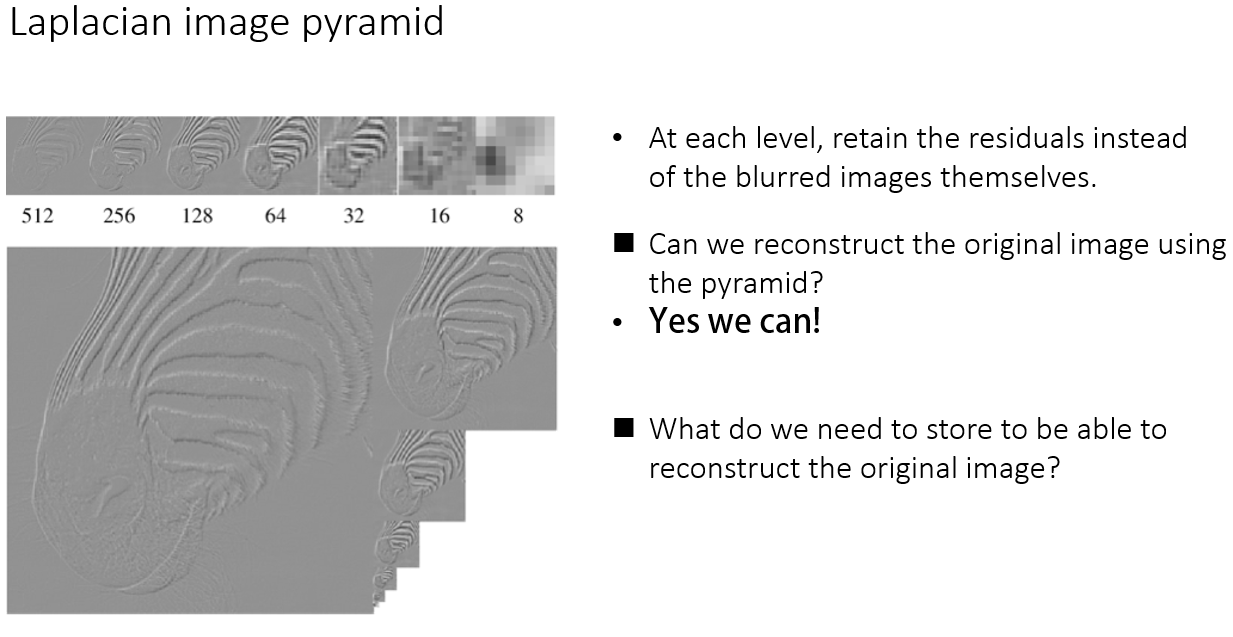
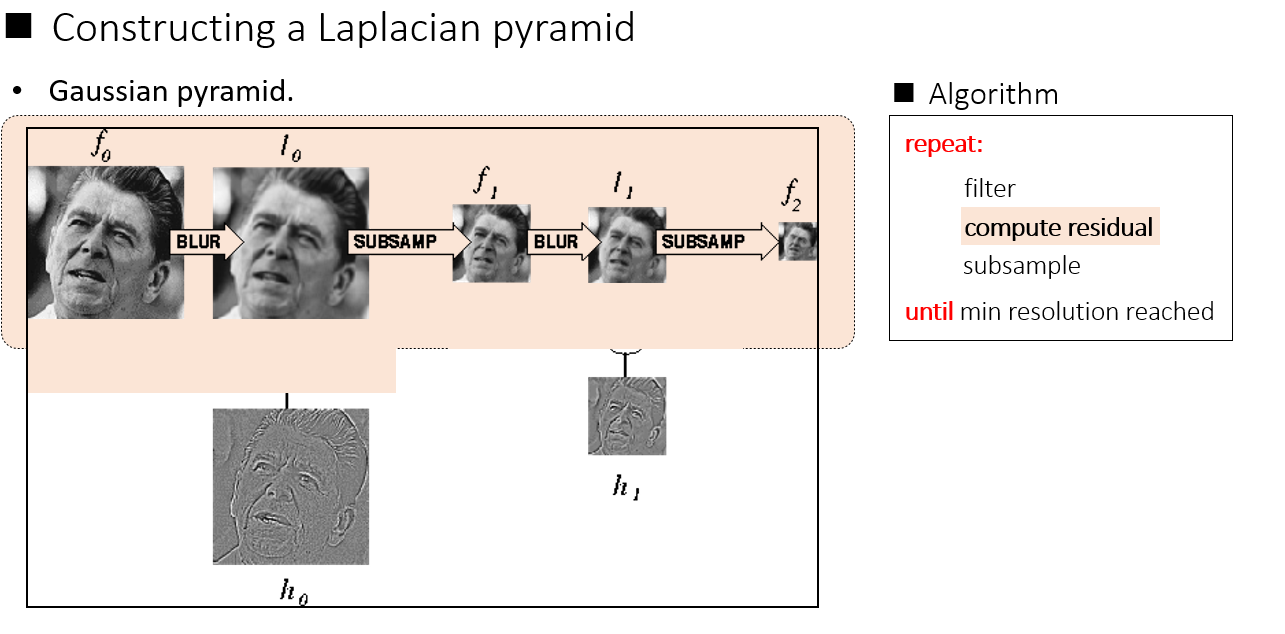
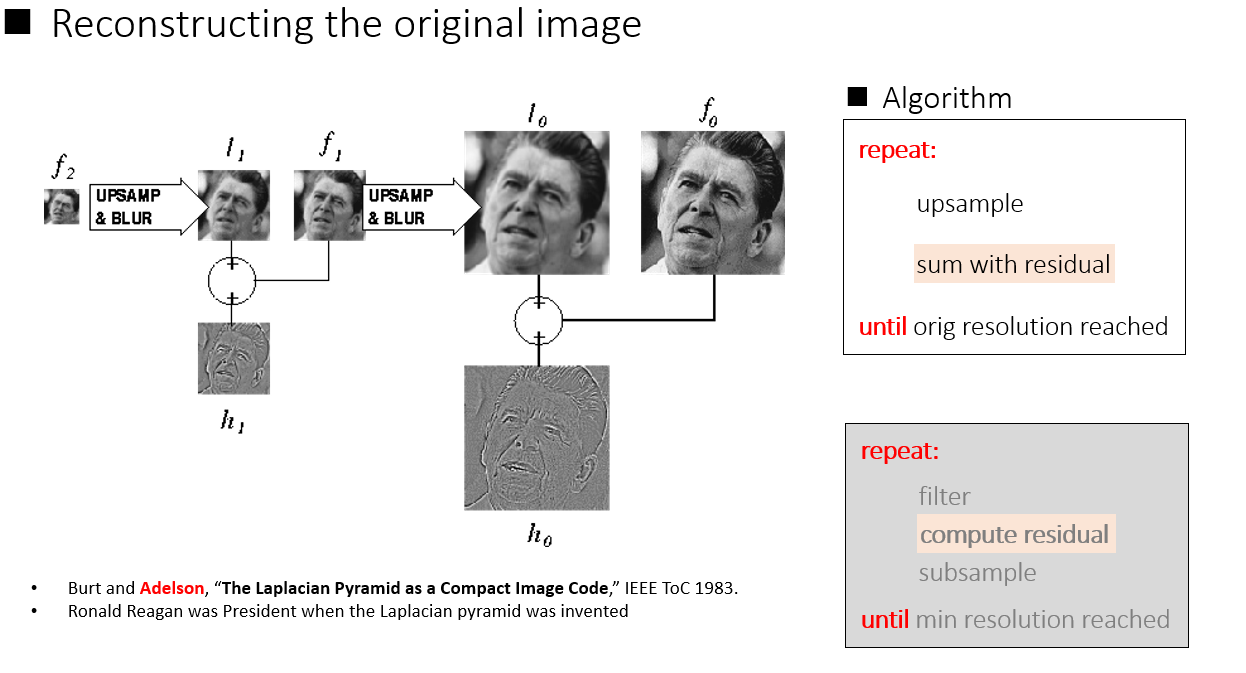
上图的高斯金字塔在存储的时候，需要存储subsample后的原图，而原图的信息量是很大的，所以存储占空间
上图的拉普拉斯金字塔在存储的时候，只需要存储各级残差和最后的一张subsample后的原图即可，对于残差图，很多地方都是0，可以压缩存储，节省存储空间。

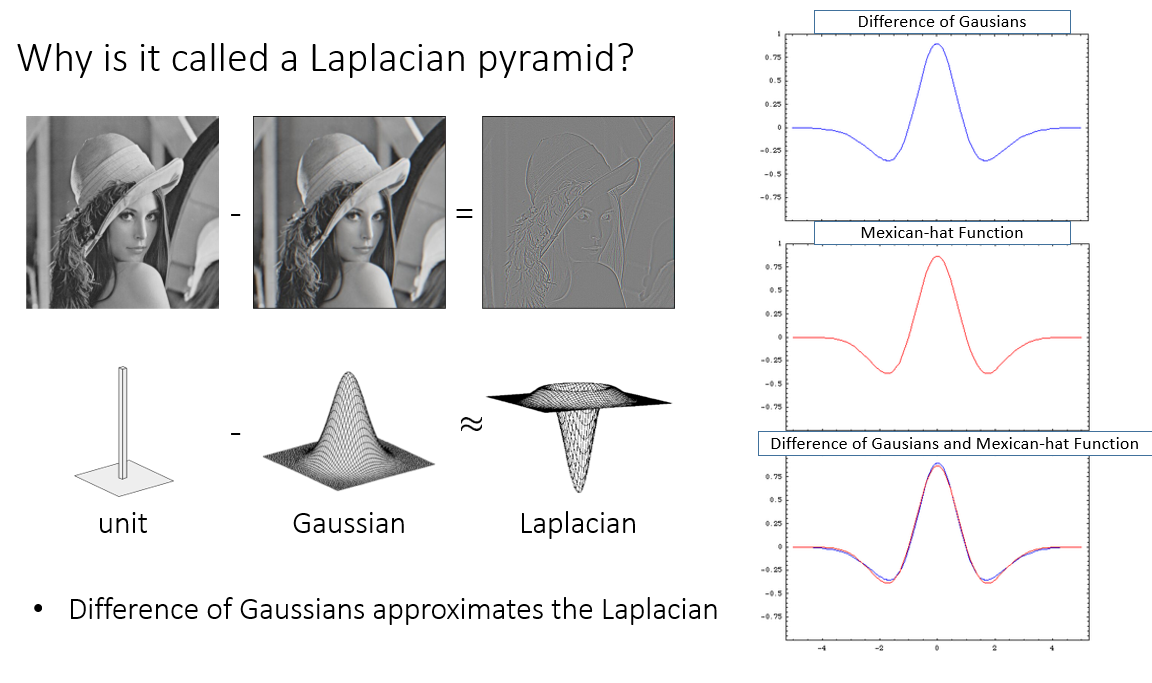
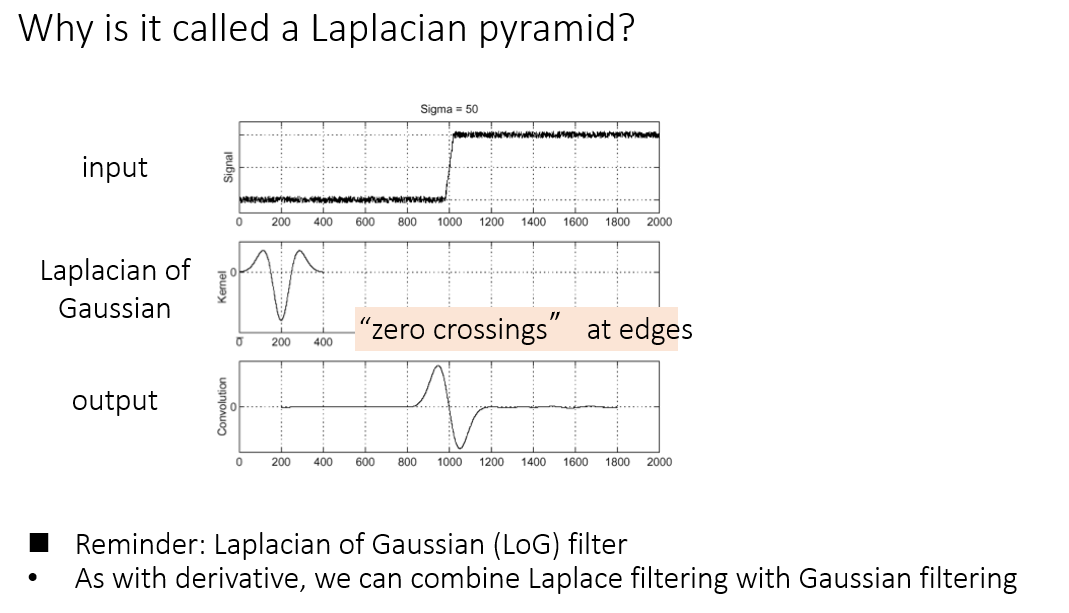
用 Laplacian of Gaussian 也可以去找边的，即卷积后的 zero crossings就是边。

思考：

1. Laplacian of Gaussian是对称的图像？
2. Laplacian of Gaussian 积分为0？
3. Laplacian of Gaussian的$\sigma$越大，“帽子”越矮，“帽子”的范围越大？
   $\sigma =scale=bandwidth$

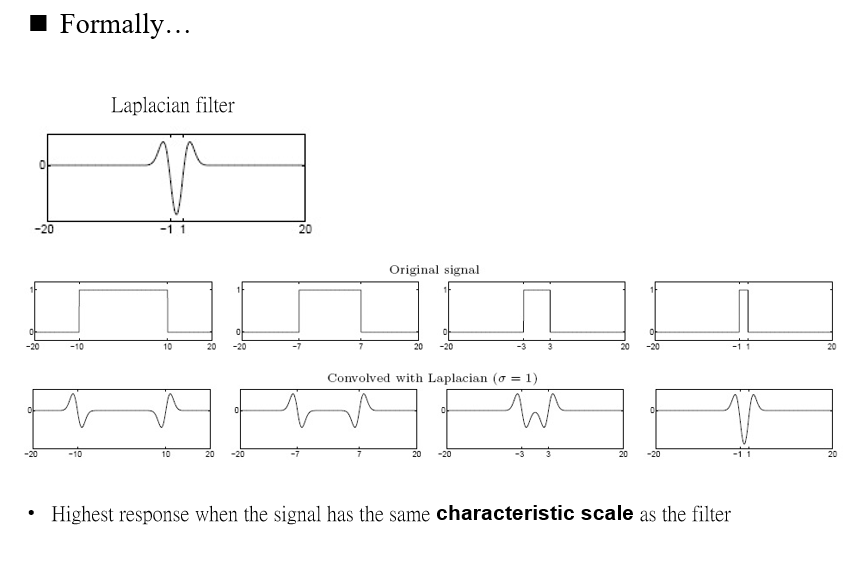
上图中最后一个卷积的结果的峰值最小，说明Laplacian filter和最后一个original signal的 bandwidth 一致（characteristic scale）。受此启发，可以用于多尺度检测

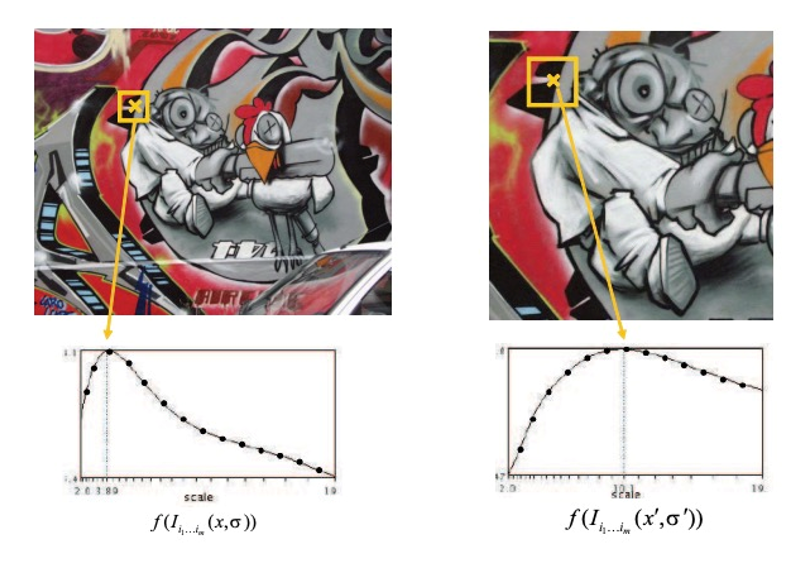
如上图所示，用不同尺度的卷积核去卷积，得到响应值最大的就是尺度相匹配的！

这个知乎讲的怪好！