人工智能：一种现代的方法第三章经典搜索下

文章目录

前言

本部分本书的举例不老套，线索较完整。所以本人便大致依照本书的来讲的，但伪代码还是改为了python代码以便大家理解。

3.5 启发式搜索

3.5.1最佳优先搜索（A搜索）

最佳优先搜索，扩展评估函数f(n)最小的结点
评估函数f(n)=g(n)+h(n)

g(n)是从开始结点到当前结点n的实际路径耗散
h(n)是从当前结点n到目标结点的最小路径耗散的估计值，若n为目标结点，则h(n)=0

3.5.2贪婪最佳搜索

评估函数：g(n)=0，f(n)=h(n)，扩展“离目标最近”的结点“离目标最近”是一个估计值

最优性：非最优
完备性：树搜索，算法不完备，可能陷入死循环

3.5.3 A*搜索

A搜索是A搜索的变体，A算法具有以下性质：假如问题有解，则A*算法一定能找到最优解。

A*搜索如何保证最优性

可采纳性

h(n)是可采纳启发式，不会过高估计到达目标的代价：h(n)<= h*(n)
涵义：f(n)不会超过经过结点n的最优解的实际代价

一致性/单调性

h(n)是一致的，如果对于任意结点n和通过动作a生成的后继结点n’，从n到达目标的估计代价不大于从n到n’的单步代价与从n’到达目标的估计代价之和：h(n)<= c(n,a,n’)+h(n’)
涵义：从n到达目标的估计代价是所有从n到达目标的代价的下界
一致性保证可采纳性

定理1：如果h(n)是可采纳的，那么A*的树搜索版本是最优的

定理2：如果h(n)是一致的，那么A*的图搜索版本是最优的，即一定能找到最优解

import heapq  # 用于实现优先队列

def Astar(graph, start, goal, heuristic):
    queue = []  # 初始化优先队列
    visited = set()  # 初始化已访问节点的集合

    # 将起始节点的路径以及到达该节点的总成本（启发式估计值）加入队列
    # （路径成本+启发式估计值，路径）作为元组存入队列，路径成本+启发式估计值作为优先级
    heapq.heappush(queue, (0 + heuristic[start], [start]))

    while queue:  # 当队列不为空时
        (cost, path) = heapq.heappop(queue)  # 取出当前成本+启发式估计值最小的路径
        node = path[-1]  # 获取路径中的最后一个节点

        if node not in visited:  # 如果该节点没有被访问过
            if node == goal:  # 如果该节点是目标节点
                return path  # 返回该路径

            visited.add(node)  # 将该节点加入已访问节点的集合

            for neighbor in graph[node]:  # 遍历当前节点的所有邻居节点
                new_cost = cost + graph[node][neighbor]  # 计算新路径的总成本
                new_path = list(path)  # 创建一个新路径
                new_path.append(neighbor)  # 将邻居节点加入新路径
                heapq.heappush(queue, (new_cost + heuristic[neighbor], new_path))  # 将新路径加入队列

    return "无解"  # 如果没有从起始节点到目标节点的路径，则返回"无解"

八数码问题
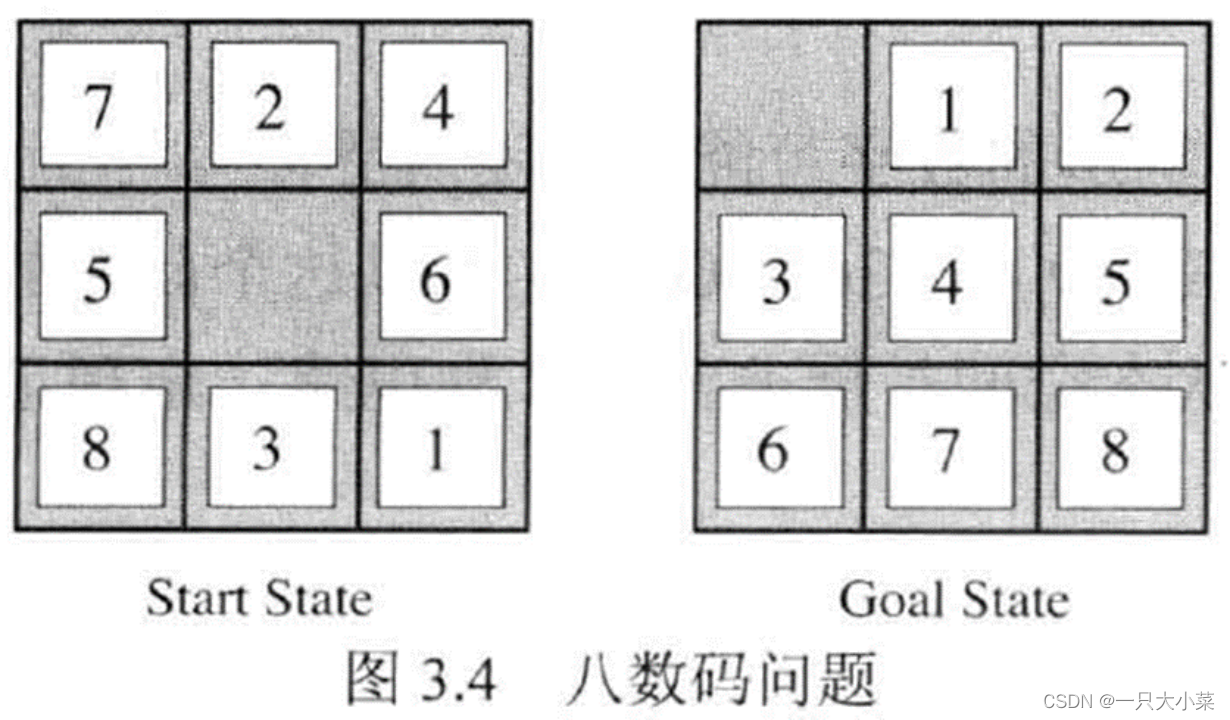
在这里插入图片描述
在一个 3×3的网格中，1∼8这 8个数字和一个 X 恰好不重不漏地分布在这 3×3的网格中。把 X 与上下左右方向数字交换的行动记录为 u、d、l、r。现在，给你一个初始网格，请你通过最少的移动次数，得到正确排列。

string Astar(string start)
{
    
    
    int dx[4] = {
    
    -1, 0, 1, 0}, dy[4] = {
    
    0, 1, 0, -1};
    char op[4] = {
    
    'u', 'r', 'd', 'l'};

    string end = "12345678x";
    unordered_map<string, int> dist;
    unordered_map<string, pair<string, char>> prev;
    priority_queue<pair<int, string>, vector<pair<int, string>>, greater<pair<int, string>>> heap;

    heap.push({
    
    f(start), start});
    dist[start] = 0;

    while (heap.size())
    {
    
    
        auto t = heap.top();
        heap.pop();

        string state = t.second;

        if (state == end) break;

        int step = dist[state];
        int x, y;
        for (int i = 0; i < state.size(); i ++ )
            if (state[i] == 'x')
            {
    
    
                x = i / 3, y = i % 3;
                break;
            }
        string source = state;
        for (int i = 0; i < 4; i ++ )
        {
    
    
            int a = x + dx[i], b = y + dy[i];
            if (a >= 0 && a < 3 && b >= 0 && b < 3)
            {
    
    
                swap(state[x * 3 + y], state[a * 3 + b]);
                if (!dist.count(state) || dist[state] > step + 1)
                {
    
    
                    dist[state] = step + 1;
                    prev[state] = {
    
    source, op[i]};
                    heap.push({
    
    dist[state] + f(state), state});
                }
                swap(state[x * 3 + y], state[a * 3 + b]);
            }
        }
    }

    string res;
    while (end != start)
    {
    
    
        res += prev[end].second;
        end = prev[end].first;
    }
    reverse(res.begin(), res.end());
    return res;
}

3.5.4 存储受限的启发式搜索

迭代加深的A*算法
迭代加深的A算法（IDA）是一种启发式搜索算法，通过逐渐增加搜索深度的方式，在较小的内存消耗下逼近最优解。它结合了深度优先搜索和A*算法的思想，使用启发式函数评估节点代价，并剪枝超过当前最优解代价上界的节点，直到找到最优解或达到搜索限制

def ida_star_search(root, heuristic, cost_limit):
    cost_limit = heuristic(root)  # 初始化代价上界为启发式函数的值
    while True:
        result, cost_limit = depth_limited_search(root, heuristic, cost_limit)
        if result is not None:
            return result

def depth_limited_search(node, heuristic, cost_limit):
    if node is None:
        return None, cost_limit
    if heuristic(node) == 0:
        return node, cost_limit
    if heuristic(node) > cost_limit:
        return None, heuristic(node)  # 返回节点的启发式函数值作为新的代价上界
    min_cost = float('inf')
    for child in expand(node):
        result, new_cost_limit = depth_limited_search(child, heuristic, cost_limit)
        if result is not None:
            return result, cost_limit
        min_cost = min(min_cost, new_cost_limit)
    return None, min_cost

递归最佳优先搜索

模仿只使用线性空间的最佳优先搜索
f_limit：从历史扩展结点得到的最佳候选路径的f值
若当前结点的f值超过了f_limit ，递归调用候选路径
递归回溯时，用当前结点的子结点的最佳f值替换更新当前结点的f值，能记住遗忘的最佳子结点，用于决定以后是否需要重新扩展该子树

def recursive_best_first_search(node, goal, heuristic, f_limit):
    if node == goal:
        return [node], f_limit  # 找到目标节点，返回当前节点作为解决方案和当前节点的f值

    neighbors = get_neighbors(node)  # 获取当前节点的邻居节点

    if not neighbors:
        return None, float('inf')  # 没有邻居节点，无解，返回无穷大的f值

    # 根据启发式评估函数对邻居节点进行排序
    sorted_neighbors = sorted(neighbors, key=lambda n: heuristic(n, goal))

    best_f = float('inf')  # 最佳f值，默认为无穷大
    best_path = None  # 最佳路径，默认为空

    for neighbor in sorted_neighbors:
        f = heuristic(neighbor, goal)
        if f > f_limit:
            return None, f  # 当前节点的f值超过了f_limit，返回无解和当前节点的f值

        result, f = recursive_best_first_search(neighbor, goal, heuristic, f_limit)
        if result is not None and f < best_f:
            best_f = f
            best_path = [node] + result  # 更新最佳f值和路径

    return best_path, best_f  # 返回最佳路径和最佳f值

3.6 启发式函数（以八数码为例）

3.6.1启发式函数的精确度

两个常用的启发式函数

h1 = 不在位的棋子数：h1=8
h2 = 所有棋子到其目标位置的曼哈顿距离和：h2=3+1+2+2+2+3+3+2=18
h1和h2均为可采纳的，但求解性能不同

刻画启发式函数的因素

生成结点数N
有效分支因子b*
若A算法的解路径长度为d，生成结点数为N，则b为深度为d的标准搜索树生成N+1个结点的有效分支因子，满足1+b*+(b*)2+…+(b*)d=N+1
b越小越好（N越小越好），最好情况为1
目标：设计启发式函数，使得b尽可能的小

占优
对于任意结点n， h1(n)<=h2(n)，称h2比h1占优

定理3：若h2比h1占优，采用h2的A算法永远不会比采用h1的A算法扩展更多的结点

每个满足f(n)<C的结点n必将被扩展，且f(n)=g(n)+h(n)，即每个满足h(n)<C-g(n)的结点n必将被扩展采用h2的A搜索扩展的结点必将被采用h1的A搜索扩展

3.6.2 利用松弛问题设计启发式函数

松弛问题：减少动作限制的问题
例. 八数码问题中，若允许每个棋子任意移动位置，则h1是精确步数
例. 八数码问题中，若允许每个棋子可以移动到被其它棋子占据的位置，则h2是精确步数

原问题与松弛问题的关联

减少动作限制导致状态空间图中边可能增加，故减少动作限制的松弛问题的状态空间图是原问题的状态空间图的超图
原问题的最优解是松弛问题的候选解，未必是松弛问题的最优解
松弛问题由于增加的边可能导致捷径，可能存在更好的解

利用松弛问题的最优解代价设计启发式函数

h(n)=hRELAX*(n)<=h*(n)，f(n)<=f*(n)，故该启发式函数是可采纳的
h(n)=hRELAX*(n)，满足三角不等式，故该启发式函数是一致的

例. 八数码问题的松弛问题

原问题的动作描述
棋子可以从方格A移动到方格B，IF A和B水平或竖直相邻，且B是空的
三个松弛问题的动作描述
1. 棋子可以从方格A移动到方格B，IF A和B水平或竖直相邻
1. 棋子可以从方格A移动到方格B，IF B是空的
1. 棋子可以从方格A移动到方格B

新的启发式函数的构造
假定已经设计了无法比较的可采纳的启发式函数h1,h2,…,hm，则可以定义新的启发式函数h(n)=max{h1(n),h2(n),…,hm(n)}

h是可采纳的
h是一致的
h比h1,h2,…,hm均占优

3.6.3利用子问题设计启发式函数

利用子问题的最优解代价设计启发式函数
h(n)=hsub*(n)<=h*(n)，f(n)<=f*(n)，故该启发式函数是可采纳的

3.6.4从经验中学习启发式函数

从经验中学习构造启发式h(n)，即求解大量的八数码问题，每个八数码问题的最优解都成为可供h(n)学习的实例。也就是说，从例子中，学习算法构造h(n)，它能够预测搜索过程中所出现的其他状态的解代价，如n结点的h(n)的表达式。这里的学习算法可以采用包括神经网络、决策树或其他学习技术。

本章总结

本章介绍了在确定性的、可观察的、静态的和完全可知的环境下,Agent 可以用来选择行动的方法。在这种情况下,Agent可以构造行动序列以达到目标;这个过程称为搜索。

在这种环境下，问题由形式化由良定义问题和搜索树抽象为图的问题，再根据问题的规模和要求以及搜索策略的性质选择搜索策略求的解。

搜索策略可分为无信息搜索和有信息搜索，无信息搜索中三个基础的搜索是dfs，bfs，ucs，他们之间差别边缘表的不同，dfs使用栈存储待扩展的节点，bfs使用队列存储待扩展的节点，ucs使用优先队列存储待扩展的节点，深度受限和迭代加深往往再一起使用，它俩是dfs的变体，迭代加深利用深度受限逐渐增加深度来实现Bfs的效果双向搜索可利用dfs或bfs同时搜索减少时间复杂度。

有信息搜索和无信息搜索的区别在于是否有启发函数，而有信息搜索的内部的区别便是评估函数，如果f(x) = 0 ,则是贪婪最佳，如果f(x) != 0,最佳搜索（A搜索），在A搜索的基础上如果h（x）能保证一致性和可采纳性则是A*搜索。

启发函数的设计的好坏往往很能影响搜索的效率，设计启发函数利用松弛问题、子问题、经验中学习等方式。