文章目录
前言
我觉得具体搜索策略的在该书有两点不足,一是伪代码难以理解,二是没有具体例子帮助理解。所以本文用python伪代码代替,以及收集一些例子供大家参考
人工智能:一种现代的方法 第三章 经典搜索 中
3.4 无信息搜索
3.4.1 宽度优先搜索
def BFS(graph, start, goal):
queue = [] # 初始化一个队列
visited = set() # 初始化一个已访问节点的集合
queue.append([start]) # 将起始节点的路径加入队列
while queue: # 当队列不为空时
path = queue.pop(0) # 从队列中取出一个路径
node = path[-1] # 获取路径中的最后一个节点
if node not in visited: # 如果该节点没有被访问过
if node == goal: # 如果该节点是目标节点
return path # 返回该路径
visited.add(node) # 将该节点加入已访问节点的集合
for neighbor in graph[node]: # 遍历当前节点的所有邻居节点
new_path = list(path) # 创建一个新路径
new_path.append(neighbor) # 将邻居节点加入新路径
queue.append(new_path) # 将新路径加入队列
return "无解" # 如果没有从起始节点到目标节点的路径,则返回"无解"
性能分析
- 完备性:若b有限,则算法完备
- 最优性:当动作耗散值相同时,算法最优
- 时间复杂度
在结点被扩展生成时进行目标测试,结点数为b+b2+b3+…+bd=O(b^d)
在结点被选择扩展时进行目标测试,结点数为O(b^(d+1)) - 空间复杂度
探索集O(b^(d-1)) 个结点,边缘集O(b^d)个结点
迷宫问题
一个迷宫,其中的1表示墙壁,0表示可以走的路,只能横着走或竖着走,不能斜着走,要求编程序找出从左上角到右下角的最短路线。
注:利用bfs特殊最优性
void bfs () {
queue <PII> q;
q.push ({
n,n});
memset (pre,-1,sizeof (pre));
pre[n][n] = {
1,1};
while (!q.empty ()) {
PII t = q.front ();
q.pop ();
for (int i = 0;i < 4;i++) {
int a = t.x + dx[i],b = t.y + dy[i];
if (a < 1 || a > n || b < 1 || b > n) continue;
if (g[a][b]) continue;
if (pre[a][b].x != -1) continue;
q.push ({
a,b});
pre[a][b] = t;
}
}
}
3.4.2 一致代价搜索
import heapq # 用于实现优先队列
def UCS(graph, start, goal):
queue = [] # 初始化优先队列
visited = set() # 初始化已访问节点集合
# 将起始节点的路径以及到达该节点的总成本加入队列
# (路径成本,路径)作为元组存入队列,路径成本作为优先级
heapq.heappush(queue, (0, [start]))
while queue: # 当队列不为空时
(cost, path) = heapq.heappop(queue) # 取出当前成本最小的路径
node = path[-1] # 获取路径中的最后一个节点
if node not in visited: # 如果该节点没有被访问过
if node == goal: # 如果该节点是目标节点
return path # 返回该路径
visited.add(node) # 将该节点加入已访问节点的集合
for neighbor in graph[node]: # 遍历当前节点的所有邻居节点
new_cost = cost + graph[node][neighbor] # 计算新路径的总成本
new_path = list(path) # 创建一个新路径
new_path.append(neighbor) # 将邻居节点加入新路径
heapq.heappush(queue, (new_cost, new_path)) # 将新路径加入队列
return "无解" # 如果没有从起始节点到目标节点的路径,则返回"无解"
性能分析
- 若存在耗散值为0的动作NOOP,则可能陷入死循环,算法不完备
若b有限且动作的耗散值均不为0,则算法完备 - 最优性:最优,C*表示最优解路径的耗散值
- 时间复杂度:一致代价搜索>宽度优先搜索
当动作耗散值相同时,除了目标测试的时间点不同之外,一致代价搜索退化为宽度优先搜索

单源最短路问题
有一个 n 个点 m 条边的无向图,请求出从 s 到 t 的最短路长度。
注:利用最优性求解
int dijkstra()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
priority_queue<PII, vector<PII>, greater<PII>> heap;
heap.push({
0, 1});
while (heap.size())
{
auto t = heap.top();
heap.pop();
int ver = t.second, distance = t.first;
if (st[ver]) continue;
st[ver] = true;
for (int i = h[ver]; i != -1; i = ne[i])
{
int j = e[i];
if (dist[j] > dist[ver] + w[i])
{
dist[j] = dist[ver] + w[i];
heap.push({
dist[j], j});
}
}
}
if (dist[n] == 0x3f3f3f3f) return -1;
return dist[n];
}
3.4.3 深度优先搜索
def DFS(graph, start, goal):
stack = [] # 初始化一个栈
visited = set() # 初始化一个已访问节点的集合
stack.append([start]) # 将起始节点的路径加入栈
while stack: # 当栈不为空时
path = stack.pop() # 从栈中取出一个路径
node = path[-1] # 获取路径中的最后一个节点
if node not in visited: # 如果该节点没有被访问过
if node == goal: # 如果该节点是目标节点
return path # 返回该路径
visited.add(node) # 将该节点加入已访问节点的集合
for neighbor in graph[node]: # 遍历当前节点的所有邻居节点
new_path = list(path) # 创建一个新路径
new_path.append(neighbor) # 将邻居节点加入新路径
stack.append(new_path) # 将新路径加入栈
return "无解" # 如果找不到路径,返回“无解”
性能分析
- 时间复杂度最多生成O(b^m)个结点,可能大于状态空间的规模,m可能是无限的
- 空间复杂度(优势)
当一个结点的所有子结点均被探索,则该结点可以删除仅需存储一条从根结点到叶结点的路径,以及该路径上每个结点的所有未被扩展的兄弟结点,O(bm)
深度优先搜索的变体——回溯搜索(一般dfs都由递归实现)
n皇后问题

void dfs(int u)
{
if (u == n)
{
for (int i = 0; i < n; i ++ ) puts(g[i]);
puts("");
return;
}
for (int i = 0; i < n; i ++ )
if (!col[i] && !dg[u + i] && !udg[n - u + i])
{
g[u][i] = 'Q';
col[i] = dg[u + i] = udg[n - u + i] = true;
dfs(u + 1);
col[i] = dg[u + i] = udg[n - u + i] = false;
g[u][i] = '.';
}
}
3.4.4 DFS BFS UCS 之间的对比
| 搜索算法 | 搜索方式 | 最优性 |
|---|---|---|
| 深度优先搜索 (DFS) | 利用栈的后进先出特性,从根节点开始,尽可能深地搜索图的分支,直到当前分支没有更多的节点可以访问,然后回溯到上一个节点,继续搜索下一个分支。 | 不保证找到最短路径。 |
| 广度优先搜索 (BFS) | 利用队列的先进先出特性,从根节点开始,先访问所有的邻居节点,然后再访问邻居的邻居。 | 总是优先搜索离根节点最近的节点,因此它可以找到最短路径(假设所有的边的权重都相同)。 |
| 一致性搜索 (UCS) | 使用优先队列来存储待访问的节点,节点的优先级根据从根节点到该节点的路径的总权重(成本)来确定。 | 总是优先搜索路径成本最小的节点,因此它可以找到最短路径,即使边的权重不相同。 |
3.4.5 深度受限搜索 与迭代加深
迭代加深与深度受限搜索往往结合在一使用,所以本文便放在一起讲解
深度受限搜索
- 添加了深度界限limit(简记为l):深度为l的结点当做叶结点对待
- 完备性:当l<d时,算法不完备
- 最优性:当l>d时,算法非最优
- 时间复杂度:O(b^l)
- 空间复杂度:O(bl)
当l=∞时,深度受限搜索退化为深度优先搜索
迭代加深的深度优先搜索
- 完备性:若b有限,则算法完备
- 最优性:
若路径耗散是结点深度的非递减函数,则算法最优
当动作耗散值相同时,算法最优 - 时间复杂度:db+(d-1)b2+(d-2)b3+…+1bd=O(b^d)
- 空间复杂度:O(b^d)
def IDS(graph, start, goal):
depth = 0 # 初始化深度限制
while True: # 持续搜索,直到找到目标
result = DLS(graph, start, goal, depth) # 进行深度有限搜索
if result != "无解": # 如果找到了解
return result # 返回结果
depth += 1 # 增加深度限制
def DLS(graph, node, goal, depth):
if depth == 0 and node == goal: # 如果达到深度限制且找到目标
return [node] # 返回包含当前节点的路径
elif depth > 0: # 如果还没有达到深度限制
for neighbor in graph[node]: # 遍历当前节点的所有邻居节点
result = DLS(graph, neighbor, goal, depth - 1) # 对邻居节点进行深度有限搜索
if result != "无解": # 如果找到了解
return [node] + result # 返回包含当前节点和找到的路径的路径
return "无解" # 如果没有找到解,返回"无解"
埃及分数问题
把一个分数分为几个不同的分子为 1 的最简分数,要求分成的分数的分母中不能出现
int ok = 0;
for (maxd = 1;; maxd++) {
memset(ans, -1, sizeof(ans));
if (dfs(0, get_first(a, b), a, b)) {
ok = 1;
break;
}
}
// 如果当前解v比目前最优解ans更优,更新ans
bool better(int d) {
for (int i = d; i >= 0; i--) {
if (v[i] != ans[i]) {
return ans[i] == -1 || v[i] < ans[i];
}
}
return false;
}
// 当前深度为d,分母不能小于from,分数之和恰好为aa/bb
bool dfs(int d, int from, LL aa, LL bb) {
if (d == maxd) {
if (bb % aa) return false; // aa/bb必须是埃及分数
v[d] = bb / aa;
if (better(d)) memcpy(ans, v, sizeof(LL) * (d + 1));
return true;
}
bool ok = false;
from = max(from, get_first(aa, bb)); // 枚举的起点
for (int i = from;; i++) {
// 剪枝:如果剩下的maxd+1-d个分数全部都是1/i,加起来仍然不超过aa/bb,则无解
if (bb * (maxd + 1 - d) <= i * aa) break;
v[d] = i;
// 计算aa/bb - 1/i,设结果为a2/b2
LL b2 = bb * i;
LL a2 = aa * i - bb;
LL g = gcd(a2, b2); // 以便约分
if (dfs(d + 1, i + 1, a2 / g, b2 / g)) ok = true;
}
return ok;
}
3.4.6双向搜索
- 两个搜索同时运行:一个从初始状态向前搜索,另一个从目标状态向后搜索,直到状态相遇
- 目标测试:检查两个搜索的边缘集是否相交
性能分析
- 最优性:非最优
- 双向宽度优先搜索的时间复杂度:O(b^(d/2))
- 双向宽度优先搜索的空间复杂度:O(b^(d/2))
- 难点:需要计算父节点的算法和明确的目标状态
3.4.7无信息搜索策略对比
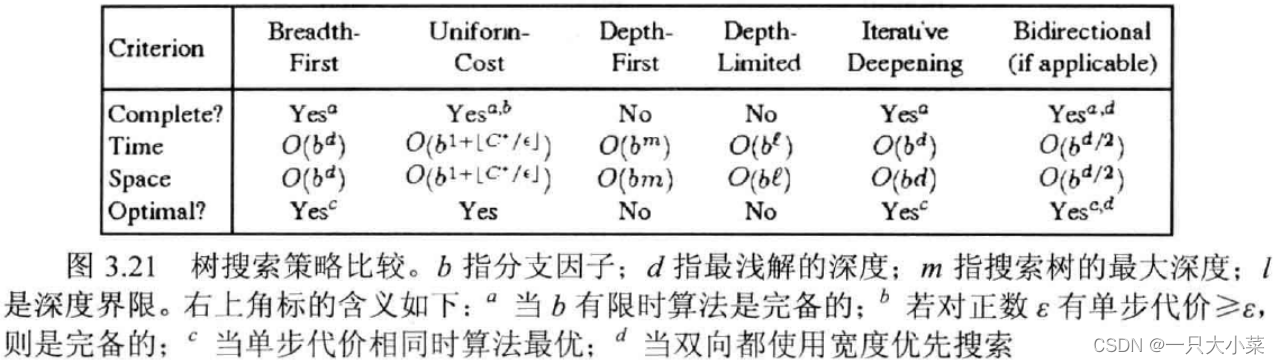
总结
本文讲了具体搜索中无信息算法,并对比了无信息搜索策略性能对比。希望各位能仔细思考之间的关系与差别并深思我收集的例题。
下篇文章将介绍有信息搜索算法,以及启发式函数。不要走开,马上回来,各位敬请期待。