文章目录
前言
人工智能: 一种现代方法 第五章 对抗搜索
5.1 博弈
- 竞争环境:每个Agent的目标之间是冲突的
- 狭义理解,人工智能中的博弈,通常指在完全可观察的环境中,两个Agent
- 轮流执行确定性动作的零和博弈
在博弈搜索中,由于搜索图(树)庞大,A*搜索效率较低。为了提高搜索效率,引入剪枝和启发式评估函数。剪枝允许忽略不影响最终决策的部分,减少搜索空间;启发式评估函数通过估计状态的真实效用值,快速指导搜索方向。综合应用剪枝和启发式评估函数,可以加速博弈搜索,找到较优解决方案

二人博弈
两名玩家:MAX先手,MIN后手
博弈问题的的6个元素:
- s:状态
- Player(s):状态s对应的下棋玩家
- Actions(s):状态s的可选动作集
- Result(s,a):转移模型,下棋动作的结果
- Terminal-Test(s):状态s满足终止测试,游戏结束
- Utility(s,p):玩家p在终止状态s的效用函数值
再次说一句搜索问题两个重要的部分是状态如何定义,以及状态如何转移
井字棋

井字棋游戏的博弈搜索树
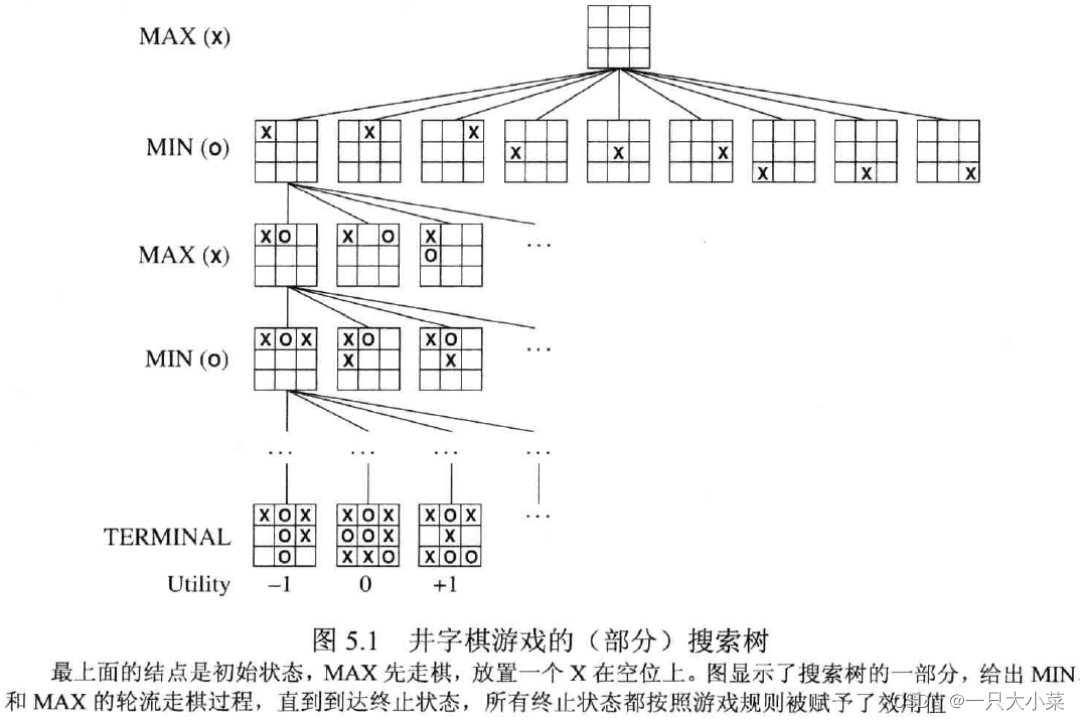
5.2博弈中的决策优化
给定一棵博弈树,最优策略可以通过检查每个结点的极小极大值来决定,记为MINIMAX(n)。假设两个游戏者始终按照最优策略行棋,那么结点的极小极大值就是对应状态的效用值(对于 MAX 而言)。显然地,终止状态的极小极大值就是它的效用值自身。更进一步,对于给定的选择,MAX 喜欢移动到有极大值的状态,而 MIN 喜欢移动到有极小值的状态。所以得到如下公式:
M i n M a x ( s ) : MinMax(s): MinMax(s):
- U t i l i t y ( s ) , s 为终止状态 Utility(s),s为终止状态 Utility(s),s为终止状态
- M a x a i n A c t i o n s ( s ) M i n M a x ( R e s u l t ( s , a ) ) , s 为 M A X 结点 Max_{a in Actions(s)}MinMax(Result(s,a)),s为MAX结点 MaxainActions(s)MinMax(Result(s,a)),s为MAX结点
- M i n a i n A c t i o n s ( s ) M i n M a x ( R e s u l t ( s , a ) ) , s 为 M I N 结点 Min_{a in Actions(s)}MinMax(Result(s,a)),s为MIN结点 MinainActions(s)MinMax(Result(s,a)),s为MIN结点
5.2.1 极大极小值搜索
def minimax(node, maximizing_player):
if node.is_terminal_node():
return node.evaluate() # 评估当前节点的得分
if maximizing_player:
best_value = float('-inf')
for child_node in node.get_children():
value = minimax(child_node, False)
best_value = max(best_value, value)
return best_value
else:
best_value = float('inf')
for child_node in node.get_children():
value = minimax(child_node, True)
best_value = min(best_value, value)
return best_value
性能分析
m为搜索树的最大深度,b为平均分支因子
- 时间复杂度:O(b^m)
- 空间复杂度 :
一次性生成所有后继结点:O(bm)
每次生成一个后继结点:O(m)
5.2.2多人博弈
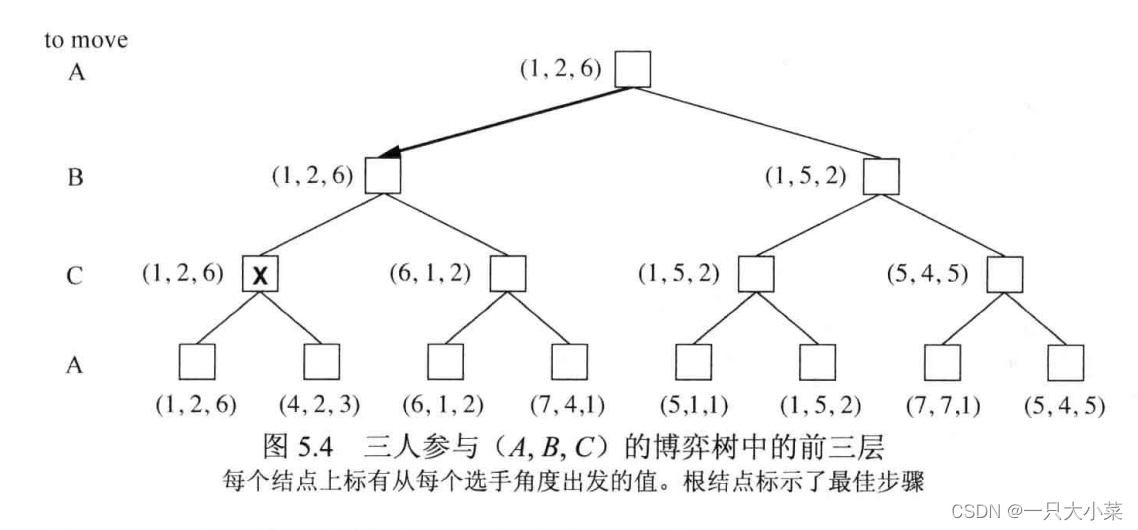
最简单实现方式:让函数UTILITY返回一个向量
5.3 alpha- beta剪枝
alpha= 到目前为止路径上发现的MAX的最佳(即极大值)选择
beta = 到目前为止路径上发现的 MIN 的最佳即极小值)选择
alpga-beta搜索中不断更新alpha 和beta 的值,并且当某个结点的值分别比目前的 MAX 的alpha 或者 MIN的beta 值更差的时候剪裁此结点剩下的分支(即终止递归调用)将这一点应用到极大极小值搜索
def alpha_beta(node, alpha, beta, maximizing_player):
if node.is_terminal_node():
return node.evaluate() # 评估当前节点的得分
if maximizing_player:
value = float('-inf')
for child_node in node.get_children():
value = max(value, alpha_beta(child_node, alpha, beta, False))
alpha = max(alpha, value) # 更新alpha值,记录最佳极大值选择
if alpha >= beta:
break # 执行剪枝,停止继续搜索该节点的兄弟节点
return value
else:
value = float('inf')
for child_node in node.get_children():
value = min(value, alpha_beta(child_node, alpha, beta, True))
beta = min(beta, value) # 更新beta值,记录最佳极小值选择
if alpha >= beta:
break # 执行剪枝,停止继续搜索该节点的兄弟节点
return value
普通MaxMin算法:O(b^m)
alpha-beta剪枝最佳情况:O(b^(m/2))
5.4 实时决策
博弈搜索通常要求在合理的时间范围内行棋,需要增加博弈搜索树的深度限制
以alpha_beta为例
def alpha_beta(node, depth, alpha, beta, maximizing_player):
if depth == 0 or node.is_terminal_node():
return node.evaluate() # 评估当前节点的得分
if maximizing_player:
value = float('-inf')
for child_node in node.get_children():
value = max(value, alpha_beta(child_node, depth - 1, alpha, beta, False))
alpha = max(alpha, value) # 更新alpha值,记录最佳极大值选择
if alpha >= beta:
break # 执行剪枝,停止继续搜索该节点的兄弟节点
return value
else:
value = float('inf')
for child_node in node.get_children():
value = min(value, alpha_beta(child_node, depth - 1, alpha, beta, True))
beta = min(beta, value) # 更新beta值,记录最佳极小值选择
if alpha >= beta:
break # 执行剪枝,停止继续搜索该节点的兄弟节点
return value
好的评估函数
- 评估函数对终止状态的排序:获胜的评估值好于平局,平局的评估值好于落败
- 评估函数的计算本身的时间开销不能太大
- 对于非终止状态,评估函数值应与获胜几率密切相关
- 实际应用中,通常采用特征的线性加权函数 :Eval(s)=w1f1(s)+w2f2(s)+…+wnfn(s)
5.5 随机博弈
西洋双陆棋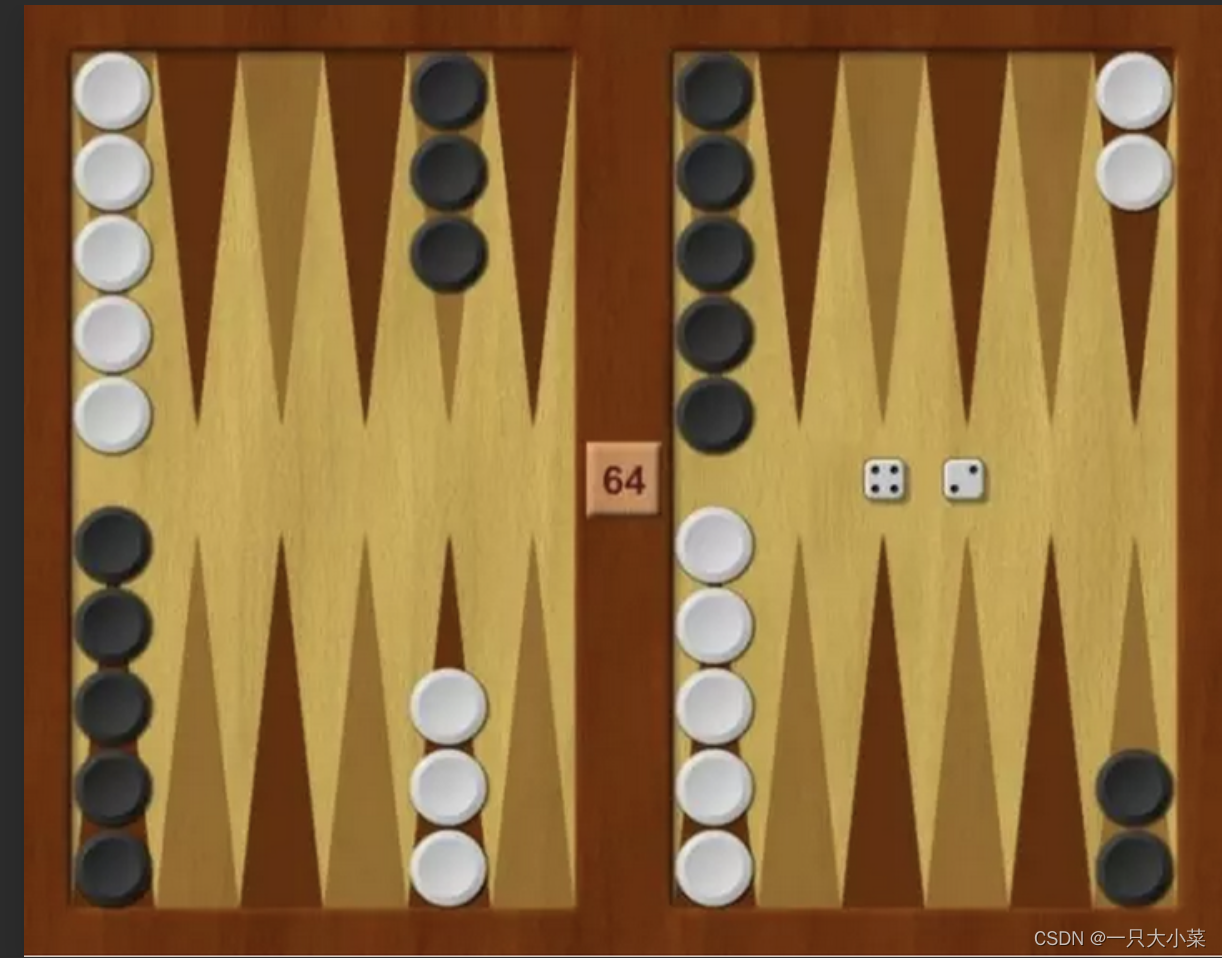
西洋双陆棋的博弈树中除了MAX和 MIN 结点之外还必须包括机会结点。在图 5.11 中机会结点用圆圈表示。每个机会结点的子结点代表可能的掷骰子结果;每个分支上标记着骰子数及其出现的概率。
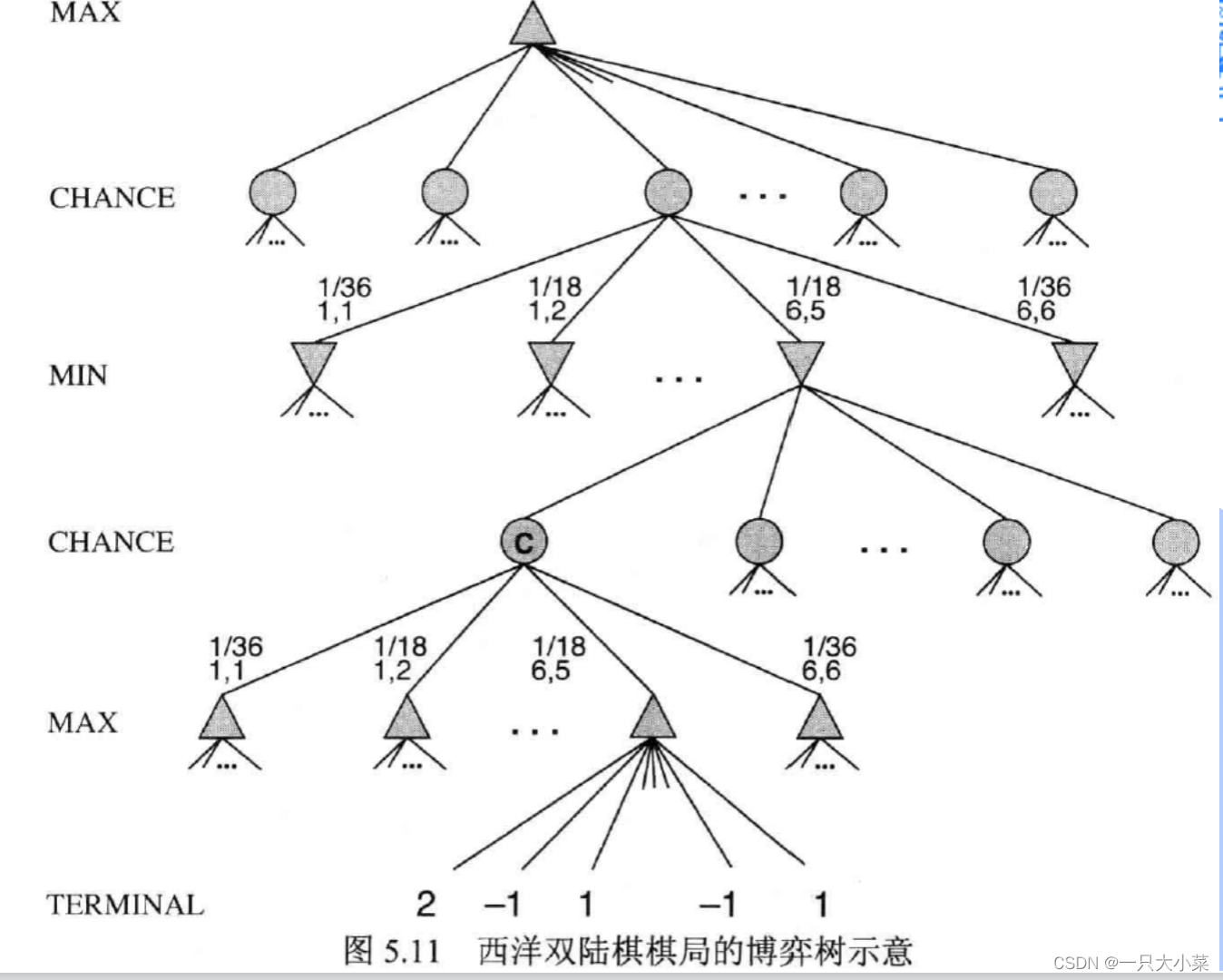
ExpectMinMax(s):
- U t i l i t y ( s ) , s 为终止状态 Utility(s),s为终止状态 Utility(s),s为终止状态
- M a x a E x p e c t M i n M a x ( R e s u l t ( s , a ) ) , s 为 M A X 结点 Max_{a}ExpectMinMax(Result(s,a)),s为MAX结点 MaxaExpectMinMax(Result(s,a)),s为MAX结点
- M i n a E x p e c t M i n M a x ( R e s u l t ( s , a ) ) , s 为 M I N 结点 Min_{a}ExpectMinMax(Result(s,a)),s为MIN结点 MinaExpectMinMax(Result(s,a)),s为MIN结点
- ∑ r P ( r ) E x p e c t M i n M a x ( R e s u l t ( s , r ) ) , s 为机会结点 ∑rP(r)ExpectMinMax(Result(s,r)),s为机会结点 ∑rP(r)ExpectMinMax(Result(s,r)),s为机会结点
本章小结
对抗搜索是一种解决竞争性环境下决策问题的搜索算法。传统的对抗搜索算法如Minimax和Alpha-Beta剪枝通过构建博弈树和回溯剪枝来找到最优决策。随机对抗搜索引入随机因素,考虑对手的随机行为,增加决策的多样性。实时对抗搜索针对实时决策问题,在有限时间内进行部分搜索并权衡时间和质量,以找到最佳决策。这些扩展形式使对抗搜索更加灵活和适应不同的竞争环境和需求,提供了更好的决策策略和性能优化。