《人工智能：一种现代方法》第17章复杂决策问题学习笔记

前言

本篇文章来自Artificial Intelligence: A Modern Approach一书第17章“复杂决策问题”，进行了翻译和整理，仅供学习参考。

正文

在之前的章节中讨论了单个决策问题，这些问题特点是行动带来的效用是完全知道的，而接下来讨论的序贯决策问题，效用取决于一序列的行动，而不是单个的行动。举个例子，就像下象棋一样，最后的输赢并不能够从一开始下的几步就可以预见到，只有当你最后输了或者赢了的时候，再回过头去分析自己走过的每一步，就会发现有哪几步走得不好，影响了后面几步，乃至决定了胜负。但是在下棋过程，你是不知道，也无法确定那几步就会决定胜负关系的。所以说下象棋的输赢取决于一系列的步数，而不是单个的下子。

17.1 序贯决策问题

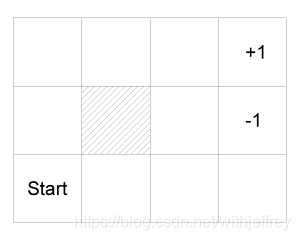
现在设定一个如上图所示的游戏，规则是智能体从Start位置开始，每步只能按照上下左右的动作走一格，当到达+1和-1时游戏结束，当智能体到达+1则表示赢得了游戏。如果智能体选择其中一种动作，而且该动作100%会执行或者说发生，那么很明显可以按照上上右右右或者右右上上上的顺序依次执行，达到+1。但是如果这是一个充满着“不确定”的世界，当智能体选择某一种动作时，只有80%的概率到达动作期望的状态，而20%的概率则是与所选择动作呈90°的方向到达另一个状态。比如说，从（1，1）开始，如果选择上，并且最终到达状态（1，2）的概率只有80%，而实际执行右并到达（2，1）有10%概率，实际执行左将碰到墙壁而保持不动有10%概率。我们用转换模型（Transition Model）来表示这样一组从一个状态因采取不同的动作到达另一个状态的概率模型。

现在我们来定义效用函数。定义一个动作序列的效用函数就是最后状态的效用减去0.04*动作序列的长度，也就是说，每一个除了+1和-1的状态，都有-0.04的“奖励”，而一系列的状态的奖励之和可以计算出其效用。比如说动作序列长度为6，那么一系列动作后到达+1，那么效用为0.76。在一个“确定”的世界，智能体在给定的动作下可以到达期望的状态，而在一个“不确定”的世界，智能体虽然给定了动作，但是有一定的概率达到期望的状态。比如说，智能体在（3，2），动作是（上，右），那么它到达（4，3）状态的概率是0.64。具体过程如下图所示：

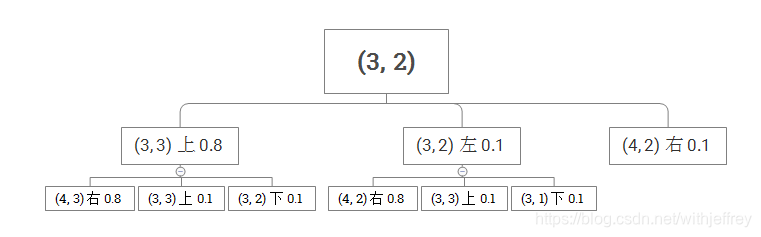
它可能到达的状态有5个：

• 到达（4，3）的概率为0.8*0.8=0.64
• 到达（3，3）的概率为0.8*0.1+0.1*0.1=0.09
• 到达（3，2）的概率为0.8*0.1=0.08
• 到达（4，2）的概率为0.1*0.8+0.1=0.18
• 到达（3，1）的概率为0.1*0.1=0.01

正好所有的概率之和为0.64+0.09+0.08+0.18+0.01=1

一个完整的从状态到动作的映射称之为策略。给定一个策略，可以计算出该策略的期望效用。所以，我们要解决的问题也就是计算出最佳的策略，即可以最大化期望效用的策略。这样一个理想和随机的世界，通过转换模型寻找最佳策略的问题称之为马可夫决策问题（MDP），以俄罗斯的统计学家Andrei A. Markov命名。马可夫属性是指任何一个状态的转换概率仅仅取决于当前该状态，而与之前的历史状态无关。

另外，如果是在一个非理想的环境中，智能体在感知时不能获取到足够的信息来描述其当前的状态以及转换概率。在运筹学领域，这样的问题被称为部分可观测马可夫决策问题（POMDP）。这一点暂时不展开。

17.2 值迭代

通过值迭代的算法来计算最佳策略。值迭代的基本思路是先计算每个状态的效用U(state)，然后根据效用选择每个状态的最佳行动。
首先需要定义每个状态的效用函数：
$R(i) = EU(H(i, policy*|M) = \sum P(H(i, policy*)|M)U_h(H(i, policy*)) \quad (17.1)$

这里的policy*是由转换模型M和序列U_h的效用决定的。这里的U_h要求符合可分割特性，该特性表明可以找到一个函数f使得U_h满足：
$U_h([s_0, s_1, ..., s_n]) = f(s_0, U_h([s_1, ..., s_n]))$
最简单的函数是加法：
$U_h([s_0, s_1, ..., s_n]) = R(s_0) + U_h([s1, ..., s_n]))$
这里的R是奖励函数。
给定Uh，可以进一步得到：
$policy^*(i) = \mathop {argmax}_{a} \sum_{j} M_{ij}^{a}U(j) \quad (17.2)$
$U(i) = R(i) + \mathop {max}_{a} \sum_{j} M_{ij}^{a} U(j) \quad (17.3)$
公式(17.3)是动态编程的基础，是解决序贯决策问题的一种解，由1950年末Richard Bellman发现。
反复地使用公式(17.3)，每一步都使用邻近状态的旧的效用估计值来更新状态的效用，可以得到下面的公式：
$U_{t+1} (i) \leftarrow R(i) + \mathop {max}_{a} \sum_j M_{ij}^{a} U_{t} (j) \quad (17.4)$
其中Ut(i)是在迭代t次后在状态i的效用估计值。随着t->∞，效用会收敛于一个稳定的值。这样一个算法称之为值迭代。

使用值迭代算法来计算在17.1一节介绍的游戏，那么它的最佳策略和状态效用为：

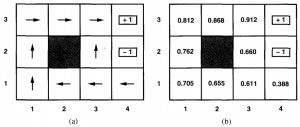
17.3 策略迭代
策略迭代算法是选择一个初始策略，然后计算在该策略下每一个状态的效用。然后通过下一个状态的效用来更新在每一个状态下的策略，直到策略达到稳定。在给定策略下决定效用的步骤被称之为value determination。

value determination算法可以通过以下两种方法表述：
第一种是简化版的值迭代，如下所示：
$U_{t+1} (i) \leftarrow R(i) + \sum_{j} M_{ij}^{Policy(i)} U_{t} (j)$
以及从策略迭代中获取的当前效用估计值作为初值值。

第二种是直接求解效用。给定策略P，状态的效用遵从以下一组等式：
$U(i) = R(i) + \sum_{j} M_{ij}^{P(i)} U_{t} (j)$
举个例子，假设P就是17.1提到的游戏的最佳策略，那么根据转换模型M，可以得到下面的等式：
$u_{(1,1)} = 0.8u_{(1,2)}+0.1u_{(1,1)}+0.1u_{(2,1)}$
$u_{(1,2)} = 0.8u_{(1,3)}+0.2u_{(1,2)}$
依次类推，最终可以得到包含有11个未知数的11个线性方程，并且可以通过高斯消元法进行求解。