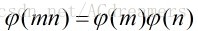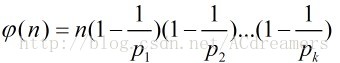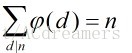先来介绍几个与欧拉函数有关的定理：
定理一：设m与n是互素的正整数，那么
定理二：当n为奇数时，有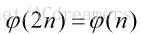
因为2n是偶数，偶数与偶数一定不互素，所以只考虑2n与小于它的奇数互素的情况，则恰好就等于n的欧拉函数值。
定理三：设p是素数，a是一个正整数，那么
关于这个定理的证明用到容斥：
由于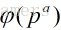
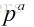
那么小于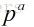
定理四：设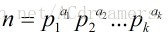
这个定理可以根据定理一和定理三证明，其实用到的就是容斥。如果对容斥熟悉，其实完全就可以直接容斥。
定理五：设n是一个正整数，那么
这个其实可以看莫比乌斯反演就明白了。
定理六：设m是正整数，(a,m)=1，则：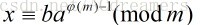
定理七：如果n大于2，那么n的欧拉函数值是偶数。
1.求单个数的欧拉函数（白书版本）
int euler_phi(int n){
int ans=n;
for(int i=2;i*i<=n;i++) if(n%i==0)
{
ans=ans/i*(i-1);
while(n%i==0) n/=i;
}
if(n>1) ans=ans/n*(n-1);
return ans;
}
}2.1求1~n中所有数的欧拉phi函数值（这里就不引用白书上的了，太慢了。。。）
void Solve(void)
{
for(int i=1; i<n; i++) p[i] = i;
for(int i=2; i<n; i+=2) p[i] >>= 1;
for(int i=3; i<n; i+=2)
{
if(p[i] == i)
{
for(int j=i; j<n; j+=i)
p[j] = p[j] - p[j] / i;
}
}
}算法原理：开始令i的欧拉函数值等于它本身，如果i为偶数，可以利用定理二变为求奇数的。若p是一个正整数满足
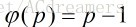，那么p是素数，在遍历过程中如果遇到欧拉函数值等于自身的情况，那么说明该数为素数。把这个数的欧拉函数值改变，同时也把能被该素因子整除的数改变。2.2 求1~n中欧拉函数的改进版（主要看n大不大）
先打个素数表：
bool isprime[n];
long long num_prime;
void get_prime(){
memset(isprime,true,sizeof(isprime));
isprime[0]=isprime[1]=false;
for(int i=2;i*i<n;i++){
if(isprime[i]){
num_prime++;
for(int j=i*i;j<=n;j+=i)
isprime[i]=false;
}
}
}对于任意一个能被n整除的质数，有m = n/p
当m%p == 0 的时候，phi(n) = phi(m)*p
当m%p != 0的时候，phi(n) = phi(m)*(p-1)
long long dp[n]= {0ll};
void Solve(void)
{
get_prime();
for(int i=2; i<n; ++i)
{
if(is_prime[i])
dp[i]=i-1;
else
{
for(int j=0; j<num_prime; ++j)
if(i%prime[j]==0)
{
if((i/prime[j])%prime[j]==0)
dp[i]=dp[i/prime[j]]*prime[j];
else
dp[i]=dp[i/prime[j]]*(prime[j]-1);
break;
}
}
}
}递推式证明：
1）由质因数分解定理得，在n中至少能够分解出一个素数p，导致 n = p*m，那么可以将1~n划分为一个区间的集合{ [m*(i-1) , m*i ] , 1<=i<=p }，则对于每个区间[m*(i-1)+1,m*i],其中的每个数可以看做m*(i-1)+j (1<=j<=m)。
2）所以gcd ( m*(i-1)+j , m )
= gcd ( m , (m*(i-1)+j)%m ) （根据秦九韶辗转相除法）
=gcd ( m , j )
那么也就是每个区间对应位置的数均与1~m中的某个数gcd相同，互质便是gcd(a,b)==1,所以1~n中与m互质的数有p*phi(m)个。
3）那么我们接下来进行分类讨论：
若m%p == 0 , 那么 m = a*p（a为一个正整数），所以若gcd(b,m) == 1 ,那么 gcd ( b , p ) == 1 , 所以 gcd ( m*p , b ) == 1 , 即gcd ( n , b ) == 1 ,所以在这种情况与m互质的数均与n互质,所以phi(n) = phi(m)*p;
若m%p != 0 , 那么若gcd ( b , m) == 1 , gcd ( b , p ) == p , 那么 gcd ( n , b ) == p,所以1~m与m互质的数为q,若m%p != 0 , 那么与m互质且与p不互质的数是q*p，因此在n当中这样的数有phi(m)个，所以 phi(n) = phi(m)*p - phi(m)
例题：POJ 2478
题意：输入n，求n以内的数的欧拉函数的和（分子分母互素）2.1版：422MS
#include <stdio.h>
#include <iostream>
#include <cstring>
using namespace std;
const int MAX=1000010;
int prime[MAX]={0},num_prime=0;//num_pirme记录素数个数
bool is_prime[MAX];
void GetPrime()
{
memset(is_prime,true,sizeof(is_prime));
is_prime[0]=is_prime[1]=false;
for(int i=2;i*i<MAX;i++)
{
if(is_prime[i])
for(int j=i*i;j<=MAX;j+=i)
{
is_prime[j]=false;
}
}
}
long long p[MAX];
void Solve()
{
for(int i=1; i<MAX; i++) p[i] = i;
for(int i=2; i<MAX; i+=2) p[i] >>= 1;
for(int i=3; i<MAX; i+=2)
{
if(p[i] == i)
{
for(int j=i; j<MAX; j+=i)
p[j] = p[j] - p[j] / i;
}
}
}
int main(void)
{
int n,ncase=1;
Solve();
while(scanf("%d",&n)==1 && n)
{
long long sum=0;
for(int i=2;i<=n;i++){
sum+=p[i];
}
cout<<sum<<endl;
}
return 0;
}
2.2版：157MS
#include <cstdio>
#include <iostream>
#include <cstring>
using namespace std
const int maxn=1000010;
int prime[maxn],num_prime=0;//num_pirme记录素数个数
bool is_prime[maxn];
void get_Prime()
{
memset(is_prime,true,sizeof(is_prime));
is_prime[0]=is_prime[1]=false;
for(int i=2;i*i<maxn;i++)
{
if(is_prime[i])
prime[num_prime++]=i;
for(int j=i*i;j<=maxn;j+=i)
{
is_prime[j]=false;
}
}
}
long long dp[maxn]={0ll};
void solve()
{
get_Prime();
for(int i=2;i<maxn;++i)
{
if(is_prime[i])
dp[i]=i-1;
else
{
for(int j=0;j<num_prime;++j)
if(i%prime[j]==0)
{
if((i/prime[j])%prime[j]==0)
dp[i]=dp[i/prime[j]]*prime[j];
else
dp[i]=dp[i/prime[j]]*(prime[j]-1);
break;
}
}
}
for(int i=3;i<maxn;++i)
dp[i]+=dp[i-1];
}
int main(void)
{
int n;
solve();
while(scanf("%d",&n)==1 && n)
{
printf("%lld\n",dp[n]);
}
return 0;
}借鉴了两篇别人的文章：