数据结构与算法分析——第七章 排序

7.1 预备知识

     1，算法接收 含元素的数组和包含元素个数的整数

     2，基于比较的排序

7.2 插入排序

     代码实现

void InsertionSort(ElementType A[],int N)
{
    int i,j;
    ElementType Tmp;
    for(i = 1 ; i < N ; i++)
    {
        Tmp = A[i];
        for(j = i ; j > 0 && A[j - 1] > Tmp ; j--)
        {
            A[j] = A[j - 1];
        }
        A[j] = Tmp;//避免明显使用交换
    }
}

　　理解描述

　　位置i上元素存于Tmp中，i之前所有更大的元素向右移一位（i前所有元素已排序），Tmp被置于正确位置。

　　分析

　　1，（未排序）嵌套循环每个花费N次迭代，为O(N^2)

　　2，（已排序）为O(N)

　　*由于差距较大，故值得分析平均情形

 

7.3 一些简单排序算法的下界

　　1，怎样概括“一些”的共性？ 　     

       引入逆序 —— 插排交换次数=逆序数（O(N) <=> O(N + I),N:其他工作，I:逆序数）—— 平均运行时间 <=> 平均逆序数

       * 以插排为例分析（插排 代表 通过交换相邻元素进行排序的算法），得出共性

　　2，结论

　    定理7.1  N个互异数的数组的平均逆序数是N(N-1)/4

　　定理7.2  通过交换相邻元素进行排序的任何算法平均需要Ω(N^2)时间

7.4 希尔排序

　　代码实现

void ShellSort(ElementType A[],int N)
{
    int i,j,Increment;
    ElementType Tmp;
    for(Increment = N / 2 ; Increment > 0 ; Increment /= 2)
    {
        for(i = Increment ; i < N ; i++)//小型插排
        {
            Tmp = A[i];
            for(j = i ; j >= Increment && A[j - Increment] > Tmp ; j -= Increment)
            {
                A[j] = A[j - Increment];
            }
            A[j] = Tmp;
        }
    }
}

　　理解描述

　　不断缩小增量的插入排序，通过远距离交换以达到一次消除多对逆序（需保证增量变换时不干扰已处理的顺序），减小每一趟工作量，即亚二次运行时间。

　　分析

　　定理7.3  使用希尔增量的希尔排序的最坏运行时间为Θ(N^2)

　　定理7.4  使用 Hibbard 增量的希尔排序的最坏运行时间为Θ(N^2)  (Hibbard增量形如 1,3,7,...,2^k - 1)

7.5 堆排序

　　代码实现

#define LeftChild(i) (2 * (i) + 1)//下标从0开始,因此为 2*i+1
void PercDown(ElementType A[],int i,int N)
{
    int Child;
    ElementType Tmp;
    for(Tmp = A[i] ; LeftChild(i) < N ; i = Child)//下标从0开始,注意边界
    {
        Child = LeftChild(i);
        if(Child != N - 1 && A[Child + 1] > A[Child])//Child != N - 1 即右边还有数据
        {
            Child++;//选出较大的儿子
        }
        if(Tmp < A[Child])
        {
            A[i] = A[Child];
        }
        else
        {
            break;
        }
    }
    A[i] = Tmp;
}
void HeapSort(ElementType A[] , int N)
{
    int i;
    //BuildHeap
    for(i = N / 2 ; i >= 0 ; i--)//从右向左,从下向上,逐步下滤
    {
        PercDown(A,i,N);
    }
    //DeleteMax
    for(i = N - 1 ; i > 0 ; i--)
    {
        Swap(&A[0] , &A[i]);
        PercDown(A , 0 , i);//位置0处元素下滤,且元素个数改变

    }
}

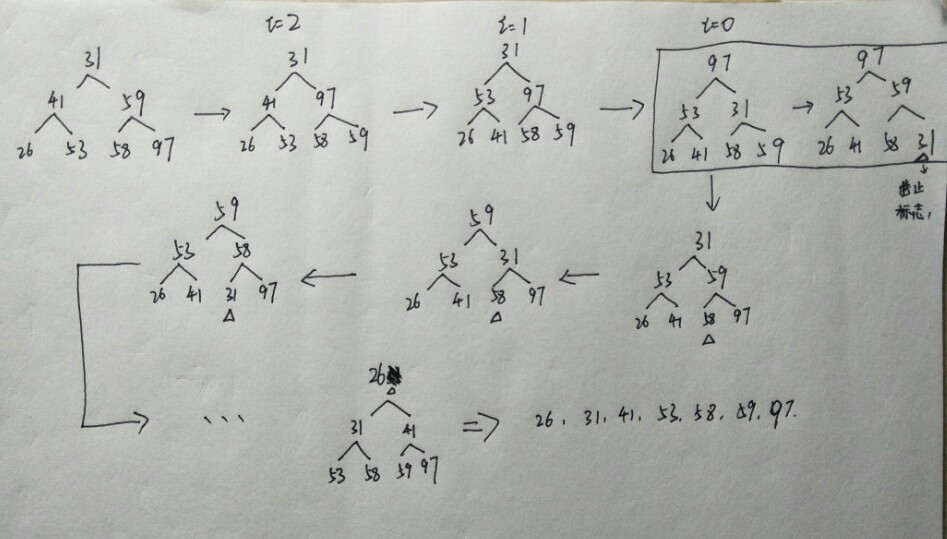
上图为构建初始堆及排序过程，数组中表,97.58,31,26,41,58,31　　

　　理解描述

　　1，对已有数组元素进行整理，构建max堆（max堆便于实施从小到大排序）

　　2，排序时通过回收利用空间，避免使用第二个数组

　　分析

　　定理7.5  对N个互异项的随机排列进行堆排序，所用的平均比较次数为 2NlogN - O(NlogN)

7.6归并排序

　　代码实现

void MergeSort(ElementType A[],int N)//驱动例程
{
    ElementType *TmpArray;
    TmpArray = malloc(N * sizeof(ElementType));
    if(TmpArray != NULL)
    {
        MSort(A,TmpArray,0,N - 1);
        free(TmpArray);
    }
    else
    {
        FatalError("No space for tmp array");
    }
}
void MSort(ElementType A[],ElementType TmpArray[],int Left,int Right)
{
    int Center;
    if(Left < Right)//条件成立时再对Center赋值
    {
        Center = (Left + Right) / 2;
        MSort(A , TmpArray , Left , Center);
        MSort(A , TmpArray , Center + 1 , Right);
        Merge(A , TmpArray , Left , Center + 1 , Right);//Center + 1 即右半部分始位置
    }
}
void Merge(ElementType A[] , ElementType TmpArray[] , int Lpos , int Rpos , int RightEnd)
{
    int i , LeftEnd , TmpPos , NumElements;
    //NumElements 存放每次排序时元素总数(临时数组元素转移至原数组时使用)
    //TmpPos 记录排序元素在新建数组中*对应*位置
    
    LeftEnd = Rpos - 1;
    NumElements = RightEnd - Lpos;
    TmpPos = Lpos;
    
    while(Lpos < LeftEnd && Rpos < RightEnd)
    {
        if(A[Lpos] < A[Rpos])
        {
            TmpArray[TmpPos++] = A[Lpos++];
        }
        else
        {
            TmpArray[TmpPos++] = A[Rpos++];
        }
    }
    
    //Copy rest of each half
    while(Lpos <= LeftEnd)
    {
        TmpArray[TmpPos++] = A[Lpos++];
    }
    while(Rpos <= RightEnd)
    {
        TmpArray[TmpPos++] = A[Rpos++];
    }
    
    for(i = 0 ; i < NumElements ; i++ , RightEnd--)
    {
        A[RightEnd] = TmpArray[RightEnd];
    }
}

　　理解描述

　　1，递归是怎样实施的？

　　答：以8个元素为例，左右各分成4 个元素，先处理左边4 个，将左边4个元素重复分隔，直到左边只剩一个元素，达到基准条件，返回最近主程序中，处理右边一个元素，达到基准条件，进行合并，此时这两个元素作为左侧，返回最近主程序中，处理右边两个元素，继续先左后右，处理合并，返回最近主程序中，进行合并。此时总体来看，8个元素，左侧4个已实施“分治”，接下来继续进行递推，过程类似。

　　2，小块元素合并后怎样存放？

　　答：小块元素在临时数组*对应位置*进行合并存放，排序后依次放入原数组中，不影响后面元素及其排序。

　　分析　

　　运行时间：T(N) = O(NlogN)

　　应用：很难用于主存排序。首先，合并两个线性表需要线性附加内存，其次，数据在数组间拷贝需要时间。　

7.7 快速排序

　　代码实现

//驱动例程
void QuickSort(ElementType A[] , int N)
{
    QSort(A , 0 , N - 1);
}

//选取枢纽元
//对三元素排序，最值放两边，枢纽元置于 right-1 处(此方法便于设置警戒标志，防止越界)
ElementType Median3(ElementType A[] , Left , Right)
{
    int Center;
    Center = (Left + Right) / 2;
    if(A[Left] > A[Center])
    {
        Swap(&A[Left] , &A[Center]);
    }
    if(A[Left] > A[Right])
    {
        Swap(&A[Left] , &A[Right]);
    }
    if(A[Center] > A[Right])
    {
        Swap(&A[Center] , &A[Right]);
    }
    Swap(&A[Center] , &A[Right - 1]);
    return A[Right - 1];
}

#define Cutoff (3)
void QSort(ElementType A[] , int Left , int Right)
{
    int i , j;
    ElementType Pivot;
    if(Left + Cutoff <= Right)//数组内大于3个元素时，分割加递归
    {
        Pivot = Median3(A , Left , Right);
        i = Left;//因为下方使用的是前自增
        j = Right - 1;
        for( ; ; )
        {
            while(A[++i] < Pivot){}
            while(A[--j] > Pivot){}
            if(i < j)
            {
                Swap(&A[i],&A[j]);
            }
            else
            {
                break;
            }
        }
        Swap(&A[i],&A[Right - 1]);//Restore pivot
        QSort(A , Left , i - 1);
        QSort(A , i + 1 , Right);
    }
    else
    {
       InsertionSort(A + Left , Right - Left + 1); 
    }
}

　　理解描述

　　与归并排序类似，区别是选取枢纽元，以枢纽元为界分割为大小两数组。（适用于大数组）

　　选取枢纽元：随机选取；三数中值分割法（左，右，中心位置里的中值,同时将三元素排序，便于设置警戒标志，防止越界）

　　分割策略：1，枢纽元与位置right - 1处元素互换

　　　　　　    2，设置i（left）,j（right - 1），i 向右滑动直至 i 处元素 >= 枢纽元，j 向左滑动直至 j 处元素 <= 枢纽元，交换i，j处元素

　　　　　　    3，i，j交错时，i 处元素与枢纽元交换

　　分析

　　最坏情况分析：枢纽元始终为最小元素，T(N) = O(N^2)

　　最好情况分析：枢纽元位于中间，T(N) = O(NlogN)

　　平均情况分析：每个文件大小等可能，求出平均分布，T(N) = O(NlogN)

　　扩展（选择问题的线性期望时间算法）

　　选择问题：查找集合S中第k个最小元

　　与快速排序类似，区别在于分割后，若 k <= |S1|,则返回quickselect( S1 , k )，若k = |S1| + 1 ，则枢纽元即为所求，否则返回quickselect(S2 , k - |S1| - 1)

　　代码实现

#define Cutoff (3)
void QuickSelect(ElementType A[] , int k , int N)
{
    QSelect(A , k , 0 , N - 1);
}

ElementType Median3(ElementType A[] , Left , Right)
{
    int Center;
    Center = (Left + Right) / 2;
    if(A[Left] > A[Center])
    {
        Swap(&A[Left] , &A[Center]);
    }
    if(A[Left] > A[Right])
    {
        Swap(&A[Left] , &A[Right]);
    }
    if(A[Center] > A[Right])
    {
        Swap(&A[Center] , &A[Right]);
    }
    Swap(&A[Center] , &A[Right - 1]);
    return A[Right - 1];
}

//位置k - 1处即为第k个最小值
void QSelect(ElementType A[] , int k , int Left , int Right)
{
    int i , j;
    ElementType Pivot;
    if(Left + Cutoff <= Right)
    {
        Pivot = Median3(A , Left , Right);
        i = Left;
        j = Right - 1;
        for( ; ; )
        {
            while(A[++i] < Pivot){}
            while(A[--j] > Pivot){}
            if(i < j)
            {
                Swap(&A[i],&A[j]);
            }
            else
            {
                break;
            }
        }
        Swap(&A[i],&A[Right - 1]);//Restore pivot
        if(k <= i)
        {
            QSelect(A , k , Left , i - 1);
        }
        else if(k > i + 1)
        {
            QSelect(A , k - i - 1 , i + 1 , Right);
        }
    }
    else
    {
       InsertionSort(A + Left , Right - Left + 1);
    }
}

7.8 大型结构的排序

　　排序时交换整个结构代价是昂贵的，解决办法是让输入数组包含指向结构的指针，通过指针比较关键字，必要时交换指针来进行排序。

7.9 排序的一般下界

　　引入决策树，通过只使用比较进行排序的每一种算法都可以用决策树表示。

　　引理7.1：令T是深度为d的二叉树，则T最多有2^d个树叶

　　引理7.2：具有L片树叶的二叉树深度至少是[ logL ]

　　定理7.6：只使用元素间比较的任何排序算法在最坏情况下至少需要[ log( N! ) ]次比较

　　定理7.7：只使用元素间比较的任何排序算法需要进行Ω(NlogN)次比较

7.10 桶式排序

　　以线性时间进行排序，构建数组，大小包含所有待排元素，初始为0，元素出现以1代替。

7.11 外部排序

　　简单算法（该部分内容转自@Judy518）——二路合并

　　例如要对外存中4500个记录进行归并，而内存大小只能容纳750个记录，在第一阶段，我们可以每次读取750个记录进行排序，这样可以分六次读取，进行排序，可以得到六　个有序的归并段，如下图：

　　

每个归并段的大小是750个记录，记住，这些归并段已经全部写到临时缓冲区（由一个可用的磁盘充当）内了，这是第一步的排序结果。

1、将内存空间划分为三份，每份大小250个记录，其中两个用作输入缓冲区，另外一个用作输出缓冲区。首先对Segment_1和Segment_2进行归并，先从每个归并段中读取250个记录到输入缓冲区，对其归并，归并结果放到输出缓冲区，当输出缓冲区满后，将其写道临时缓冲区内，如果某个输入缓冲区空了，则从相应的归并段中再读取250个记录进行继续归并，反复以上步骤，直至Segment_1和Segment_2全都排好序，形成一个大小为1500的记录，然后对Segment_3和Segment_4、Segment_5和Segment_6进行同样的操作。

2、对归并好的大小为1500的记录进行如同步骤1一样的操作，进行继续排序，直至最后形成大小为4500的归并段，至此，排序结束。

　　多路合并

　　1，2-路合并扩充为k-路合并，区别在于寻找k个元素中最小元过程稍微复杂，可通过优先队列寻找最小元，进行DeleteMin操作，得到下一个写到磁盘上的元素

　　2，在初始顺串构造阶段之后，k-路合并所需趟数为[ logk( N / M ) ]。（N为数据总量，M为内存容量）

　　多相合并

　　k-路合并需要2k盘磁带，然而使用 k + 1 盘磁带也有可能完成排序工作，作为例子，这里阐述只用三盘磁带（T1,T2,T3）如何完成2-路合并。

　　假设T1上有一个输入文件，它将产生34个顺串。

　　选择一：每盘磁带存入17个，然后合并存放至T1，再将T1前个8顺串存至T2，再次合并存至T3，依次类推。这样每一趟合并附加额外半趟工作。

　　选择二：将34个顺串不均衡地分成2份，例如21,13，再次进行合并。此时需考虑顺串最初的分配，事实上，若初始顺串为斐波那契数，则将其分裂为2个斐波那契数之和，否则需添加哑顺串填补磁带，将其补足为斐波那契数

　　替换选择（该部分内容转自@kph_Hajash）　　

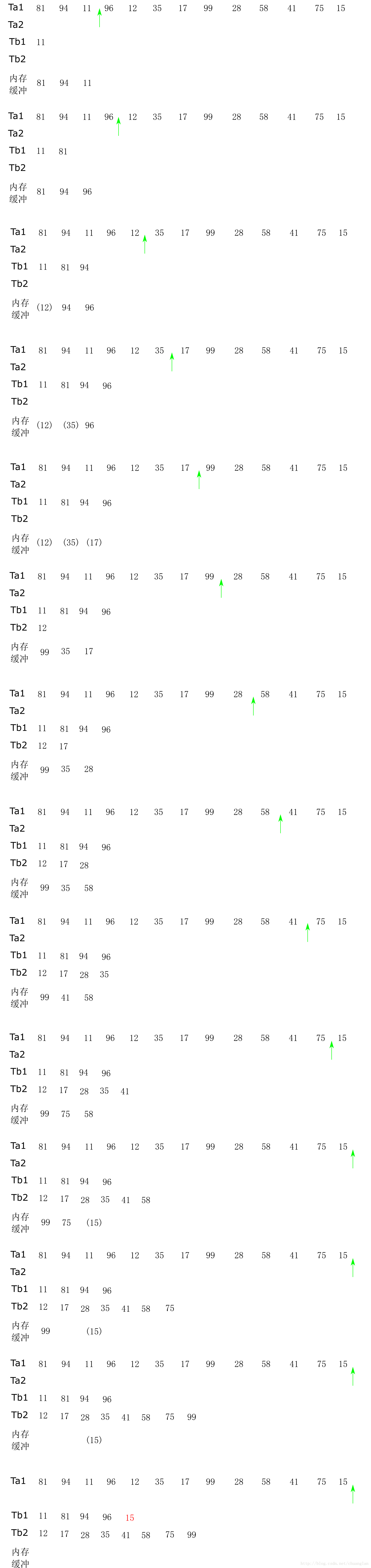
　　在标准的外排中，一次读入内存可容纳的 M 个记录，排序完依次输出到空磁带上；但这里其实有个小技巧，排完序后输出第一个记录到磁带上时，内存让出了一个记录的空间，这时我们可以从输入磁带取出一个记录，判断它是否大于刚输出的记录，若是，说明它可以放入当前顺串中（顺串是从小到大有序），否则，应暂存内存，等下一个顺串的构造； 这里暂存内存书上讲是放在最小堆的死区（dead space）。

初始顺串的构造详解，绿色箭头表示当前输入状态，Tbn 表示输出状态，内存缓冲表示当前内存中存在的记录（括号内记录表示存在最小堆的死区） 

从上图可知，与标准顺串构造方式生成的 5 个顺串相比，替换选择构造的初始顺串记录数更多，顺串数更少，只有 3 个，且前者需要 12 趟完成排序，替换选择只需 3 趟。