4. 松弛向量与软间隔
前面讨论的情况都是样本分布都可以被超平面完美分割的情况,但是在现实任务中,经常会有难以完美划分的情况,就算正好完美划分了样本点,也很难判断这个结果是不是过拟合造成的。
(图来自https://blog.csdn.net/zouxy09/article/details/17291543)
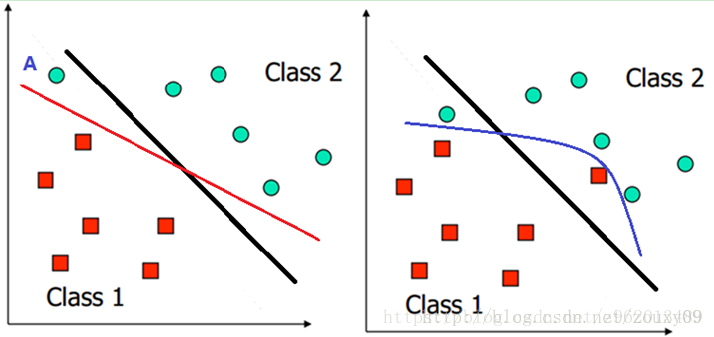
上左图中如果我们要考虑点A,得到的超平面就是红线那样,上右图中若是要考虑在class2中的红点,得到的超平面就是蓝线那样,如此精确的划分每个点很容易导致模型过拟合,为了缓解这个问题,我们引入软间隔的概念,软间隔允许某些样本不满足约束:
yi(ωTxi+b)≥1(4.1)
于是我们修改了优化目标:
min.12∥ω∥2+C∑i=1ml0/1(yi(ωTxi+b)−1)(4.2)
其中C>0是一个常数,
l0/1(z)
是“0/1损失函数”
l0/1(z)={1,0,if z<0otherwise
当C无穷大时,式(4.2)后面的部分迫使所有样本均满足式(4.1)的约束条件,式(4.2)则等价于(1.2),也就是说C越大,拟合非线性的能力越强,同时过拟合的风险也越高。引入
l0/1(z)
的目的是,我们只希望那些不满足(4.1)约束条件的点被算入优化目标中,但是
l0/1(z)
非凸,非连续,导致这样的目标函数不容易求解,我们可以使用近似的曲线替代,常用的损失函数为hinge函数:
lhinge(z)=max(0,1−z)
若采用hinge损失函数,则式(4.2)变成了:
min.12∥ω∥2+C∑i=1mmax(0,1−yi(ωTxi+b))(4.3)
引入松弛变量
ξi≥0
后,原来的约束条件就变为:
{yi(ωTxi+b)≥1−ξiξi≥0(4.4)
同时式(4.3)也可以改写为
min.12∥ω∥2+C∑i=1mξi(4.5)
我们重新引入拉格朗日乘子
αi≥0 i=1,2,...,m
,可得:
L(ω,b,α,ξ,β)=12∥ω∥2+C∑i=1mξi+∑i=1mαi(1−ξi+yi(ωTφ(xi)+b))−∑i=1mβiξi
对
ω,b,ξi
分别求偏导,得:
⎧⎩⎨⎪⎪ω=∑mi=1αiyiφ(xi)0=∑mi=1αiyiC=αi+βi
将结果带入原式得对偶问题:
max.∑i=1mαi−12∑i=1,y=1mαiαjyiyjκ(xi,xj)s.t. ∑i=1mαiyi=0 0≤αi≤C(4.6)
和前面说的KKT条件类似,这个对偶问题同样需要满足以下KKT条件:
⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪αi≥0yif(xi)−1+ξi≥0αi(yif(xi)−1+ξi)=0ξi≥0βi≥0βiξi=0(4.7)
5. SMO算法
SMO(Sequential Minimal Optimization)被用来求解SVM问题,该算法的思想是先固定
αi
以外的参数,然后求
αi
上的极值,由于存在(4.6)中的约束,我们可以先固定2个变量
αi
和
αj
,然后利用约束条件
∑mi=1αiyi=0
可以用
αi
代表
αj
,然后更新
αi
和
αj
,再重新选择2个参数,直到收敛。
注意到只需选取的
αi
和
αj
中有一个不满足KKT(4.7)条件,目标函数(4.6)就会在迭代后变大,因此我们要根据KKT条件来选择要更新的
αi
和
αj
,下面我们分析一下如何选取:
- 当
αi=0
时,
βi=C
,则
ξi=0
,得
yif(xi)≥1
- 当
αi=C
时,
βi=0
,则
ξi≥0
,且
yif(xi)−1+ξi=0
,得
yif(xi)≤1
- 当
0<αi<C
时,
0<βi<C
,则
ξi=0
,且
yif(xi)−1+ξi=0
,得
yif(xi)=1
我们在编程时只需要选择的
αi
对应的
yi,xi
违背上面的约束就可以让目标函数变大。
假如我们根据违背KKT条件选择了
α1,α2
,则:
y1α1+y2α2=NN=−∑i≠1,2myiαi(5.1)
因为
yiyi=1
,则有:
α1=Ny1−y1y2α2(5.2)
将
αi
和
αj
代入式(4.6),得:
W(α1,α2)=α1+α2−12α21y21κ11−12α22y22κ22−∑i=3mα1αiy1yiκ(1,i)−∑i=3mα2αiy2yiκ(2,i)+C(5.3)
C为一些常数的和
我们令
v1=∑mi=3α1αiy1yiκ(1,i)
,
v2=∑mi=3α2αiy2yiκ(2,i)
,则式(5.3)改为:
W(α1,α2)=α1+α2−12α21y21κ11−12α22y22κ22−α1y1v1−α2y2v2+C
代入式(5.2)得
W(α2)=−12y21(Ny1−y1y2α2)2κ1,1−12α22y22κ2,2−(Ny1−y1y2α2)α2y1y2κ1,2−(Ny1−y1y2α2)y1v1−α2y2v2+α1+α2+C=−12(N−y2α2)2κ1,2−12α22κ1,2−(y2Nα2−α22)κ1,2−(N−y2α2)v1−α2y2v2+Ny1−y1y2α2+α2+C(5.4)
对(5.4)求导得0:
∂W(α2)∂α2=Ny2κ1,1−α2κ1,1−α2k2,2−y2Nκ1,2+2α2κ1,2+y2v1−y2v2−y1y2+1=−(κ1,1+κ2,2−2κ1,2)α2+κ1,1Ny2−κ1,2Ny2+v1y2−v2y2−y1y2+1=0(5.5)
由于
f(x)=∑mi=1αiyiκ(xi,x)+b
,则有:
v1=∑i=3mαiyiκi,1=f(x1)−αold1y1κ1,1−αold2y2κ1,2−bv2=f(x2)−αold1y1κ1,2−αold2y2κ2,2−b
又因为
αold1=(N−αold2y2)y1
,则:
v1−v2=f(x1)−f(x2)−κ1,1N+κ1,2N+(κ1,1+κ2,2−2κ1,2)αold2y2
代入(5.5):
∂W(α2)∂α2=−(κ1,1+κ2,2−2κ1,2)αnew2+(κ1,1+κ2,2−2κ1,2)αold2+y2(y2−y1+f(x1)−f(x2))(5.6)
令
η=κ1,1+κ2,2−2κ1,2
,
E=f(x)−y
,则:
∂W(α2)∂α2=−ηαnew2+ηαold2+y2(E2−E1)=0
αnew2=αold2+y2(E1−E2)η(5.7)
这样我们就获得了新的
α2
值,但是不要忘记,
α
是存在约束的:
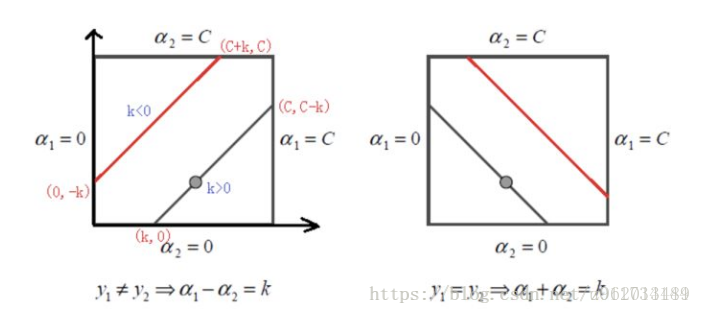
0≤α≤C
(图来自
https://blog.csdn.net/u011734144/article/details/81233553)
当
y1≠y2
时
α2
的上下界为:
- 下界:
L=max(0,αold2−αold1)
- 上界:
H=min(C,C+αold2−αold1)
当
y1=y2
时
α2
的上下界为:
- 下界:
L=max(0,αold1+αold2−C)
- 上界:
H=max(C,αold1+αold2)
这样我们就能获得约束后的
αnew2
αnew/constraint2=⎧⎩⎨⎪⎪Hαnew2Lαnew2>HL≤αnew2≤Hαnew2<L
然后我们就可以根据
αold1y1+αold2y2=αnew1y1+αnew2y2
计算
αnew1
了:
αnew1=alphaold1+y1y2(alphaold2−alphanew2)
未完待续

