Python 支持向量机 SVM

$\qquad$ 支持向量机简称SVM，是Support Vector Machine 的缩写。SVM是一种分类算法，在工业界和学术界都有广泛的应用，特别是针对数据集较小的情况下，往往其分类效果比神经网络好。

算法原理

$\qquad$ SVM的最大特点是能构造出最大间距的决策边界，从而提高分类算法的鲁棒性。

大间距分类算法

$\qquad$ 假设要对一个数据集进行分类，如图1所示，可以构造一个分割线把圆形的点和方形的点分开。这个分割线称为分割超平面（Separating hyperplane）。
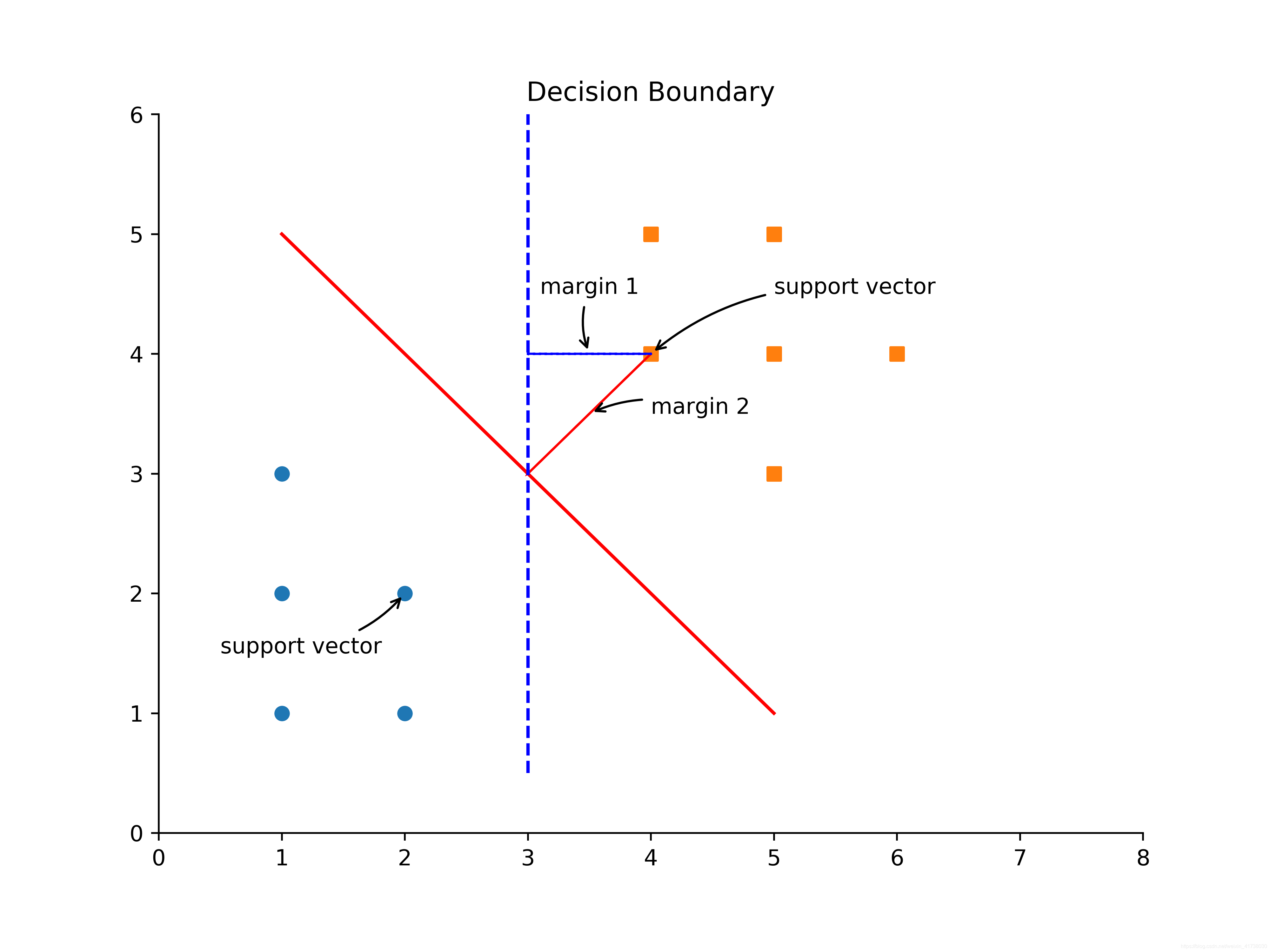
在这里插入图片描述
$\qquad$ 图1可视化图Python代码：

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
class1 = np.array([[1, 1], [1, 3], [2, 1], [1, 2], [2, 2]])
class2 = np.array([[4, 4], [5, 5], [5, 4], [5, 3], [4, 5], [6, 4]])
plt.figure(figsize=(8, 6), dpi=144)

plt.title('Decision Boundary')

plt.xlim(0, 8)
plt.ylim(0, 6)
ax = plt.gca()                                  # gca 代表当前坐标轴，即 'get current axis'
ax.spines['right'].set_color('none')            # 隐藏坐标轴
ax.spines['top'].set_color('none')

plt.scatter(class1[:, 0], class1[:, 1], marker='o')
plt.scatter(class2[:, 0], class2[:, 1], marker='s')
plt.plot([1, 5], [5, 1], '-r')
plt.arrow(4, 4, -1, -1, shape='full', color='r')
plt.plot([3, 3], [0.5, 6], '--b')
plt.arrow(4, 4, -1, 0, shape='full', color='b', linestyle='--')
plt.annotate(r'margin 1',
             xy=(3.5, 4), xycoords='data',
             xytext=(3.1, 4.5), fontsize=10,
             arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2"))
plt.annotate(r'margin 2',
             xy=(3.5, 3.5), xycoords='data',
             xytext=(4, 3.5), fontsize=10,
             arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2"))
plt.annotate(r'support vector',
             xy=(4, 4), xycoords='data',
             xytext=(5, 4.5), fontsize=10,
             arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2"))
plt.annotate(r'support vector',
             xy=(2, 2), xycoords='data',
             xytext=(0.5, 1.5), fontsize=10,
             arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2"))

$\qquad$ 从图1可以明显看出，实现的分割线比虚线的分割线更好，因为使用实现的分割线进行分类时，离分割线最近的点到分割线上的距离更大，即margin2 > margin1。这段距离的两倍，称为间距（margin）。那些离分隔超平面最近的点，称为支持向量（support vector）。为了达到最好的分类效果，SVM的算法原理就是要找到一个分隔超平面，它能把数据集正确地分类，并且间距最大。
$\qquad$ 首先，我们来看怎么计算间距。在二维空间里，我们使用方程 $w_1x_1+w_2x_2+b=0$ 来表示分隔超平面。针对高纬度空间，可写成一般化的向量形式，即 $w^Tx+b=0$ 。我们画出与分割超平面平行的两条直线，分别穿过两个类别的支持向量（离分隔超平面距离最近的点）。这两条直线的方程分别为 $w^Tx+b=-1$ 和 $w^Tx+b=1$ ，如图2所示。

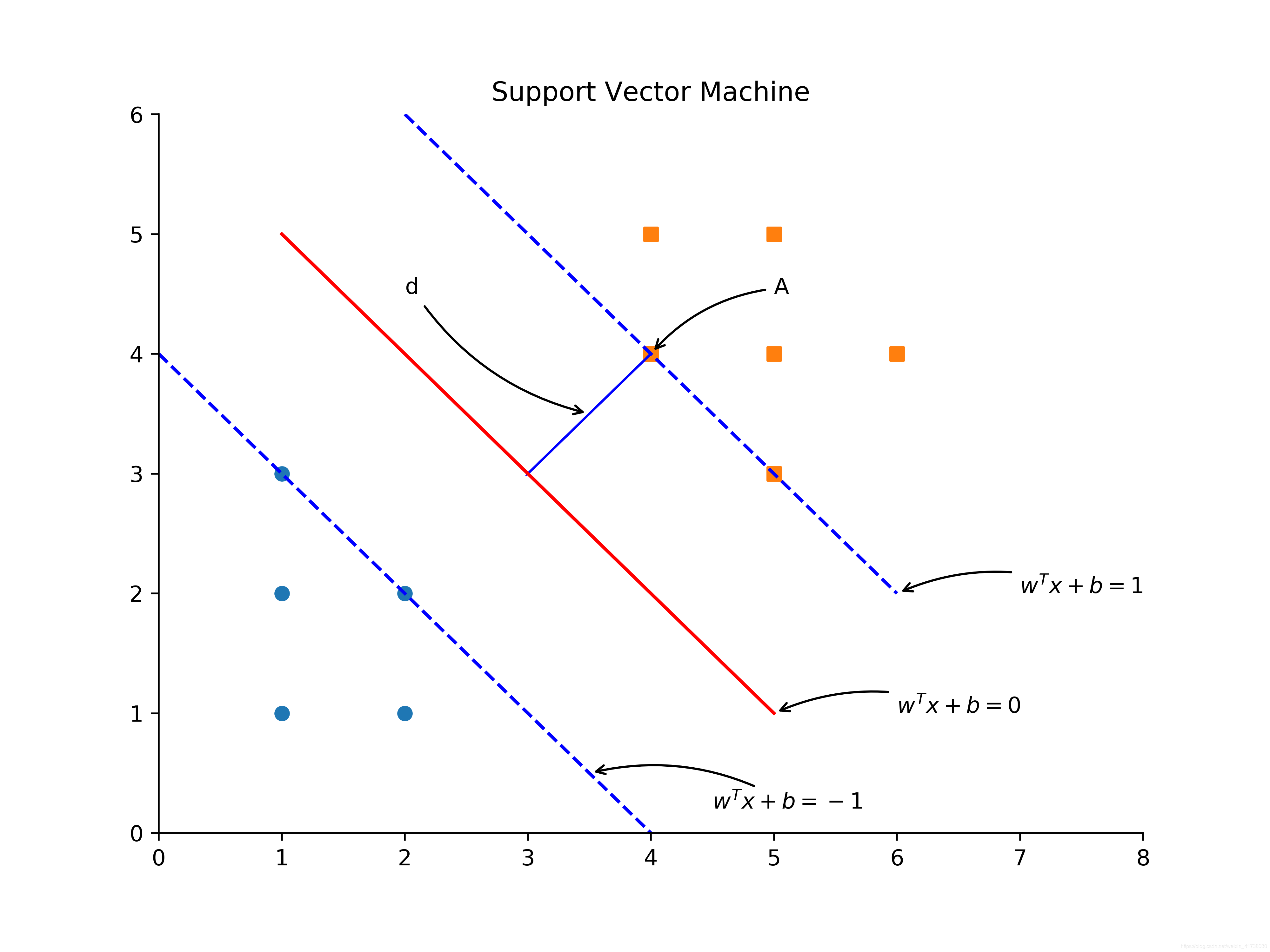
$\qquad$ 图2的可视化图Python代码：

plt.figure(figsize=(8, 6), dpi=144)

plt.title('Support Vector Machine')

plt.xlim(0, 8)
plt.ylim(0, 6)
ax = plt.gca()                                  # gca 代表当前坐标轴，即 'get current axis'
ax.spines['right'].set_color('none')            # 隐藏坐标轴
ax.spines['top'].set_color('none')

plt.scatter(class1[:, 0], class1[:, 1], marker='o')
plt.scatter(class2[:, 0], class2[:, 1], marker='s')
plt.plot([1, 5], [5, 1], '-r')
plt.plot([0, 4], [4, 0], '--b', [2, 6], [6, 2], '--b')
plt.arrow(4, 4, -1, -1, shape='full', color='b')
plt.annotate(r'$w^T x + b = 0$',
             xy=(5, 1), xycoords='data',
             xytext=(6, 1), fontsize=10,
             arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2"))
plt.annotate(r'$w^T x + b = 1$',
             xy=(6, 2), xycoords='data',
             xytext=(7, 2), fontsize=10,
             arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2"))
plt.annotate(r'$w^T x + b = -1$',
             xy=(3.5, 0.5), xycoords='data',
             xytext=(4.5, 0.2), fontsize=10,
             arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2"))
plt.annotate(r'd',
             xy=(3.5, 3.5), xycoords='data',
             xytext=(2, 4.5), fontsize=10,
             arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2"))
plt.annotate(r'A',
             xy=(4, 4), xycoords='data',
             xytext=(5, 4.5), fontsize=10,
             arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2"))

$\qquad$ 根据点到直线的距离公式，可以容易地算出支持向量机 $\mathbf{A}$ 到分隔超平面的距离为：
$d=\frac{|\mathbf{w}^T\mathbf{A}+b|}{||\mathbf{w}||}$
PS： $||w||$ 表示为2-范数。如，w是一个n维列向量，w=(w1,w2,…,wn)’;||w||=w’w。
PS：点到直线的距离公式： $d=\left|\frac{A x_{0}+B y_{0}+C}{\sqrt{A^{2}+B^{2}}}\right|$ ，公式中的直线方程为 $Ax+By+C=0$ ，点P的坐标为 $(x_0,y_0)$ 。

$\qquad$ 由于点 $\mathbf{A}$ 在直线 $\mathbf{w}^Tx+b=1$ 上，因此 $\mathbf{w}^T\mathbf{A}+b=1$ ，代入即可得，支持向量机 $\mathbf{A}$ 到分隔超平面的距离为 $d=\frac{1}{||\mathbf{w}||}$ 。为了使间距最大，我们只需要找到合适的参数 $\mathbf{w}$ 和 $b$ ，使 $\frac{1}{||\mathbf{w}||}$ 最大即可。 $\mathbf{w}$ 是向量 $\mathbf{w}$ 的 L2范数，其计算公式为：
$||w||=\sqrt{\sum_{i=1}^{n}w_i^2}$
由此可得，求 $\frac{1}{||\mathbf{w}||}$ 的最大值，等价于求 $||\mathbf{w}^2||$ 最小值：
$||w||^2=\sum_{j=1}^{n}w_j^2$
$\qquad$ 其中 $n$ 为向量 $\mathbf{w}$ 的维度。除了间距最大外，我们选出来的分隔超平面还要能正确地把数据集分类。问题来了，怎样在数学上表达出“正确地把数据集分类”这个描述呢？
$\qquad$ 回到图2中，可以容易地得出结论，针对方形的点 $x$ ，必定满足 $\mathbf{w}^T+b \geq 1$ 的约束条件。针对圆形的点 $x$ ，必定容易地得出结论，针对方形的点 $x$ ，必定满足 $\mathbf{w}^T+b \geq 1$ 的约束条件。针对圆形的点 $x$ ，必定满足 $\mathbf{w}^Tx+b \leq -1$ 的约束条件。类别是离散的值，我们使用-1来表示圆形的类别，用1来表示方形的类别，即 $y\in \{-1,1\}$ 。针对数据集中的所有样本 $\mathbf{x}^{(i)},\mathbf{y}^{(i)}$ ，只要它们都满足以下的约束条件，则由参数 $\mathbf{w}$ 和 $b$ 定义的分隔超平面即正确地把数据集分类：
$\mathbf{y}^{(i)}(\mathbf{w}^T\mathbf{x}^{(i)}+b)\geq 1$
$\qquad$ 等等，怎么得出这个数学表达式的呢？
$\qquad$ 其技巧在于使用 1 和 -1 来定义类别标签。针对 $\mathbf{y}^{(i)}=1$ 的情况，由于其满足 $\mathbf{w}^T\mathbf{x}^{(i)}+b\geq1$ 的约束，两遍都乘以 $\mathbf{y}^{(i)}$ 后，大于号保持不变。针对 $\mathbf{y}^{(i)}=-1$ 的情况，由于其满足 $\mathbf{w}^T\mathbf{x}^{(i)}+b \leq -1$ 的约束，两边都乘以 $y^{(i)}$ 后，负负得正，并且小于号变成了大于号。这样，我们就可以用一个公式来表达针对连个不同类别的约束函数了。
$\qquad$ 在逻辑回归算法里，使用 0 和 1 作为类别标签，而在这里我们使用 -1 和 1 作为类别标签。其目的都是为了让数学表达式尽量简洁。
$\qquad$ 一句话总结：求解 SVM 算法，就是在满足约束条件 $\mathbf{y}^{(i)}(\mathbf{w}^T\mathbf{x}^{(i)}+b)\geq1$ 的前提下，求解 $||w||^2$ 的最小值。

松弛系数

$\qquad$ 针对线性不可分的数据集，上面的方法就失灵了，因为无法找打最大间距的分隔超平面，如图 3 所示。
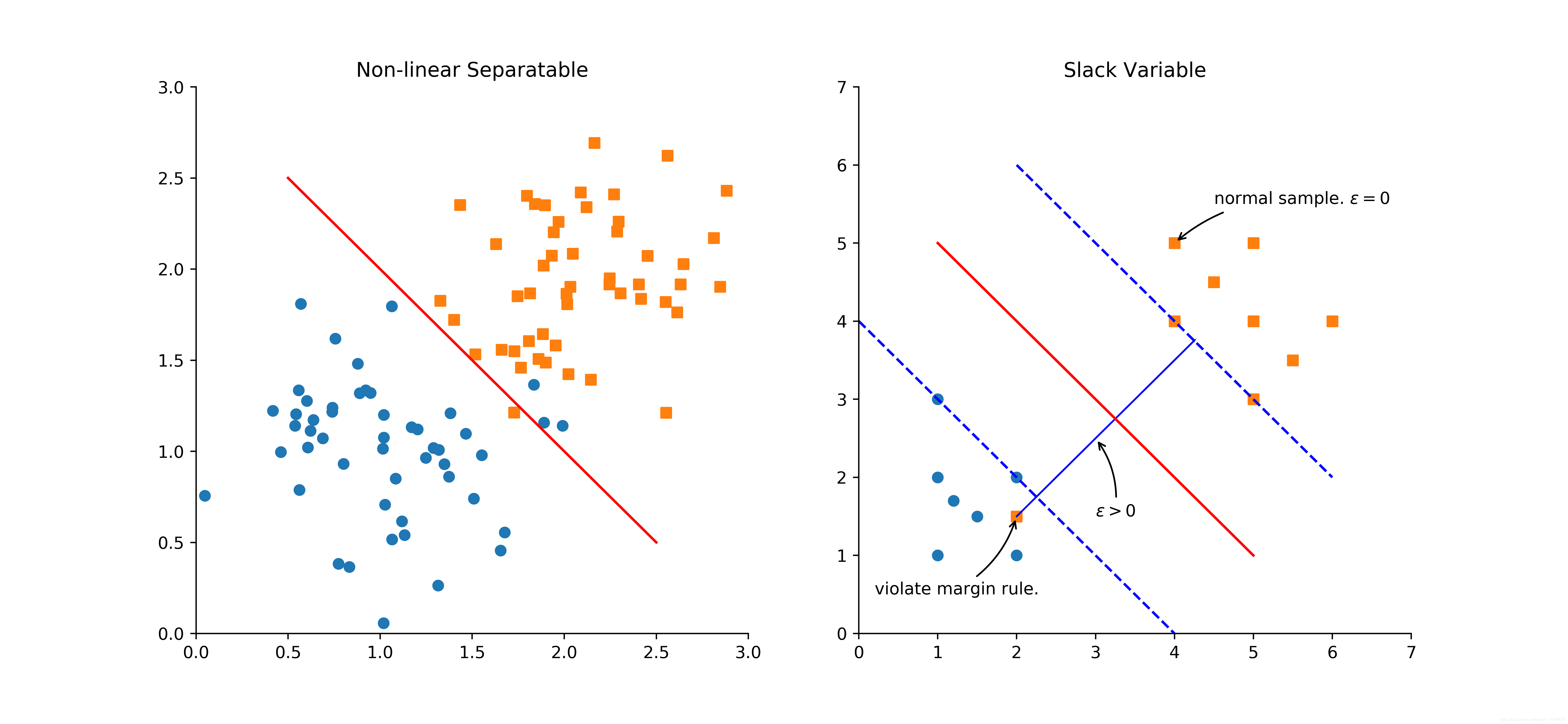
在这里插入图片描述
$\qquad$ 解决这个问题的方法是引入一个参数 $\varepsilon$ ，称为松弛系数。然后把优化的目标函数变为：
$\argmin||\mathbf{w}||^2+R\sum_{i=1}^{m}\varepsilon_i$
$\qquad$ 其中， $m$ 为数据集的个数， $R$ 为算法参数。其约束条件相应变为：
$\mathbf{y}^{(i)}(\mathbf{w}^T\mathbf{x}^{(i)}+b)\geq1-\varepsilon_i$
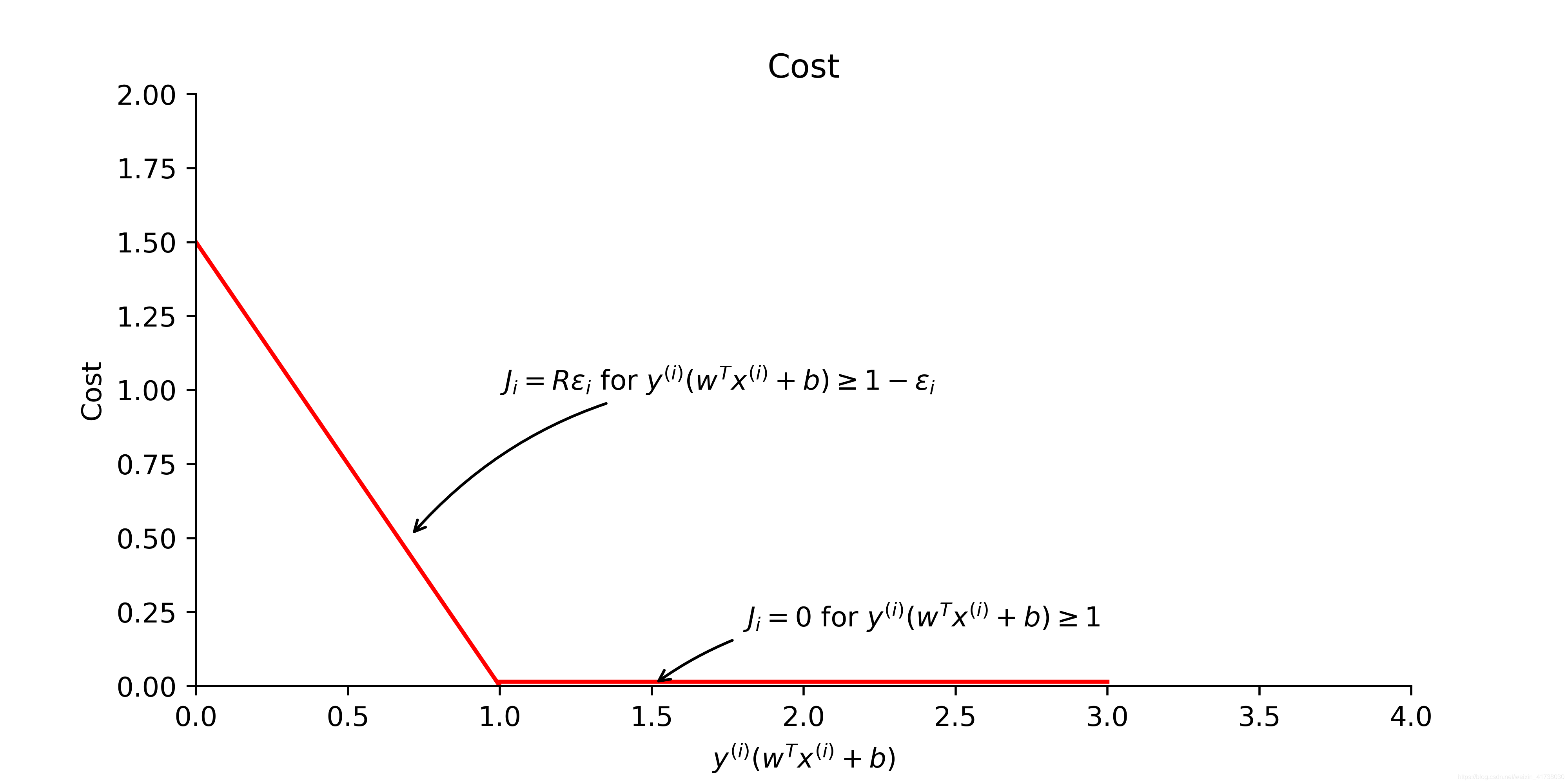
$\qquad$ 怎么理解松弛系数呢？我们可以把 $\varepsilon_i$ 理解为数据样本 $x^{(i)}$ 违反最大间距规则的程度，如图3所示，针对大部分“正常”的样本，即满足约束条件的样本 $\varepsilon=0$ 。而对部分违反最大间距规则的样本 $\varepsilon>0$ 。而参数 $R$ 则表示对违反最大间距规则的样本的“惩罚”力度。当 $R$ 选择一个很大的值时，我们的目标函数对违反最大间距规则的点的“惩罚力度”将变得很大。当 $R$ 选择一个比较小的值时，针对那些违反最大间距规则的样本，其“付出的代价”不是特别大，我们的模型就会倾向于部分点违反最大的间距规。我们可以把 $\mathbf{y}^{(i)}(\mathbf{w}^Tx^{(i)}+b)$ 作为横坐标，把样本由于违反约束条件所付出的代价 $J_i$ 作为纵坐标，可以画出如图 4 所示的关系图。
$\qquad$ 从如图4可以清楚地看出来，针对那些没有违反约束条件 $\mathbf{y}^{(i)}(\mathbf{w}^Tx^{(i)}+b) \geq 1$ 的样本，其成本为0。而针对那些违反了约束条件的样本 $\mathbf{y}^{(i)}(\mathbf{w}^Tx^{(i)}+b) \geq 1-\varepsilon_i$ ，其成本与 $\varepsilon$ 成正比，如图4中所示，斜线的斜率为 $R$ 。
$\qquad$ 从这里的描述可知，引入松弛系数类似于逻辑回归算法里的成本函数引入正则项，目的都是为了纠正过拟合问题，让支持向量机对噪声数据有更强的适应性。如图3的右图所示，当出现一些违反间距规则的噪声样本时，仍然希望我们的分割超平面是原来的样子，这就是松弛系数的作用。
在这里插入图片描述

核函数

$\qquad$ 什么是核函数？核函数是特征转换函数。这是非常抽象的描述，本节的内容就是炜乐理解这个抽象的概念。

最简单的核函数

$\qquad$ 回顾上一节介绍的内容，我们的任务是找出合适的参数 $w,b$ ，使得由它们决定的分隔超平面、间距最大，且能正确地对数据集进行分类。间距最大是我们的优化目标，正确地对数据集进行分类是约束条件。用数学来表达，在满足约束条件 $\mathbf{y}^{(i)}(\mathbf{w}^Tx^{(i)}+b) \geq 1$ ，即 $\mathbf{y}^{(i)}(\mathbf{w}^Tx^{(i)}+b) -1\geq 0$ 的前提下，求 $\frac{1}{2}||w||^2$ 的最小值。
$\qquad$ 拉格朗日乘子法 是解决约束条件下，求函数极值的理想方法。其方法是引入非负系数 $\alpha$ 来作为约束条件的权重：
$L=\frac{1}{2}||\mathbf{w}||^2-\sum_{i=1}^m\alpha_i{(\mathbf{y}^{(i)}z(\mathbf{w}^T\mathbf{x}^{(i)}+b)-1)}$
$\qquad$ 公式中，针对数据集中的每个样本 $x^{(i)},y^{(i)}$ ，都有一个系数 $\alpha_i$ 与之对应。学习过微积分的读者都指导，及指出的偏导数为0.我们先求 $L$ 对 $\mathbf{w}$ 的偏导数：
$\frac{\partial L}{\partial b} = w- \sum_{i=1}^{m}\alpha_iy^{(i)}x^{(i)}=0$
$\qquad$ 从而得到 $\mathbf{w}$ 和 $\alpha$ 的关系：
$\mathbf{w}=\sum_{i=1}^m\alpha_i\mathbf{y}^{(i)}\mathbf{x}^{(i)}$
$\qquad$ 至此，读者应该知道，我们为什么要把求 $\frac{2}{||\mathbf{w}||}$ 的最大值转换为求 $\frac{1}{2}||w||^2的最小值$ 。其目的是炜乐使得 $\mathbf{w}$ 的数学表达尽量简洁优美。接着我们继续先求 $L$ 对 $b$ 的偏导数：
$\frac{\partial{L}}{\partial{b}}=\sum_{i=1}^m\mathbf{y}^{(i)}\alpha_i=0$
$\qquad$ 把 $\mathbf{w}=\sum_{i=1}^m\alpha_i\mathbf{y}^{(i)}\mathbf{x}^{(i)}$ 和 $\sum_{i=1}^my^{(i)}\alpha_i=0$ 代入 $L$ ，通过代数运算可得：
$L=\sum_{i=1}^{m}\alpha_i-\frac{1}{2}\sum_{i=1}^m\sum_{j=1}^m\alpha_i\alpha_j\mathbf{y}^{(i)}\mathbf{y}^{(j)}\mathbf{x}^{(i)T}\mathbf{x}^{(j)}$
$\qquad$ 这个公式看起来很复杂。我们解释一下公式里各个变量的含义。其中， $m$ 是数据集的个数， $\alpha$ 是拉格朗日乘子法引入的一个系数，针对数据集中的每个样本 $x^{(i)}$ ，都有对应的 $\alpha_i$ 。 $\mathbf{x}^{(i)}$ 是数据集中第 $i$ 个样本的输入，它是一个向量， $\mathbf{y}^{(i)}$ 是数据集第 $i$ 个样本的输出标签，其值为 $\mathbf{y}^{i}\in\{-1,1\}$ 。
$\qquad$ 怎么求这个公式的最小值，是数值分析（numerical analysis）这个数学分支要解决的问题，这是一个典型的二次规划问题。目前广泛应用的是一个成为 SMO（序列最小优化）的算法。这些内容不再进一步展开，感兴趣的读者可以查阅相关资料。
$\qquad$ 最后求解出来的 $\alpha$ 有个明显的特点，即大部分 $\alpha_i=0$ ，这个结论背后的原因很直观，因为只有那些支持向量所对应的样本，直接决定了间隙的大小，其他离分隔超平面太远的样本，对间隙大小根本没有影响。读者可以参考本章开头的图 8-1 加深一下印象。
$\qquad$ 读到这里，相信读者心里会有疑问：你用拉格朗日乘子法加上一大堆偏导数运算，最后推导出来的公式复杂到无法展开进一步论述其求解方法，那些做这些事情和公式推导的意义在哪里呢？实际上，推导出这个公式的主要目的是为了引入支持向量机的另一个核心概念：核函数。
$\qquad$ 我们注意到 $L$ 里的 $\mathbf{x}^{(i)T}\mathbf{x}^{(j)}$ 部分，其中 $x^{(i)}$ 是一个特征向量，所以 $\mathbf{x}^{(i)T}\mathbf{x}^{(j)}$ 是一个数值，它是两个输入特征向量的内积。另外，我们的预测函数为：
$\hat{y}=\mathbf{w}^T\mathbf{x}=\sum_{i=1}^m\alpha_iy^{(i)}\mathbf{x}^{(i)T}\mathbf{x}+b$
$\qquad$ 当 $\hat{y} > 0$ 时，我们预测为类别 1，当 $\hat{y} < 0$ 时，我们预测为类别-1。注意到预测函数里也包含式子 $\mathbf{x}^{(i)T}\mathbf{x}$ 。我们把 $K(\mathbf{x}^{(i)},\mathbf{x}^{(j)})=0$ 。引入核函数后，我们的预测函数就变成：
$\hat{y}=\sum_{i=1}^{m}\alpha_iy^{(i)}K(x^{(i)},x)+b$

相似性函数

$\qquad$ 请读者朋友思考一下，为什么我们需要引入核函数？假设我们有一个数据集，只有一个输入特征，要对这个数据集进行分类。由于只有一个输入特征，这些训练样本分布在一条直线上，此时我们很难找出一个分隔超平面来分隔这个数据集，如图5左图所示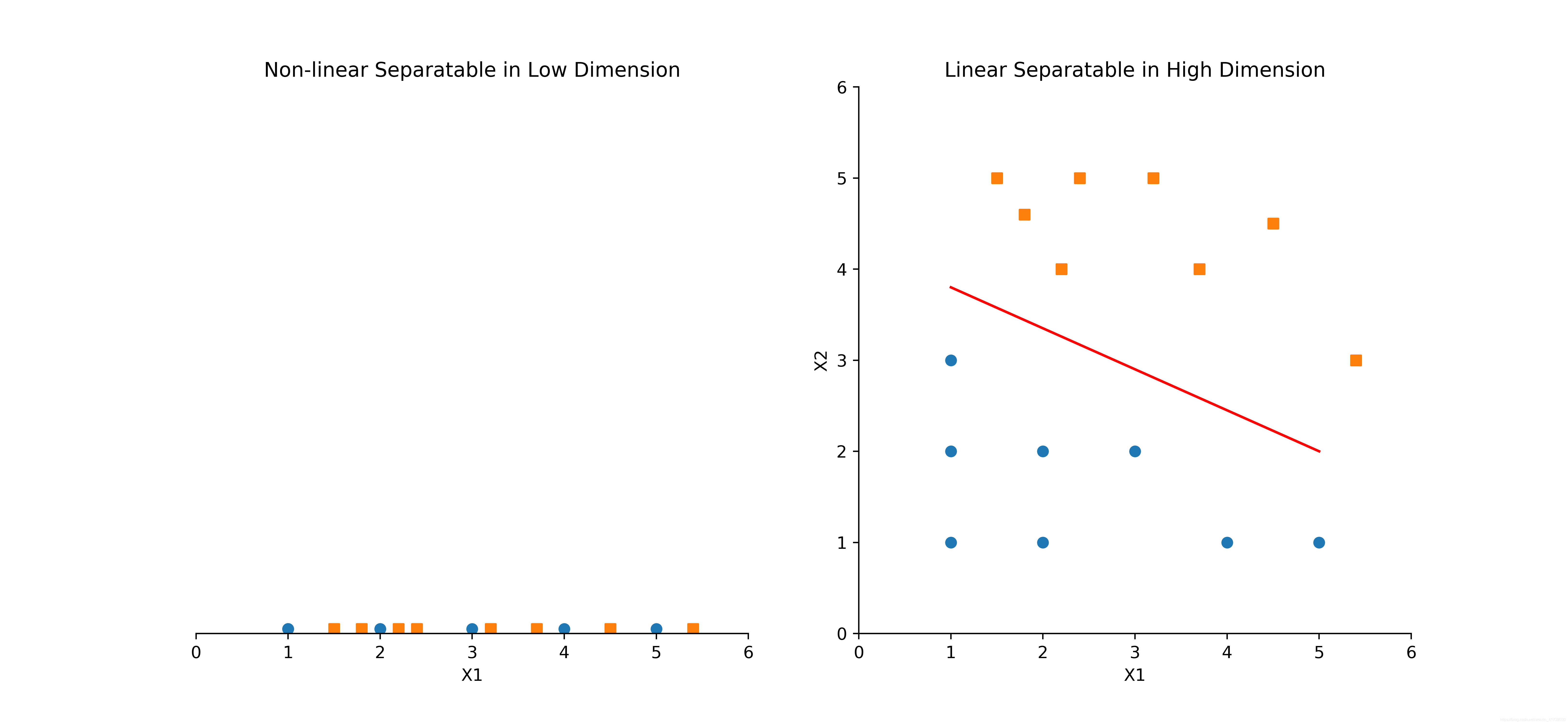：在这里插入图片描述
$\qquad$ 为了解决这个问题，我们可以想办法，用一定的规则把这些无法进行线性分隔的样本，映射到更高纬度的空间里，然后在高纬度空间里找出分隔超平面。针对这个例子，把一维空间上的样本映射到二维空间，这样很容易就找出一个分隔平面把这些样本分离开，如图5右图所示。
$\qquad$ SVM的和函数就是为了实现这种相似性映射。从上一节我们可以知道，最简单的和函数是 $K(\mathbf{x}^{(i)}\mathbf{x}^{(j)})=\mathbf{x}^{(i)T}\mathbf{x}^{(j)}$ ，它衡量的是两个输入特征向量的相似性。可以通过定义核函数 $K(\mathbf{x}^{(i)},\mathbf{x}^{(j)})$ 来重新定义相似性，从而得到想要的映射。例如在基因测序领域，我们需要根据 DNA 分子的特征来定义相似性函数，即核函数。在文本处理领域，也可以自己定义和函数来衡量两个词之间的相似性。
$\qquad$ 怎样把低维度的空间映射到高纬度的空间呢？大家是否还记得我们介绍过的一个解决欠拟合的方法，就是使用多项式来增加特征数，这个本质上就是从低维度映射到高纬度。针对图5中的例子，我们的输入特征是一维的，即只有 $[\mathbf{x}_1]$ 变量，如果我们要变成二维的，一个方法是把输入特征变为 $[x_1,2x_1^2]$ ，此时的输入特征就变成了一个二维的向量。定义这种特征映射的函数为 $\phi(x)$ ，称之为相似性函数。针对输入特征向量 $\mathbf{x}$ ，经过 $\phi(x)$ 作用后，会变成一个新的、更高维度的输入特征向量。这样在原来低纬度计算相似性的运算 $\mathbf{x}^{(i)T}\mathbf{x}^{(j)}$ ，就可以转换为高纬度空间里进行相似性运算 $\phi{(\mathbf{x}^{(i)})^T\phi(\mathbf{x}^{(j)})}$ 。
$\qquad$ 思考：核函数 $K(x^{(i)})$ 和相似性函数 $\phi(x)$ 有什么关系？
$\qquad$ 相似性函数是特征映射函数，比如针对二维的特征向量 $[x_1,x_2]$ ，我们可以定义相似性函数 $\phi(x)=[x_1,x_2,x_1x_2,x_1^2,x_2^2]$ 。经过相似性函数转换后，二维的特征向量就变成了五维的特征向量。而核函数定义为特征向量的内积，经过相似性函数 $\phi(x)$ 转换后，核函数即变为两个五维特征向量的内积，即 $K(x^{(i)},x^{(j)})=\phi(x^{(i)})^T\phi(x^{(j)})$ 。
$\qquad$ 这里我们介绍相似性函数 $\phi(x)$ 的目的，是为了帮助大家理解核函数的生成过程有其背后的思想。在实际计算的过程中，我们不会计算相似性函数及其映射值，因为这样做的计算效率很低。例如，我们把二维的空间映射到 $n$ 维的空间，如果 $n$ 非常大，要在 $n$ 维的空间里计算两个向量的内积，需要 $n^2$ 次运算才可以完成，这个计算成本是非常高的。

常用的核函数

$\qquad$ 核函数一般和应用场景相关，例如我们说的基因测序领域和在文本处理领域，它们的核函数可能是不一样的，有专门针对特定应用领域进行核函数开发和建模的科研人员在从事这方面的研究。虽然核函数和应用场景相关，但实际上还是有一些通用的、“万金油”式的核函数。常用的核函数有两种，一种是多项式核函数，顾名思义，是对输入特征向量增加多项式的一种相似性映射函，其数学表达式为：
$K(x^{(i)},x^{(j)})=(\gamma x^{(i)T}x^{(j)}+c)^n$
$\qquad$ 其中 $\gamma$ 为正数， $c$ 为非负数。我们介绍过线性核函数 $K(x^{(i)},x^{(j)})=x^{(i)T}x^{(j)}$ 是多项式和函数在 $n=1,\gamma=1,c=0$ 处的一种特例。在二维空间里， $K(x^{(i)}，x^{(j)})=x^{(i)T},x^{(j)}$ 只能表达直线的分隔超平面，而多项式函数 $K(x^{(i)},x^{(j)})=(\gamma x^{(i)T}x^{(j)}+c)^n$ 在 $n>1$ 时，可以表达更复杂的、非直线的分隔超平面。
$\qquad$ 另外一种常用的核函数是高斯核函数，其数学表达式为:
$K(x^{(i)},x^{(j)}=\exp(-\frac{(x^{(i)}-x^{(j)})^2}{2\sigma^2})$
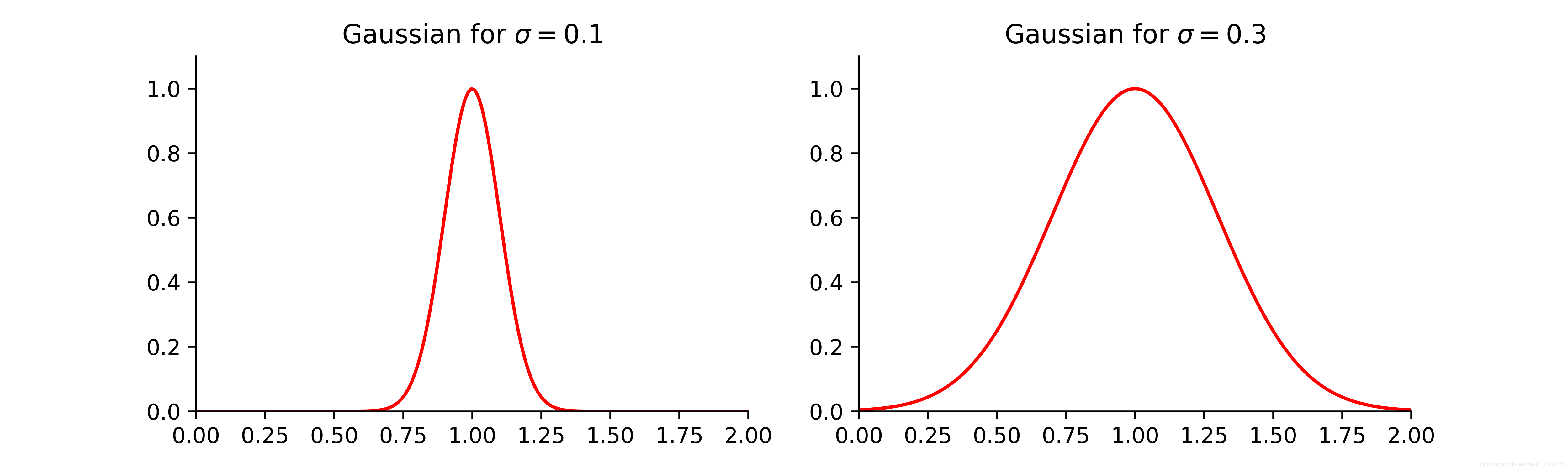
$\qquad$ 如果我们的输入特征是一维的标量，那么高斯核函数对应的形状就是一个反钟形的曲线，其参数 $\sigma$ 控制反钟性的宽度，如图6：
在这里插入图片描述
$\qquad$ 由于 $K(x^{(i)},x^{(j)})=x^{(i)T}x^{(j)}$ ，经过合适的数学变换，可得高斯核函数对应的特征转换函数为：
$\phi(x)=\sum_{i=0}^{\infty}\exp(-x^2)\sqrt{\frac{2^i}{i!}}x^i$
$\qquad$ 注意前面无限多项的累加器 $\sum_{i=0}^{\infty}$ ，其物理意义就是把特征向量转换到无限多维向量空间里，即高斯核函数可以把输入特征向量扩展到无限维空间里。公式的推导过程会用到泰勒展开式，感兴趣的读者可以在 YouTube 上搜索 Gaussian Kernel Hsuan-Tien Lin，这是林轩田的一个机器学习视频。
$\qquad$ 接下来看一下高斯核函数对应的预测函数：
$\hat{y}=\sum_{i=1}^m\alpha_iy^{(i)}K(x^{(i)},x)+b$
$\qquad$ 其中 $K(x^{(i)},x)$ 是高斯核函数，而 $\alpha_i$ 只在支持向量对应的样本处不为0，其他的样本为0。由此得知，预测函数是中心点在支持向量处的高斯函数的线性组合，其线性组合的系数为 $\alpha_iy^{(i)}$ 。由此，高斯核函数也成为 RBF(Radial Basis Function)核函数，即反钟形函数的线性组合。

核函数的对比

$\qquad$ 本节将对我们学习的几个核函数进行对比，看看它们各有那些优缺点。
$\qquad$ 1. 线性函数
$K(x^{(i)},x^{(j)})=x^{(i)T}x^{(j)}$
$\qquad$ 这是我们接触到的最简单的核函数，它直接计算两个输入特征向量的内积。它的有点是简单、运算效率高，因为不涉及复杂的变换；结果容易解释，因为总是能生成一个最简单的线性分隔超平面。它的缺点也很明显，即对线性不可分的数据集没有很好的办法。
$\qquad$ 2. 多项式核函数
$K(x^{(i)},x^{(j)})=(\gamma x^{(i)T}x^{(j)}+c)^n$
$\qquad$ 多项式核函数通过多项式来作为特征映射函数，它的优点是可以拟合出复杂的分隔超平面。它的缺点是可选的参数太多，有 $\gamma,c,n$ 这 3 个参数要选择，在实践过程中，选择一组合适的参数会变得比较困难；另外一个缺点是，多项式的阶数 $n$ 不宜太高，否则会给模型求解带来一些计算的苦难。典型地，当 $x^{(i)T}x^{(j)}<1$ 时，经过 $n$ 次方运算后，会接近于0，而当 $x^{(i)T}x^{(j)}>1$ 时，经过 $n$ 次方运算后，会接近于0，而当 $x^{(i)T}x^{(j)} > 1$ 时，经过 $n$ 次方运算后，又会变得非常大，这样和函数就会变的不够稳定。
$\qquad$ 3. 高斯核函数
$K(x^{(i)},x^{(j)})=\exp(-\frac{(x^{(i)}-x^{(j)})^2}{2\sigma^2})$
$\qquad$ 高斯核函数可以把输入特征映射到无限多维，所以它会比线性核函数功能上要强大很多，并且没有多项式函数的数值计算那么困难，因为它的核函数计算出来的值永远在 $[0,1]$ 之间。高斯核函数还有一个优点是参数容易选择，因为它只有一个参数 $\sigma$ 。它的缺点是不容易解释，因为映射到无限多维向量空间这个事情显得太不直观；计算速度比较慢；容易造成过拟合，原因是映射到无限维向量空间，这是个非常复杂的模型，它会试图去拟合所有样本，从而造成过拟合。
$\qquad$ 在实践中怎么选择核函数呢？更进一步，逻辑回归算法也可以用来解决分类问题，到底是用逻辑回归算法还是用 SVM 算法呢？假设 $n$ 是特征个数； $m$ 是训练数据集的样本个数，一般可以按照下面的规则来选择算法。
$\qquad$ 如果 $n$ 相对 $m$ 来说比较大，例如 $n=10,000,m=10\sim1000$ ，如文本处理问题，这个时候使用逻辑回归或线性函数的 SVM 算法都可以；如果 $n$ 比较小， $m$ 中等大小。例如 $n=1\sim1000,m=10\sim~10,000$ ，那么可以使用高斯核函数的 SVM 算法；如果 $n$ 比较小， $m$ 比较大，例如 $n=1\sim1000,m=50,000+$ ，那么一般需要增加特征，此时需要使用多项式函数或高斯核函数的 SVM 算法。
$\qquad$ 更一般性的算法选择原则是，针对数据量很大的问题，我们可以选择复杂一点的模型。虽然复杂模型容易造成过拟合，但由于数据量很大，可以有效地弥补过拟合的问题。如果数据量比较小，一般需要选择简单一点的模型，否则很容易造成过拟合，此时要特别注意模型是否欠拟合，如果出现了欠拟合，可以使用增加多项式特征的方法纠正欠拟合的问题。读到这里，读者的脑海里要想象出一幅过拟合和欠拟合时的学习曲线图。

scikit-learn里的SVM

$\qquad$ scikit-learn 里对 SVM 的算法实现都在包 sklearn.svm 下面，其中 SVC 类使用来进行分类的任务，SVR 是用来进行数值回归任务的。读者可能会有疑问，SVM 是不是用来进行分类的算法吗，为什么可以用来进行数值回归？实际上，这是是数学上的一些扩展而已，在计算机里，可以用离散的数值计算来代替连续的数值回归。
$\qquad$ 我们以 SVC 为例，首先需要选择 SVM 的核函数，由参数 kernel 指定，其中 linear 表示本章介绍的线性函数，它只能产生直线形状的分隔超平面；poly表示本章介绍的多项式核函数，用它可以构建出复杂形状的分隔超平面; rbf 表示高斯核函数。
$\qquad$ 不同的核函数需要指定不同的参数。针对线性函数，只需要指定参数 C，它表示对不符合最大间距规则的样本的惩罚力度，即在前面有所介绍的系数 R，针对多项式核函数，除了参数 C外，还需要指定 degree，它表示多项式的阶数。针对高斯核函数，除了参数 C 外，还需要指定 gamma 值，这个值对应前面中介绍的高斯核函数公式里的 $\frac{1}{2\sigma^2}$ 的值。
$\qquad$ 下面先来看一个简单的例子。我们生成一个有两个特征、包含两种类别的数据集，然后用线性核函数的 SVM算法进行分类：

import matplotlib.pyplot as plt
import numpy as np


def plot_hyperplane(clf, X, y, 
                    h=0.02, 
                    draw_sv=True, 
                    title='hyperplan'):
    # create a mesh to plot in
    x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
    y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
                         np.arange(y_min, y_max, h))

    plt.title(title)
    plt.xlim(xx.min(), xx.max())
    plt.ylim(yy.min(), yy.max())
    plt.xticks(())
    plt.yticks(())
    
    Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
    # Put the result into a color plot
    Z = Z.reshape(xx.shape)
    plt.contourf(xx, yy, Z, cmap='hot', alpha=0.5)

    markers = ['o', 's', '^']
    colors = ['b', 'r', 'c']
    labels = np.unique(y)
    for label in labels:
        plt.scatter(X[y==label][:, 0], 
                    X[y==label][:, 1], 
                    c=colors[label], 
                    marker=markers[label])
    if draw_sv:
        sv = clf.support_vectors_
        plt.scatter(sv[:, 0], sv[:, 1], c='y', marker='x')


from sklearn import svm
from sklearn.datasets import make_blobs

X, y = make_blobs(n_samples=100, centers=2, 
                  random_state=0, cluster_std=0.3)
clf = svm.SVC(C=1.0, kernel='linear')
clf.fit(X, y)

plt.figure(figsize=(12, 4), dpi=144)
plot_hyperplane(clf, X, y, h=0.01, 
                title='Maximum Margin Hyperplan')

$\qquad$ 输出的图形如下图所示，其中带有 X 标记的点即为支持向量，它保存在模型的 support_vectors里。
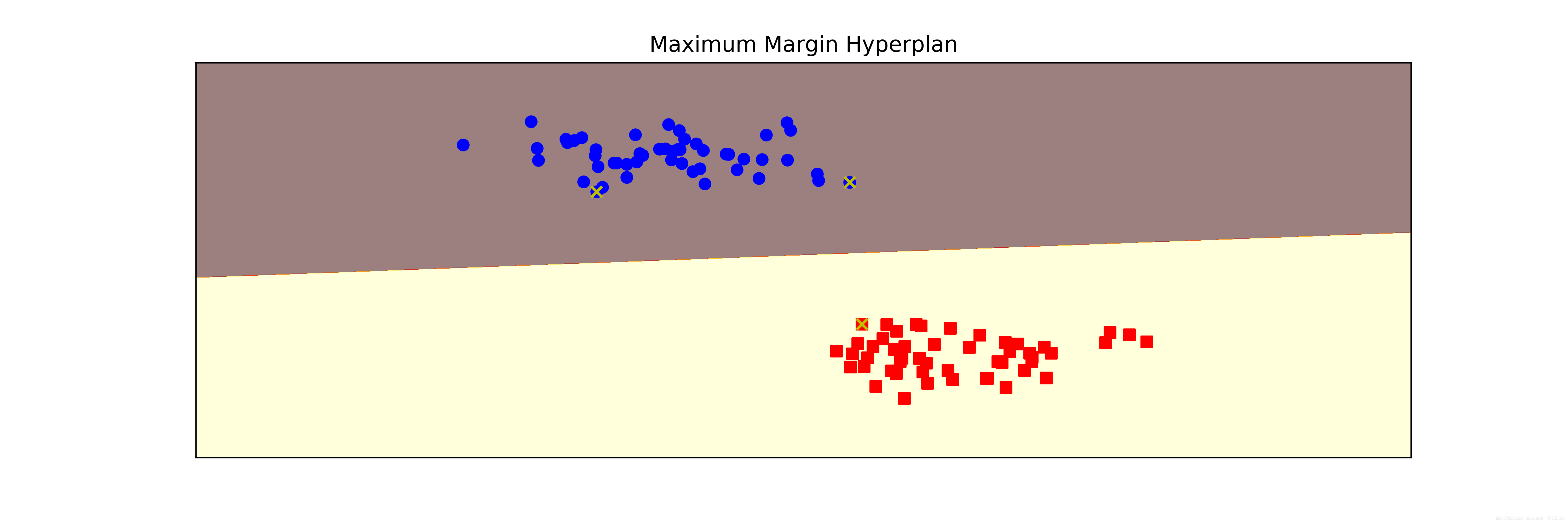
在这里插入图片描述
$\qquad$ 此时需要注意的是 plot_hyperplane() 函数，其主要功能是画出样本点，同时画出分类区间。它的主要原理是使用numpy.meshgrid()生成一个坐标矩阵，然后预测坐标矩阵中每个点所属的类别，最后用 coutourf() 函数，为坐标矩阵中不同类别的点填充不同的颜色。其中，contourf() 是画等高线并填充颜色的函数。
$\qquad$ 接着来看另外一个例子，我们生成一个有两个特征、包含三种类别的数据集，然后分别构造成4个 SVM 算法来拟合数据集，分别是线性核函数、三阶多项式核函数、 $\gamma=0.5$ 的高斯核函数，以及 $\gamma=0.1$ 的高斯核函数。最后把这 4 个 SVM 算法拟合出来的分隔超平面出来。

from sklearn import svm
from sklearn.datasets import make_blobs

X, y = make_blobs(n_samples=100, centers=3, 
                  random_state=0, cluster_std=0.8)
clf_linear = svm.SVC(C=1.0, kernel='linear')
clf_poly = svm.SVC(C=1.0, kernel='poly', degree=3)
clf_rbf = svm.SVC(C=1.0, kernel='rbf', gamma=0.5)
clf_rbf2 = svm.SVC(C=1.0, kernel='rbf', gamma=0.1)

plt.figure(figsize=(10, 10), dpi=144)

clfs = [clf_linear, clf_poly, clf_rbf, clf_rbf2]
titles = ['Linear Kernel', 
          'Polynomial Kernel with Degree=3', 
          'Gaussian Kernel with $\gamma=0.5$', 
          'Gaussian Kernel with $\gamma=0.1$']
for clf, i in zip(clfs, range(len(clfs))):
    clf.fit(X, y)
    plt.subplot(2, 2, i+1)
    plot_hyperplane(clf, X, y, title=titles[i])

$\qquad$ 输出的图形如下图所示，其中带有 x 标志的点即为支持向量。
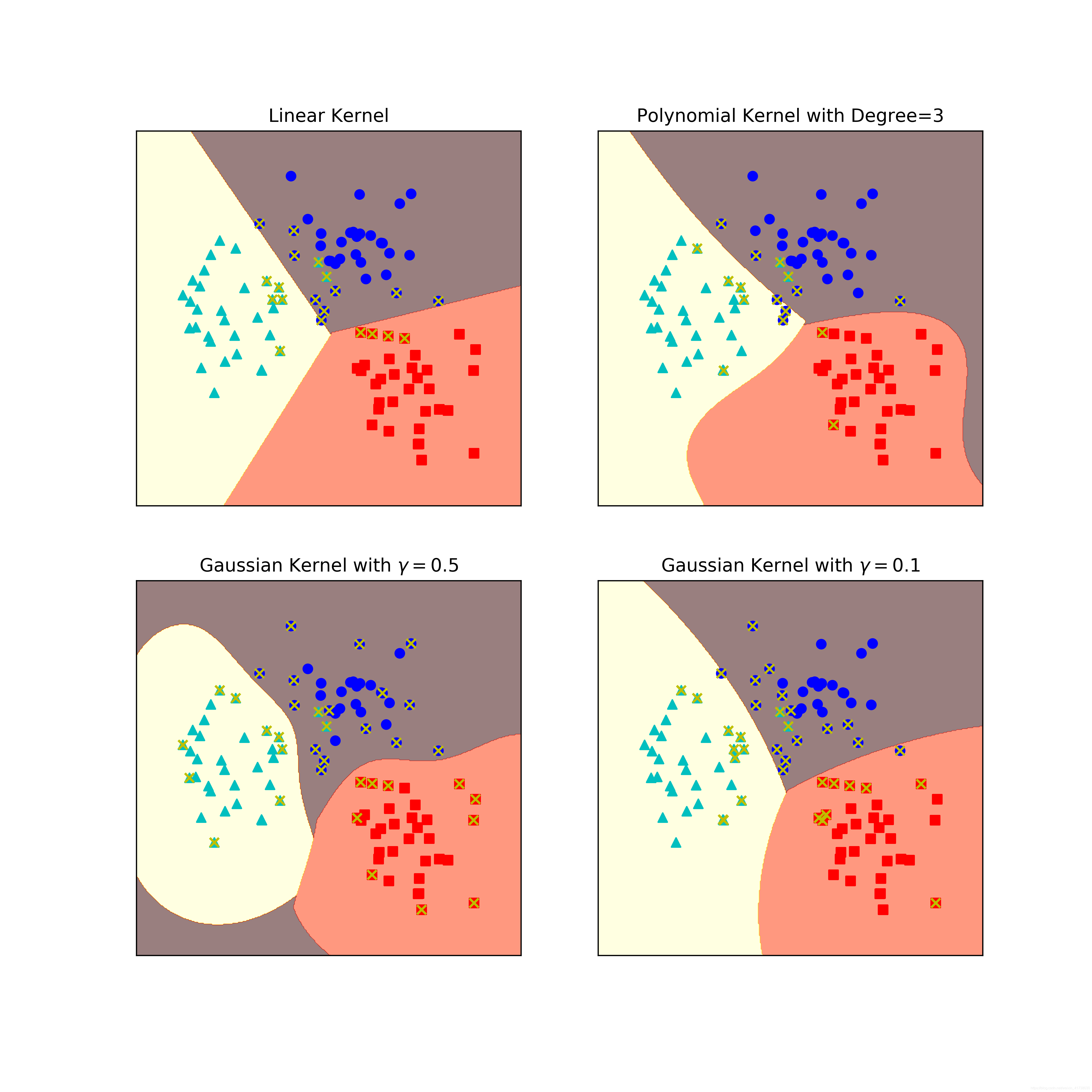
在这里插入图片描述
$\qquad$ 如上图的左上角是线性核函数，它只能拟合出直线分隔超平面。右上角是三阶多项式核函数，它能拟合出复杂曲线分隔超平面。左下角是 $\gamma=0.5$ 的高斯核函数，右下角是 $\gamma=0.1$ 的高斯核函数，通过调整参数 $\gamma$ 的值，可以调整分隔超平面的形状。典型地， $\gamma$ 值太大，越容易造成过拟合， $\gamma$ 值太小，高斯核函数会退化成线性核函数。
$\qquad$ 思考：请读者留意上图左下角 $\gamma=0.5$ 的高斯核函数的图片，带有 x 标记的点是支持向量。我们之前介绍过，离分隔超平面最近的点是支持向量，为什么很多离分隔超平面很远的点，也是支持向量呢？
$\qquad$ 原因是高斯核函数把输入特征向量映射到了无限维的向量空间里，在映射后的高维向量空间里，这些点其实是离分隔超平面最近的点。当回到二维向量空间中时，这些点“看起来”就不像是距离分隔超平面最近的点了，但实际上他们就是支持向量。

实例：乳腺癌检测

$\qquad$ 我们以前使用逻辑回归算法进行了乳腺癌检测模型的学习和训练。本章使用支持向量机来解决这个问题。首先，我们载入数据：

import matplotlib.pyplot as plt
import numpy as np
# 载入数据
from sklearn.datasets import load_breast_cancer

cancer = load_breast_cancer()
X = cancer.data
y = cancer.target
print('data shape: {0}; no. positive: {1}; no. negative: {2}'.format(
    X.shape, y[y==1].shape[0], y[y==0].shape[0]))
    
from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)

$\qquad$ 输出如下：

data shape: (569, 30); no. positive: 357; no. negative: 212

$\qquad$ 可以看出，我们的数据集很小。高斯核函数太复杂，容易造成过拟合，模型效果应该不会很好。我们先占用高斯核函数试一下看与我们猜测的是否一致：

from sklearn.svm import SVC

clf = SVC(C=1.0, kernel='rbf', gamma=0.1)
clf.fit(X_train, y_train)
train_score = clf.score(X_train, y_train)
test_score = clf.score(X_test, y_test)
print('train score: {0}; test score: {1}'.format(train_score, test_score))

$\qquad$ 输出结果如下：

train score: 1.0; test score: 0.6491228070175439

$\qquad$ 训练数据集分数越接近满分，而交叉验证数据集的评分很低，这是典型的过拟合现象。代码中选择了 gamma 参数为0.1，这个值相对已经比较小了。
$\qquad$ 当然，我们完全可以自动来选择参数。可以用 GridSearchCV 来自动选择参数。我们看看如果使用高斯模型，最优的 gamma 参数值是多少，其对应的模型交叉验证评分是多少。

from common.utils import plot_param_curve
from sklearn.model_selection import GridSearchCV

gammas = np.linspace(0, 0.0003, 30)
param_grid = {'gamma': gammas}
clf = GridSearchCV(SVC(), param_grid, cv=5)
clf.fit(X, y)
print("best param: {0}\nbest score: {1}".format(clf.best_params_,
                                                clf.best_score_))

plt.figure(figsize=(10, 4), dpi=144)
plot_param_curve(plt, gammas, clf.cv_results_, xlabel='gamma');

$\qquad$ 在笔者计算机上的输出结果如下：

best param: {'gamma': 0.00011379310344827585}
best score: 0.9367311072056239

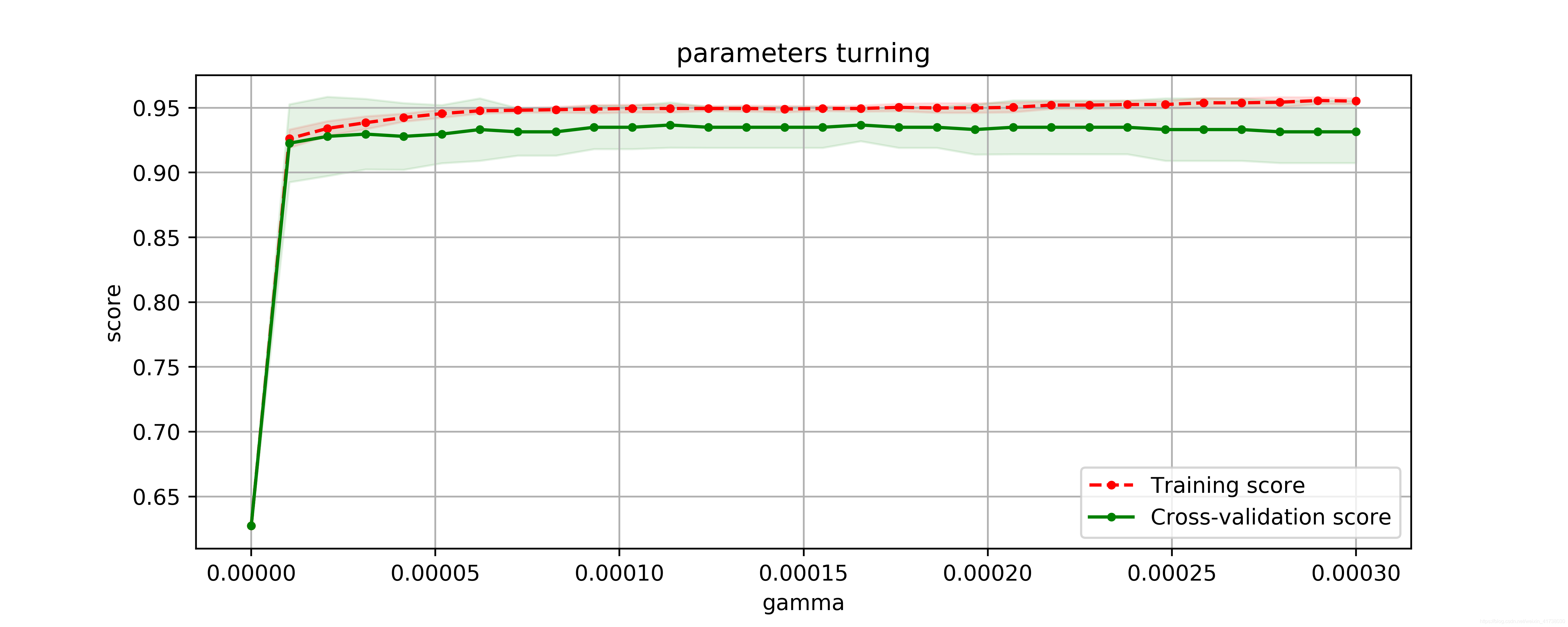
在这里插入图片描述
$\qquad$ 由此可见，即使是最好的 gamma 参数下，其平均最优得分也只是 0.9367311072056239。我们选择在 gamma 为 0.01 时，画出学习曲线，更直观地观察模型拟合情况。

import time
from common.utils import plot_learning_curve
from sklearn.model_selection import ShuffleSplit

cv = ShuffleSplit(n_splits=10, test_size=0.2, random_state=0)
title = 'Learning Curves for Gaussian Kernel'

start = time.clock()
plt.figure(figsize=(10, 4), dpi=144)
plot_learning_curve(plt, SVC(C=1.0, kernel='rbf', gamma=0.01),
                    title, X, y, ylim=(0.5, 1.01), cv=cv)

print('elaspe: {0:.6f}'.format(time.clock()-start))

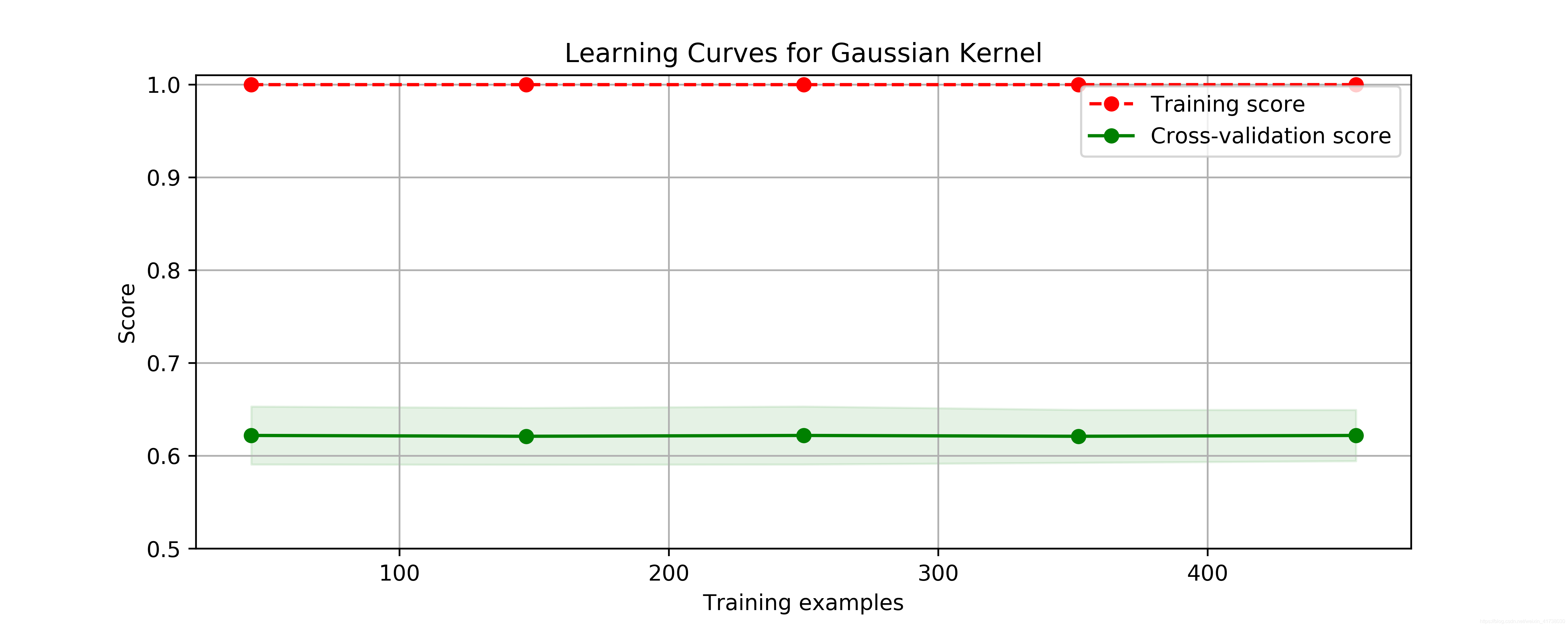
在这里插入图片描述
$\qquad$ 这是明显的过拟合现象，交叉验证数据集的评分比较低，且离训练数据集评分非常远。接下来换一个模型，使用二阶多项式核函数来拟合模型，看看结果如何。

from sklearn.svm import SVC

clf = SVC(C=1.0, kernel='poly', degree=2)
clf.fit(X_train, y_train)
train_score = clf.score(X_train, y_train)
test_score = clf.score(X_test, y_test)
print('train score: {0}; test score: {1}'.format(train_score, test_score))

$\qquad$ 笔者计算机上的输出结果如下：

train score: 0.9692307692307692; test score: 0.9736842105263158

$\qquad$ 看起来结果好多了。作为对比，我们画出一阶多项式和二阶多项式的学习曲线，观察模型的拟合情况。

import time
from common.utils import plot_learning_curve
from sklearn.model_selection import ShuffleSplit

cv = ShuffleSplit(n_splits=5, test_size=0.2, random_state=0)
title = 'Learning Curves with degree={0}'
degrees = [1, 2]

start = time.clock()
plt.figure(figsize=(12, 4), dpi=144)
for i in range(len(degrees)):
    plt.subplot(1, len(degrees), i + 1)
    plot_learning_curve(plt, SVC(C=1.0, kernel='poly', degree=degrees[i]),
                        title.format(degrees[i]), X, y, ylim=(0.8, 1.01), cv=cv, n_jobs=4)

print('elaspe: {0:.6f}'.format(time.clock()-start))

$\qquad$ 其输出的图形如下图所示：
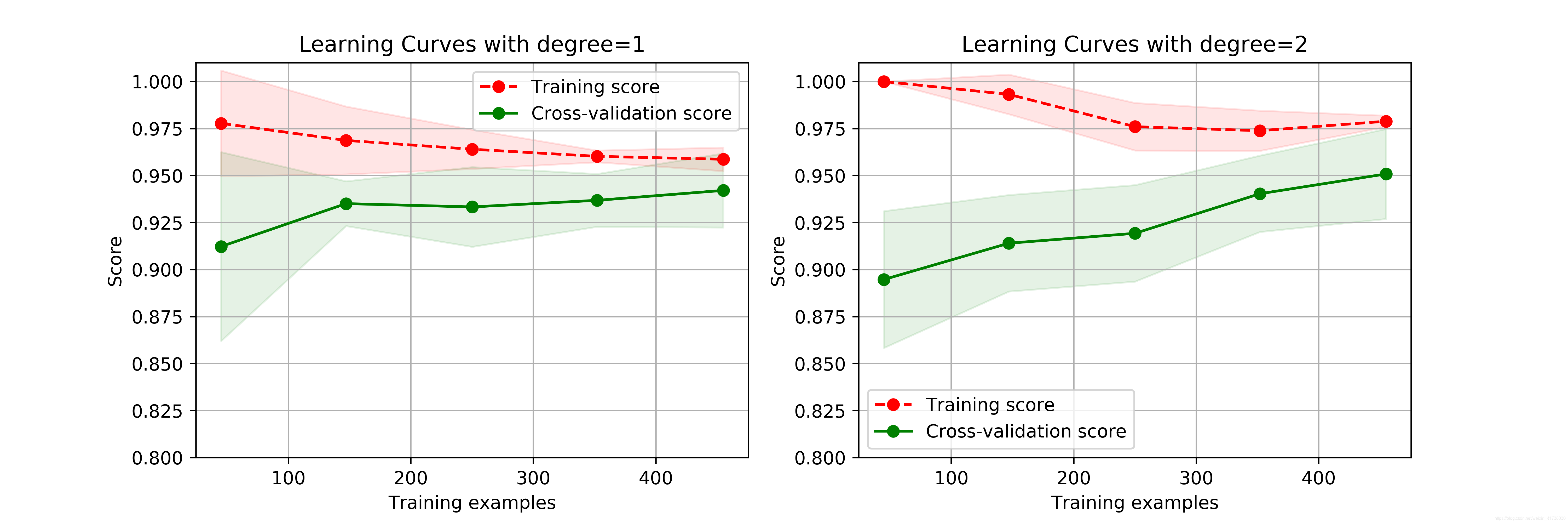
在这里插入图片描述
$\qquad$ 从图中可以看出，二阶多项式核函数的拟合效果更好。平均交叉验证数据集评分可达0.95，最高时达到0.975。运行段示例代码的读者需要注意，二阶多项式核函数计算代价很高，在笔者的电脑上运行了数分钟之久。
$\qquad$ 在之前，我们用逻辑回归算法来处理乳腺癌检测问题时，使用二队多项式增加特征，同时使用 L1 范数作为正则项，其拟合效果比这里的支持向量机效果好。更重要的是，逻辑回归算法的运行效率远远高于二阶多项式核函数的支持向量机算法。当然，这里的支持向量机算法的效果还是比使用 L2 范数作为正则项的逻辑回归算法好的。由此可见，模型选择和模型参数调优，在工程实践中有着非常重要的作用的。
$\qquad$
$\qquad$