本文结构:
- 什么是感知器
- 有什么用
- 代码实现
1. 什么是感知器
在下图,这个神经网络中,每个圆圈都是一个神经元,神经元也叫做感知器
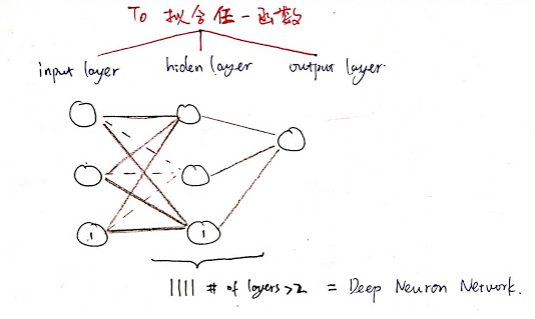
只有一个隐藏层的神经网络就能拟合任何一个函数,但它需要很多很多的神经元。
而深层神经网络用相对少的神经元就能拟合同样的函数,但是层数增加了,不太容易训练,需要大量的数据。
为了拟合一个函数,可以使用一个浅而宽的网络,也可以使用一个深而窄的网络,后者更节约资源。
举个例子
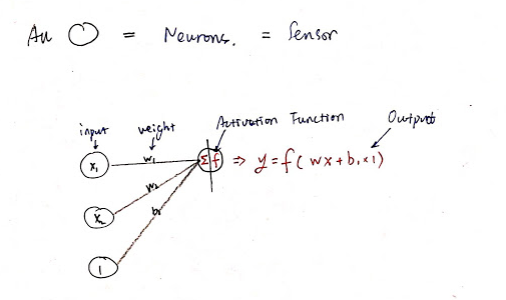
向一个感知器输入inputs,经过 加权 求和,再作用上激活函数,得到一个输出值
2. 有什么用
用感知器可以实现and函数,or函数,还可以拟合任何线性函数,任何线性分类或线性回归问题都可以用感知器来解决。
但是,感知器却不能实现异或运算,如下图所示,异或运算不是线性的,无法用一条直线把0和1分开。
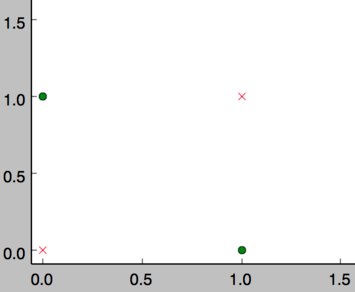
训练权重和偏置的算法如下:
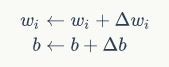
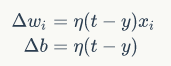
其中,t是训练样本的实际值,y是感知器的输出值,即由f计算出来的。η称为学习率,是个常数,作用是控制每一步调整权的幅度。
3. 代码实现
[main]
先训练and感知器
and_perception = train_and_perceptron()
得到训练后获得的权重和偏置
print(and_perception)
weights :[0.1, 0.2] bias :-0.200000
再去测试,看结果是否正确
print('1 and 1 = %d' % and_perception.predict([1, 1]))
其中
[train_and_perceptron]
先创建感知器,输入参数个数为2(因为and是二元函数),激活函数为f
p = Perceptron(2, f)
f为
def f(x):
return 1 if x > 0 else 0
输入训练data,迭代10次,学习速率为0.1
input_vecs, labels = get_training_dataset()
p.train(input_vecs, labels, 10, 0.1)
训练data为
input_vecs = [[1,1], [0,0], [1,0], [0,1]]
labels = [1, 0, 0, 0]
关于[train]
一共迭代10次,每次迭代时,先计算感知器在当前权重下的输出,然后更新weights
output = self.predict(input_vec)
self._update_weights(input_vec, output, label, rate)
其中[_update_weights]
就是用训练算法里面的两个公式
delta = label - output
self.weights = map(
lambda (x, w): w + rate * delta * x,
zip(input_vec, self.weights) )
self.bias += rate * delta

当[predict]
就用感知器的函数f:

return self.activator(
reduce(lambda a, b: a + b,
map(lambda (x, w): x * w,
zip(input_vec, self.weights))
, 0.0) + self.bias)

完整代码:
# -*-coding:utf-8-*-
import functools
import numpy as np
class Perception(object):
def __init__(self, input_num, activator):
'''
初始化感知器,设置输入参数的个数,以及激活函数。
激活函数的类型为 double -> double
'''
self.activator = activator
# 权重向量初始化为0
self.weights = [0.0 for _ in range(input_num)]
# 偏置项初始化为0
self.bias = 0.0
def __str__(self):
'''
打印学习到的权重、偏置项
'''
return 'weights\t:%s\nbias\t:%f\n' % (self.weights, self.bias)
def predict(self, input_vec):
'''
输入向量,输出感知器的计算结果
'''
# 把input_vec[x1, x2, x3, ...]和weights[w1, w2, w3, ...]打包在一起
# 变成[(x1, w1), (x2, w2), (x3, w3), ...]
# 然后利用map函数计算[x1*w1, x2*w2, x3*w3]
# 最后利用reduce求和
# 上面的方法适合python2,python3中没有reduce,并且lambda函数不支持如下写法:lambda (x, w)
# return self.activator(
# reduce(lambda a, b: a + b,
# map(lambda (x, w): x * w,
# zip(input_vec, self.weights))
# , 0.0) + self.bias)
return self.activator(
functools.reduce(lambda a, b: a + b,
map(lambda x_w: x_w[0] * x_w[1],
zip(input_vec, self.weights))
, 0.0) + self.bias)
def train(self, input_vecs, labels, iteration, rate):
'''
输入训练数据:一组向量、与每个向量对应的label;以及训练轮数、学习率
'''
for i in range(iteration):
self._one_iteration(input_vecs, labels, rate)
def _one_iteration(self, input_vecs, labels, rate):
'''
一次迭代,把所有的训练数据过一遍
'''
# 把输入和输出打包在一起,成为样本的列表[(input_vec, label), ...]
# 而每个训练样本是(input_vec, label)
samples = zip(input_vecs, labels)
# 对每个样本,按照感知器规则更新权重
for (input_vec, label) in samples:
# 计算感知器在当前权重下的输出
output = self.predict(input_vec)
# 更新权重
self._update_weights(input_vec, output, label, rate)
def _update_weights(self, input_vec, output, label, rate):
'''
按照感知器规则更新权重
'''
# 把input_vec[x1, x2, x3, ...]和weights[w1, w2, w3, ...]打包在一起
# 变成[(x1, w1), (x2, w2), (x3, w3), ...]
# 然后利用感知器规则更新权重
delta = label - output
self.weights = map(
lambda x_w: x_w[1] + rate * delta * x_w[0],
zip(input_vec, self.weights)
)
# 更新bias
self.bias += rate * delta
def f(x):
'''
定义激活函数f
'''
return 1 if x > 0 else 0
def get_training_dataset():
'''
基于and真值表构建训练数据
'''
# 构建训练数据
# 输入向量列表
input_vecs = [[1, 1], [0, 0], [1, 0], [0, 1]]
# 期望的输出列表,注意要与输入一一对应
# [1, 1] -> 1, [0, 0] -> 0, [1, 0] -> 0, [0, 1] -> 0
labels = [1, 0, 0, 0]
return input_vecs, labels
def train_and_perception():
'''
使用and真值表训练感知器
'''
# 创建感知器,输入参数个数为2(因为and是二元函数),激活函数为f
p = Perception(2, f)
# 训练,迭代10轮,学习速率为0.1
input_vecs, labels = get_training_dataset()
p.train(input_vecs, labels, 10, 0.1)
# 返回训练好的感知器
return p
if __name__ == '__main__':
# 训练and感知器
and_perception = train_and_perception()
# 打印训练获得的权重
print(and_perception)
# 测试
print('1 and 1 = %d' % and_perception.predict([1, 1]))
print('0 and 0 = %d' % and_perception.predict([0, 0]))
print('1 and 0 = %d' % and_perception.predict([1, 0]))
print('0 and 1 = %d' % and_perception.predict([0, 1]))
结果展示: