小白最优化学习（五）牛顿法（一）__ 最速下降法

先简单回顾下：

一、什么是最优化 引用

主要研究以下形式的问题：

给定一个函数 $f:A\to \mathbb{R}$ ，寻找一个元素 $\mathbf{x}^0\in A$ 使得对于所有 $A$ 中的 $\mathbf{x}$ ， $f(\mathbf{x}^0)\leq f(\mathbf{x})$ 或者 $f(\mathbf{x}^0)\geq f(\mathbf{x})$ 。

这类定式有时还称为“数学规划”（譬如，线性规划）。许多现实和理论问题都可以建模成这样的一般性框架。

典型的， $A$ 一般为欧几里得空间 $\mathbb{R}^n$ 中的子集，通常由一个 $A$ 必须满足的约束等式或者不等式来规定。 $A$ 的元素被称为是可行解。函数 $f$ 被称为目标函数，或者代价函数。一个最小化（或者最大化）目标函数的可行解被称为最优解。

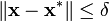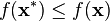一般情况下，会存在若干个局部的极小值或者极大值。局部极小值 $x^*$ 定义为对于一些 $\delta>0$ ，以及所有的 $x$ 满足 $\|\mathbf{x}-\mathbf{x}^*\|\leq\delta$ 使得公式 $f(\mathbf{x}^*)\leq f(\mathbf{x})$ 成立；这就是说，在 $\mathbf{x}^*$ 周围的一些闭球上，所有的函数值都大于或者等于在该点的函数值。一般的，求局部极小值是容易的，但是要确保其为全域性的最小值，则需要一些附加性的条件，例如，该函数必须是凸函数。

二、主要分支

线性规划

当目标函数f是线性函数而且集合A是由线性等式函数和线性不等式函数来确定的，我们称这一类问题为线性规划

整数规划

扫描二维码关注公众号，回复： 3705469 查看本文章

当线性规划问题的部分或所有的变量局限于整数值时，我们称这一类问题为整数规划问题

二次规划

目标函数是二次函数，而且集合A必须是由线性等式函数和线性不等式函数来确定的。

非线性规划

研究的是目标函数或是限制函数中含有非线性函数的问题。

随机规划

研究的是某些变量是随机变量的问题。

动态规划

研究的是最优策略基于将问题分解成若干个较小的子问题的优化问题。

组合最优化

研究的是可行解是离散或是可转化为离散的问题。

无限维最优化

研究的是可行解的集合是无限维空间的子集的问题，一个无限维空间的例子是函数空间。

三、牛顿法

1、最速下降法

最速下降法以梯度方向作为极小化算法的下降方向，又称梯度法，是无约束最优化中最简单的方法；

算法描述：

step 1 ：给出 $x_{0}$ ， $0<\varepsilon<1$ ，k:=0

step 2 ：计算 $d_{k}=-g_{k}$ ，如果 $\left \| g_{k} \right \| < \varepsilon$ 则停止（ $g_{k}=\bigtriangledown f(x_{k})$ ）

step 3 ：用一维搜索求出步长因子 $\alpha_{k}$ ，使得 $f(x_{k}+\alpha_{k}d_{k})=minf(x_{k}+\alpha d_{k})$

step 4 ：计算 $x_{k+1}=x_{k}+\alpha_{k}d_{k}$

step 5 ： $k:=k+1$ 并转至step 2

2、两点步长梯度法

基本思想是利用迭代当前点以及前一点的信息来确定步长因子

算法描述：

step 1 ：给出 $x_{0}$ ， $0<\varepsilon<1$ ，k:=0

step 2 ：计算 $d_{k}=-g_{k}$ ，如果 $\left \| g_{k} \right \| < \varepsilon$ 则停止（ $g_{k}=\bigtriangledown f(x_{k})$ ）

step 3 ：如果k==0，利用一维搜索哦求 $\alpha_{k}$ ，否则：

$a_{k}=s_{k-1}^{T}y_{k-1}/\left \| y_{k-1} \right \|^{2}$

或者 $a_{k}=\left \| s_{k-1} \right \|^{2}/s_{k-1}^{T}y_{k-1}$

step 4 ：计算 $x_{k+1}=x_{k}+\alpha_{k}d_{k}$

step 5 ： $k:=k+1$ 并转至step 2

一些说明

$x_{k+1}=x_{k}+\alpha_{k}g_{k}$ 可以看成 $x_{k+1}=x_{k}+D_{k}g_{k}$ ，其中 $D_{k}=\alpha_{k}I$ 是一个矩阵，为了使矩阵 $D_{k}=\alpha_{k}I$ 具有拟牛顿的性质

计算 $\alpha_{k}$ 使

$min\left \| s_{k-1}-D_{k}y_{k-1} \right \|$ 或者 $min\left \| D_{k}^{-1}s_{k-1}-y_{k-1} \right \|$

其中 $s_{k-1}=x_{k}-x_{k-1}$ ， $y_{k-1}=g_{k}-g_{k-1}$

小白最优化学习（五） 牛顿法（一）__ 最速下降法

猜你喜欢

小白最优化学习（五）牛顿法（一）__ 最速下降法