优化算法之——最速下降法

本文链接： https://blog.csdn.net/m0_37570854/article/details/88559619

引言：在解决无约束问题时，经常用到的一类算法是最速下降法，在求解机器学习算法的模型参数，即无约束优化问题时，梯度下降（Gradient Descent）是最常采用的方法之一，另一种常用的方法是最小二乘法。在求解损失函数的最小值时，可以通过梯度下降法来一步步的迭代求解，得到最小化的损失函数和模型参数值。反过来，如果我们需要求解损失函数的最大值，这时就需要用梯度上升法来迭代了。在机器学习中，基于基本的梯度下降法发展了两种梯度下降方法，分别为随机梯度下降法和批量梯度下降法。本节主要介绍一下最速下降法，并在最后运用matlab对其进行编程实现。(ps.推荐用电脑阅读，公式效果最佳)

1.原理

本篇主要讨论如下的优化模型：

$\underset{x\epsilon R^{2}}{min}f(x)$

其中 $f$ 是 $x$ 的实值连续函数，通常假定其具有二阶连续偏导数，对于 $maxf(x)$ 可以等价的转化为 $min(-f(x))$ ,所以下面仅讨论极小化问题。

最速下降法由于只考虑当前下降最快而不是全局下降最快，在求解非线性无约束问题时，最重要的是得到每一步迭代的方向 $d^{(k)}$ 和每一步下降的长度 $\lambda ^{_{(k)}}$ 。考虑到函数 $f(x)$ 在点 $x^_{(k)}$ 处沿着方向 $d$ 的方向导数 $f_{d}(x^{(k)})=\triangledown f(x^{(k)})^{T}d$ ,其意义是 $f(x)$ 在点 $x^{(k)}$ 处沿 $d$ 的变化率。当 $f$ 连续可微时，方向导数为负，说明函数值沿着该方向下降；方向导数越小（负值），表明下降的越快，因此确定搜索方向 $d^{(k)}$ 的一个想法就是以 $f(x)$ 在点 $x^{(k)}$ 方向导数最小的方向作为搜索方向。

1.1 搜索方向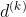 $d^{(k)}$ 的确定

设方向 $d$ 为单位向量， $\left \| d \right \|=1$ ,从点 $x^{(k)}$ 按方向 $d$ ,步长 $\lambda$ 进行搜索得到下一点 $x^{(k+1)}=x^{(k)}+\lambda_{k}d^{(k)}$ ，对该式进行泰勒展开得到：

$f(x^{(k)}+\lambda_{k} d^{(k)})=f(x^{(k)})+\lambda_{k} \triangledown f(x^{(k)})^{T}+o(\lambda )$

可以得到 $x^{(k)}$ 处的变化率：

$\lim_{t\rightarrow 0}\frac{f(x^{(k)}+\lambda_{k} d^{(k)})-f(x^{(k)}))}{\lambda_{k} }=\lim_{t\rightarrow 0}\frac{\lambda_{k} \triangledown f(x^{(k)})^{T}d^{(k)}+o(\lambda )}{\lambda_{k} }=\triangledown f(x^{(k)})^Td^{(k)}$

容易看出来在 $x^{(k)}$ 下降最快就是要在 $x^{(k)}$ 出的变化率最大，所以就是要使 $\triangledown f(x^{(k)})^Td^{(k)}$ 最小（ $\triangledown f(x^{(k)})^Td^{(k)}<0$ ）,而对于

$\triangledown f(x^{(k)})^Td^{(k)}=\left \|\triangledown f(x^{(k)}) \right \|\cdot \left \| d^{(k)} \right \|\cdot cos\theta$ ，要使其最小就是当 $cos\theta =-1$ 时，

$d^{(k)}=-\frac{\triangledown f(x^{(k)})}{\triangledown \left \| f(x^{(k)}) \right \|}$ ，即可以确定最速下降方向为 $-\triangledown f(x^{(k)})$ ,这也是最速下降法名字的由来。

1.2 步长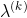 $\lambda^{(k)}$ 的确定

最速下降法采用的搜索步长通常采取的策略是精确步长搜索法，即： $\lambda_{k}=argminf(x^{(k)}+\lambda_{k}d^{(k)})$ ,通过求该式子的最小值点来求取步长，一般有：

$\frac{df(x^{(k)}+\lambda d^{(k)})}{d\lambda}=d^{(k)}\triangledown f(x^{(k)})=0$ ，该式表明 $d^{(k)}$ 和 $d^{(k+1)}$ 是正交的。在这里我没有用该方法，而是用一维搜索方法（黄金分割法<0.618法>）来近似找到最小值点，通过自己编程实现一维搜索更好的理解这个过程，最终的结果与精确搜索几乎一致。

2. 算法过程

求解问题： $\underset{x\epsilon R^{2}}{min}f(x)$

最速下降法的具体步骤为：

1. 选定初始点 $x^{(k)}$ ， $k=1$ ,给定精度要求 $\varepsilon >0$ 。

2.计算 $\triangledown f(x^{(k)})$ ，若 $\left \| \triangledown f(x^{(k)}) \right \|<\varepsilon$ ，则停止，否则令 $d^{(k)}=-\triangledown f(x^{(k)})$ ；

3. 在 $x^{(k)}$ 处沿方向 $d^{(k)}$ 作线搜索得 $x^{(k+1)}=x^{(k)}+\lambda_{k}d^{(k)}$ ， $k=k+1$ ，返回2.

3.例子

用最速下降法求解无约束非线性问题的最小值点：

$minf(x)=x_{1}^{2}+2x_{2}^{2}-2x_{1}x_{2}-2x_{2}$

其中 $x=(x_{1},x_{2})^{T},x^{(0)}=(0,0)^{T}$ 。

在这里为了直观的理解问题，我们对该问题进行可视化， $x_{1},x_{2}$ 分别取 $[-10,10]$ 步长为0.2。绘制图像如下：

解：在这里先用精确搜索求出最小值点，其后再用一维搜索进行验证。

（1） $\triangledown f(x)=(2x_{1}-2x_{2},4x_{2}-2x_{1}-2)^{T}$

（2） $\triangledown f(x^{(0)})=(0,-2)^{T}$

（3） $d^{(0)}=-\triangledown f(x^{(0)})=(0,2)^{T}$

（4）运用精确搜索求步长 $\lambda$

$\lambda=argminf(x^{(0)}+\lambda d^{(0)})$ ,可得 $\lambda=1/2$ ，

（5） $x^{(1)}=x^{(0)}+\lambda d^{(0)}=(0,1)^{T}$

同理转回（2）可以一直迭代回去一直到满足条件为止，得到最优解为 $x^{*}=(1,1)^{T}$ ， $y^{*}=-1$

4.优缺点

优点：
（1）每一步迭代简单，对初始点要求少
缺点：
（1）由于是对每一步进行最优迭代，但是整体的收敛下降速度不一定最快。
（2）用最速下降法求最优问题，迭代路径呈直角锯齿形如下图，开始的几步迭代很快，但越接近最优点收敛速度越慢

用matlab编程来求解，由于我在这里运用平分法确定极小值区间，然后用黄金分割法求的极小值，代码比较仔细，最终结果如下：

clear;
xk=[0,0]';
t=0.01;
syms x1;
syms x2;
while (1)
   [dfx1_value,dfx2_value]=steepest_gradient(xk);
   deltafx=[dfx1_value,dfx2_value]';
   gredfxabs=sqrt(dfx1_value.^2+dfx2_value.^2);
   if (gredfxabs<t)
      x_best=xk
      %f=x1-x2+2*x1.^2+2*x1*x2+x2.^2;
      f=x1.^2+2.*x2.^2-2.*x1.*x2-2.*x2;
      m=matlabFunction(f);
      y_best=m(xk(1),xk(2))
      break;
   else 
      dk=-deltafx;
      fx=lamdafunction(dk,xk);
      lamda=goldensfenge(fx);
      xk=xk-lamda*deltafx;
      continue;
   end
end

function [dfx1_value,dfx2_value]=steepest_gradient(xk)
syms x1;
syms x2;
%fx=x1.^2-2*x1*x2+4*x2.^2+x1-3*x2;
%fx=x1-x2+2*x1.^2+2*x1*x2+x2.^2;
fx=x1.^2+2.*x2.^2-2.*x1.*x2-2.*x2;
dfx_1=diff(fx,x1);
dfx_2=diff(fx,x2);
dfx1=matlabFunction(dfx_1);
dfx2=matlabFunction(dfx_2);
dfx1_value=dfx1(xk(1),xk(2));
dfx2_value=dfx2(xk(1),xk(2));

function [a,b]=region(fx,x0)
dx=0.1;
P=fdx(fx,x0);
if (P==0)
      x_best=x0; 
elseif (P>0)
    while (1)
      x1=x0-dx;
      dx=dx+dx;
      P=fdx(fx,x1);
      if(P==0)
          x_best=x1;
          break;
      elseif (P<0)
          a=x1;
          b=x0;
          break;
      else 
          x0=x1;
      end
    end
else
    while (1)
        x1=x0+dx;
        dx=dx+dx;
        P=fdx(fx,x1);
        if(P==0)
            x_best=x1;
            break;
        elseif(P>0)
            a=x0;
            b=x1;
            break;
        else
            x0=x1;
        end
    end
end

function fx=lamdafunction(dk,x_k)
syms lamda;
syms x1;
syms x2;
x1=x_k(1)+lamda*dk(1);
x2=x_k(2)+lamda*dk(2);
%fx=x1.^2-2*x1*x2+4*x2.^2+x1-3*x2;
%fx=x1-x2+2*x1.^2+2*x1*x2+x2.^2;
fx=x1.^2+2.*x2.^2-2.*x1.*x2-2.*x2;

function x_best=goldensfenge(fx)
x0=10*rand;
e=0.005;
[a,b]=region(fx,x0);
%x0=a+rand*(b-a);
 x1=a+0.382*(b-a);
 x2=a+0.618*(b-a);
 f1=fvalue(fx,x1);
 f2=fvalue(fx,x2);
while(1)
    if (f1>f2)
        a=x1;
        x1=x2;
        f1=f2;
        x2=a+0.618*(b-a);
        f2=fvalue(fx,x2);
        if(abs(b-a)<=e)
            x_best=(a+b)/2;
            break;
        else
            continue;
        end
    elseif(f1<f2)
        b=x2;
        x2=x1;
        f2=f1;
        x1=a+0.382*(b-a);
        f1=fvalue(fx,x1);
        if(abs(b-a)<=e)
            x_best=(a+b)/2;
            break;
        else
            continue;
        end
    else
        a=x1;
        b=x2;
        if(abs(b-a)<=e)
            x_best=(a+b)/2;
            break;
        else
            x1=a+0.382*(b-a);
            x2=a+0.618*(b-a);
            f1=fvalue(fx,x1);
            f2=fvalue(fx,x2);
            continue;
        end
    end
end

function y_value=fvalue(fx,a)
syms x;
%y=2*x.^2-x-1;
f=matlabFunction(fx);
y_value=f(a);

function dy_value=fdx(fx,a)
syms x;
%y=2*x.^2-x-1;
dy=diff(fx);
sign2fun=matlabFunction(dy);
dy_value=sign2fun(a);

编辑：高宇航