最速下降法基本介绍
在解决无约束问题时,经常用到的一类算法是最速下降法,在求解机器学习
算法的模型参数,即无约束优化问题时,梯度下降是最常采用的方法之一,在求
解损失函数的最小值时,可以通过梯度下降法来一步步的迭代求解,得到最小化
的损失函数和模型参数值。反过来,如果我们需要求解损失函数的最大值,这时
就需要用梯度上升法来迭代了。
讨论问题模型 minf(x)

步长的确定

算法步骤

求解例题
使用最速下降法求函数的最小值

程序代码(python)
import numpy as np
from sympy import *
import math
import matplotlib.pyplot as plt
import mpl_toolkits.axisartist as axisartist
x1, x2, t = symbols('x1, x2, t')
def func():
return pow(x1, 2) + 2 * pow(x2, 2) - 2 * x1 * x2 - 2 * x2
def grad(data):
f = func()
grad_vec = [diff(f, x1), diff(f, x2)]
grad = []
for item in grad_vec:
grad.append(item.subs(x1, data[0]).subs(x2, data[1]))
return grad
def grad_len(grad):
vec_len = math.sqrt(pow(grad[0], 2) + pow(grad[1], 2))
return vec_len
3
def zhudian(f):
t_diff = diff(f)
t_min = solve(t_diff)
return t_min
def main(X0, theta):
f = func()
grad_vec = grad(X0)
grad_length = grad_len(grad_vec)
k = 0
data_x = [0]
data_y = [0]
while grad_length > theta:
k += 1
p = -np.array(grad_vec)
X = np.array(X0) + t*p
t_func = f.subs(x1, X[0]).subs(x2, X[1])
t_min = zhudian(t_func)
X0 = np.array(X0) + t_min*p
grad_vec = grad(X0)
grad_length = grad_len(grad_vec)
print('grad_length', grad_length)
print('坐标', float(X0[0]), float(X0[1]))
data_x.append(X0[0])
data_y.append(X0[1])
print(k)
fig = plt.figure()
ax = axisartist.Subplot(fig, 111)
fig.add_axes(ax)
ax.axis["bottom"].set_axisline_style("-|>", size=1.5)
ax.axis["left"].set_axisline_style("->", size=1.5)
ax.axis["top"].set_visible(False)
ax.axis["right"].set_visible(False)
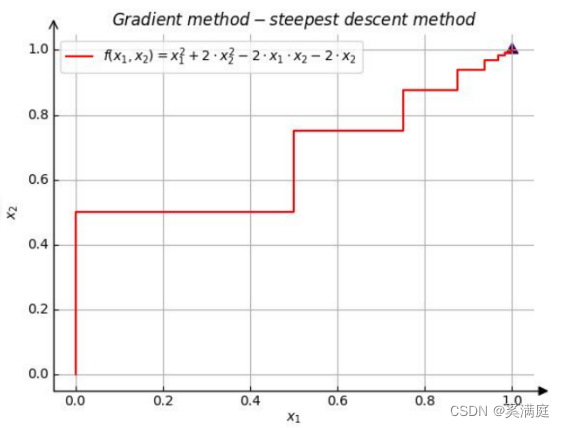
plt.title(r'$Gradient \ method - steepest \ descent \ method$')
plt.plot(data_x, data_y,color='r',label=r'$f(x_1,x_2)=x_1^2+2 \cdot
4
x_2^2-2 \cdot x_1 \cdot x_2-2 \cdot x_2$')
plt.legend()
plt.scatter(1, 1, marker=(3, 1), c=2, s=100)
plt.grid()
plt.xlabel(r'$x_1$', fontsize=20)
plt.ylabel(r'$x_2$', fontsize=20)
plt.show()
if __name__ == '__main__':
main([0, 0], 0.001)运行结果
grad_length 1.0
坐标
0.0 0.5
grad_length 1.0
坐标
0.5 0.5
grad_length 0.5
坐标
0.5 0.75
grad_length 0.5
坐标
0.75 0.75
grad_length 0.25
坐标
0.75 0.875
grad_length 0.25
坐标
0.875 0.875
grad_length 0.125
坐标
0.875 0.9375
grad_length 0.125
坐标
0.9375 0.9375
grad_length 0.0625
坐标
0.9375 0.96875
grad_length 0.0625
坐标
0.96875 0.96875
grad_length 0.03125
坐标
0.96875 0.984375
grad_length 0.03125
坐标
0.984375 0.984375
5
grad_length 0.015625
坐标
0.984375 0.9921875
grad_length 0.015625
坐标
0.9921875 0.9921875
grad_length 0.0078125
坐标
0.9921875 0.99609375
grad_length 0.0078125
坐标
0.99609375 0.99609375
grad_length 0.00390625
坐标
0.99609375 0.998046875
grad_length 0.00390625
坐标
0.998046875 0.998046875
grad_length 0.001953125
坐标
0.998046875 0.9990234375
grad_length 0.001953125
坐标
0.9990234375 0.9990234375
grad_length 0.0009765625
坐标
0.9990234375 0.99951171875
经过结果分析,每次迭代的结果坐标趋向于精确解
(1,1),
可以证明程序无误。
对运行结果绘制过程图