数据结构和算法：第八章 图论算法

9.1 若干定义

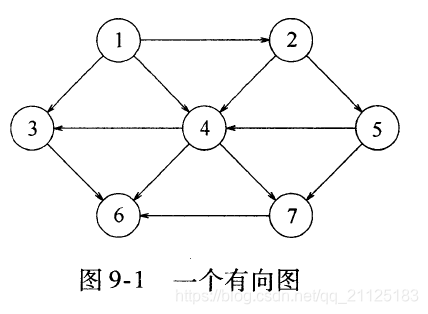
• 图的定义：一个图（Graph） G=(V,E)是由顶点的集合V和边Edge的集合E组成的。每一条边就是一个顶点对(v,w),其中(v,w) ∈E。有时候也把边叫做弧。如果顶点对是有序的，那么图就是有向的。有的图也叫做有向图。顶点w和顶点v邻接当且仅当(v,w)∈E。在一个具有边(v,w)从而具有边(w,v)的无向图中，w和v邻接且v和w邻接。有时候边还有第三种成分，成为权值。

• 图的路径：图中的一条路径是指一个顶点序列w1,w2,w3,w4…,wn使得(wi,wi+1)∈E，这样一条路径的长就是改路径的边的数量，它等于N-1。从一个顶点到它自身可以看做一个路径，如果路径不包含边，则该路径的长为0。一条简单路径就是这样一条路径，其上的所有顶点都是互异的，但第一个顶点和最后一个顶点可能相同

• 环：如果图含有一个顶点到它自身的边(v,v)，那么路径v，v叫做环。我们要讨论的图一般都是无环的。

• 有向图的圈：满足w1=wn，且至少长为1的一条路径;如果该路径是简单路径，那么这个圈就是简单圈。对于无向图来说，我们要求边是互异的。

• DAG有向无环图：如果一个有向图没有圈，那么这个有向图就是有向无环图。

---

• 连通性：如果一个无向图中从每个顶点到其他顶点都存在一个路径，那么这个无向图就是连通的。

• 强连通性：如果一个有向图中从每个顶点到其他顶点都存在一个路径，那么这个无向图就是强连通的。

• 若连通性：如果一个有向图不是强连通的，但是它的基础图（即其弧上去掉方向所形成的的图，）是连通的。那么该有向图就是弱连通图。

• 完全图：图中每一对顶点之间都存在一条边的图。

---

• 图的表示

若图是稠密的图，我们就可以采用邻接矩阵(使用一个二维数组)来表示这个图。对于每条边(v,w)，置A[u][v]等于true，否则这个数组的元素就是false。如果变有一个权值，那么就可以置这个权值为A[u][v]的值，而使用一个很大的值和一根小的值来表示不存在的边。

如图示稀疏的图，我们就可以采用邻接表来表示这个图。对于每一个顶点，我们使用一个表来存放这个顶点所有邻接的顶点。此时的空间需求为O(|E|+|V|)。

对于有几种方式保留邻接表。首先注意到的是，这些邻接表本身可以被保存在任何类的List中，即ArrayList和LinkedList中。然而，对于非常稀疏的图来说，当使用ArrayList的时候，程序员可能需要从一个比默认更小的容量开始ArrayList；否则可能会造成空间的浪费

还有一种方式就是使用一个映射，在这个映射下，关键字就是那些顶点，而他们的值就是那些邻接表，或者把一个邻接表作为Vetex类的数据成员保存下来。

9.2 拓扑排序

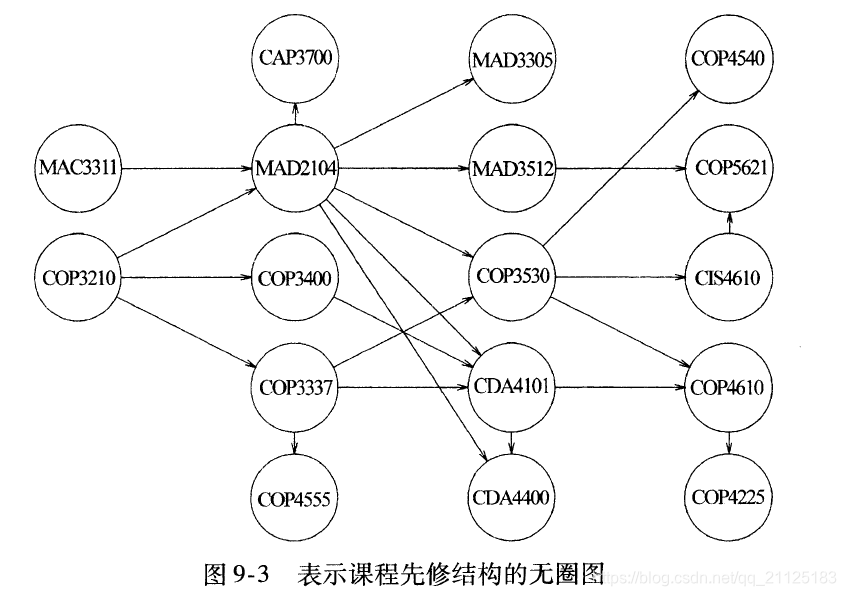
拓扑排序是对有向无圈图的顶点的一种排序，使得如果存在一条从vi到vj的路径，那么排序中vi就出现在vj的后面。

一个简单的拓扑排序的算法就是先找出任意一个没有入边的顶点。然后显示出该顶点，并将它从其边中删除。然后我们图的其他部分同样应用这样的方法。

• 入度：顶点v的入度定义为(u,v)的条数
• 出度：顶点u的出度定义为(u,v)的条数。

9.3 最短路径算法

---

• 单源最短路径

给定一个赋权图G = (V,E) 和一个特定顶点s作为输入，找出从s 到G中每一个其他顶点的最短赋权路径。

9.3.1 无权最短路径

广度优先遍历：该方法按层处理顶点：距开始最近的那些顶点首先被求值，而最远的那些顶点最后被求值。这很像树的层次遍历。

使用对拓扑排序的同样的分析，我们看到，只要是使用邻接表，则运行时间就是O(|E|+|v|)。

9.3.2 Dijkstra算法

如果是赋权图，那么问题无疑就变得非常困难了，不过我们仍然可以使用来自无权情形时的想法。

解决单源最短路径的一般方法叫做Dijkstra算法。Dijkstra算法按照阶段进行，正像无权最短路径算法一样。在每个阶段，Dijkstra算法选择一个顶点v，他在所有unknown顶点中具有最小的dv，同时算法声明从s到v的最短路径是known的。阶段的其余部分由dw的更新工作组成。

下面我们给出Dijkstra算法伪代码

Dijkstra算法 实现

public class Dijkstra {
    //创建地图
/*
 * S——16——>C—— 2——>D
 * | \     ^ ^     ^
 * 4  8    |  \    |
 * |    \  7   5   6
 * v     v |    \  |
 * A—— 3——>B—— 1——>E
 */

public static class Graph {

    Map<Character,List<Node>> map=new HashMap<Character,List<Node>>();//输出的地图

    public Graph() {
        List<Node> list=new ArrayList<Node>();
        list.add(new Node('S','A',4));
        list.add(new Node('S','B',8));
        list.add(new Node('S','C',16));
        list.add(new Node('A','B',3));
        list.add(new Node('B','C',7));
        list.add(new Node('B','E',1));
        list.add(new Node('C','D',2));
        list.add(new Node('E','C',5));
        list.add(new Node('E','D',6));

        for(int i=0;i<list.size();i++) {
            List<Node> temp = map.get(list.get(i).getSrc());
            if(temp==null)
                temp=new ArrayList<Node>();
            temp.add(list.get(i));
            map.put(list.get(i).getSrc(), temp);
        }
    }
}

public static class Node {
    private Character src;//起点
    private Character des;//终点
    private int len;      //距离长度
    private int path=Integer.MAX_VALUE;//初始设置为无穷长
    boolean known=false;    //访问过一次后就死亡

    public Node(){}

    public Node(Character src,Character des,int len) {
        this.src=src;
        this.des=des;
        this.len=len;
    }
    void setPath(int path) {
        this.path=path;
    }
    int getPath() {
        return path;
    }
    Character getSrc() {
        return src;
    }
    Character getDes() {
        return des;
    }
    int getLen() {
        return len;
    }
}

    public static Map<Character,Integer> dijkstra(Map<Character,List<Node>> map,Character c) {
        Queue<Node> heap=new LinkedList<Node>();

        //初始节点
        Node root=new Node(c,c,0);
        root.setPath(0);
        heap.add(root);

        Map<Character,Integer> result=new HashMap<Character,Integer>();

        while(!heap.isEmpty()) {
            Node x=heap.poll(),y = null;
            List<Node> temp=map.get(x.getDes());
            if(temp==null)
                continue;
            for(int i=0;i<temp.size();i++) {
                y=temp.get(i);
                if(y.getPath() > x.getDes()+y.getLen())
                    temp.get(i).setPath(x.getPath()+y.getLen());
                if(!temp.get(i).known) {
                    heap.add(temp.get(i));
                    temp.get(i).known=true;
                }
                if(result.get(temp.get(i).getDes())==null) {
                    result.put(temp.get(i).getDes(),temp.get(i).getPath());
                }
                if(result.get(temp.get(i).getDes())>temp.get(i).getPath()) {
                    result.put(temp.get(i).getDes(),temp.get(i).getPath());
                }
            }
        }
        return result;
    }

    public static void main(String[] argc)
    {
        Dijkstra.Graph graph=new Dijkstra.Graph();
        Map<Character,Integer> result=dijkstra(graph.map,'S');
        for(Map.Entry<Character,Integer> entry:result.entrySet())
        {
            System.out.println("S-->"+entry.getKey()+" 长度"+entry.getValue());
        }
    }
}

9.3.3 具有负边值的图

如果图负的边值，那么Dijkstra算法是行不通的。问题在于，一旦一个顶点被声明是known的，那么就可能从某个另外的unknown顶点v有一条回到u的负值的路径。

所以我们的解决方案就是，我们要忘记了关于unknown的顶点的概念，因为我们的算法要能够改变它的意向，下面是具有负值的赋值最短路径的伪代码：

9.3.4 无圈图

如果我们知道图是无圈的，那么我们可以通过改变声明顶点known的顺序，或者叫作顶点选取法则，来改进Dijkstra算法。新法则是以拓扑顺序选择顶点。由于选择和更新可以在拓扑排序执行的时候进行，因此算法可以一趟完成。

因为当一个顶点被选取以后，按照拓扑排序的法则它没有从known顶点发出的进入边，因此它的距离dv可以不再被降低，所以这种选取法则是行的通的。

无圈图的一个更重要的应用就是关键路径法。我们用如下动作节点图作为一个例子。每个节点表示一个必须执行的动作以及完成动作所要花费的时间。因此，该图叫做动作节点图。

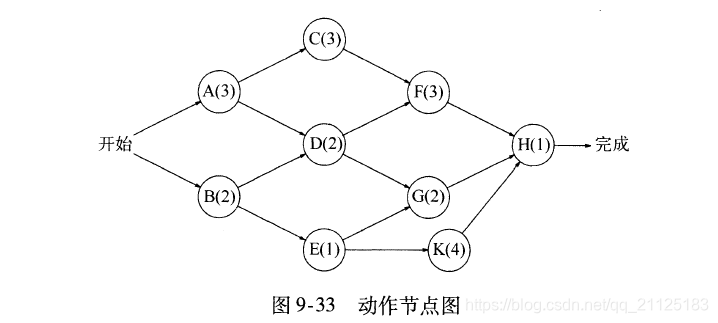
9.4 最小生成树问题

最小生成树问题：一个无向图的最小生成树就是由该图的那些连接G的所有顶点的边构成的树，且总价值是最小的。

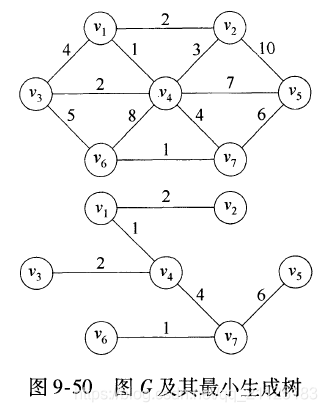
上面图中最小生成树种的边的条数为（|V|-1）

9.4.1 Prim算法

算法思想：在算法的任意时刻，我们都可以看到一组已经添加到树上的顶点，而其余顶点尚未添加到这个树中。此时，算法在每一个阶段都可以通过(u,v)使得(u,v)中的值是所以u在树上但v不在树上的边的值中的最小者而找出一个新的顶点并把它添加到这可树中。

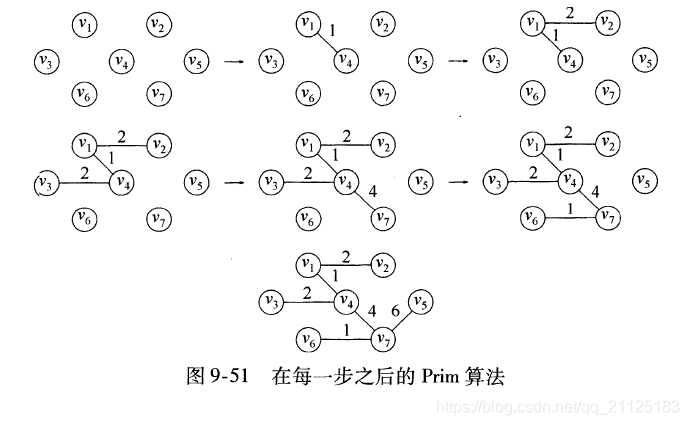
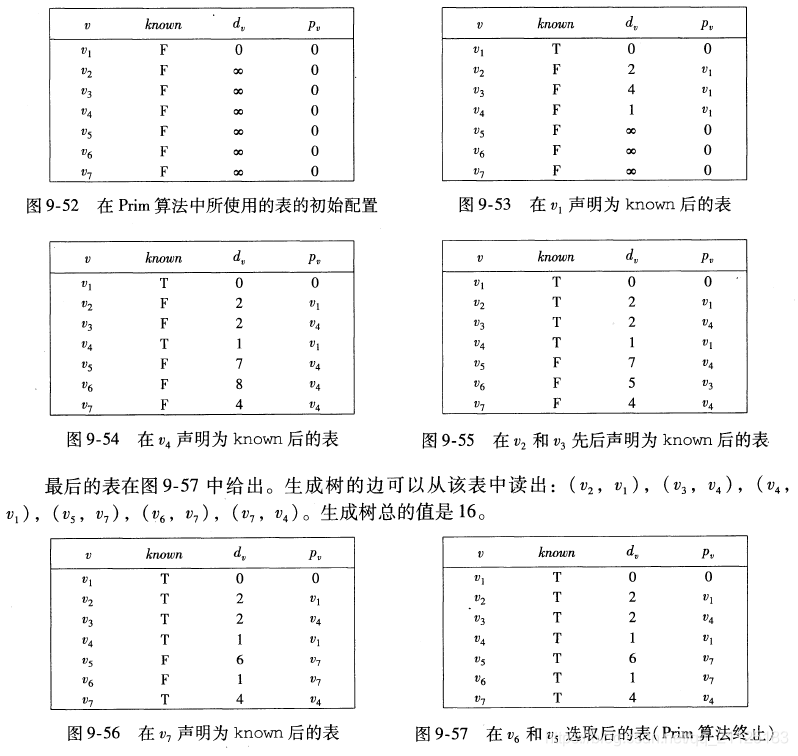
这个算法的实现和Dijkstra算法是一样的，对于Dijkstra算法分析所做的一件事都可以用到这里。

9.4.2 Kruskal算法

Kruskal算法的贪婪策略就是联系按照最小的权值选择边，并且当所选的边不产生圈的时候就把他作为所选取的边。

形式上，Kruskal算法就是在处理一个深林----树的集合。开始的时候，存在|V|颗单节点的树，而添加一边就可以将两颗树合并成一颗树。当算法终止的时候，就只有一颗树了，这棵树就是最小生成树。

9.5 深度优先搜索的应用

深度优先遍历是对先序遍历的推广。我们从某个顶点u开始出来v，然后递归地开始遍历所有与v邻居的顶点。我们对任意的图进行该过程，那么我们要小心仔细的避免圈的出现。为此，当访问一个顶点v的时候，由于我们当时已经到了该点处，因此可以标记该点是访问过的，并且对于尚未被标记的所有邻居顶点来说递归调用深度优先遍历。

9.5.1 无向图

深度优先搜索的伪代码：