前言:
终于放寒假了,在家休息几天然后查了下考研学校后,打算开始写总结了。原因很简单,刷过的好多题都忘了,打算二刷顺便写下总结。引用名言:“学而不思则罔,思而不学则殆。”所以在做题的同时,我们需要更多的思考,这样才能把知识完全学懂,今日总结的主题是《二叉搜索树》。
二叉搜索树的定义及性质:
二叉搜索树(英语:Binary Search Tree),也称为二叉查找树、有序二叉树(ordered binary tree)或排序二叉树(sorted binary tree),是指一棵空树或者具有下列性质的二叉树:
- 1)每个节点中的值必须大于(或等于)存储在其左侧子树中的任何值。
- 2)每个节点中的值必须小于(或等于)存储在其右子树中的任何值。
- 3)任意节点的左右子树也是二叉搜索树。
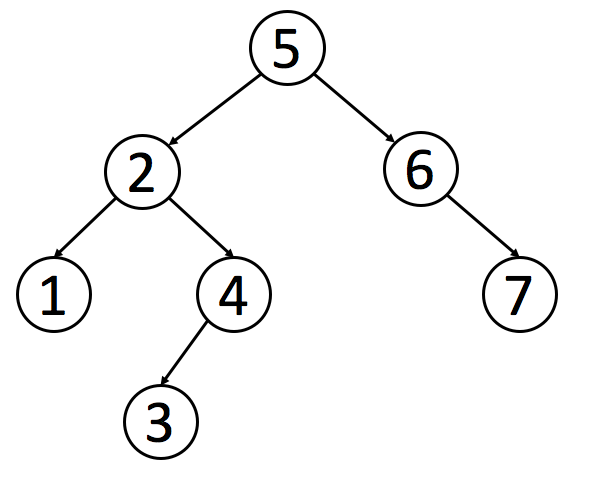
二叉搜索树与二叉树的关系:
二叉搜索树也是一颗二叉树,只不过是需要满足它三点性质的二叉树。对于二叉搜索树,我们也可以利用层序遍历、前序遍历,中序遍历、后序遍历来遍历它,但是值得注意的是二叉搜索树的中序遍历(左根右)遍历出来的结果是一个有序数组,也可将二叉搜索树的所有节点值映射到一条水平直线上,得到结果也将是一个有序数组。
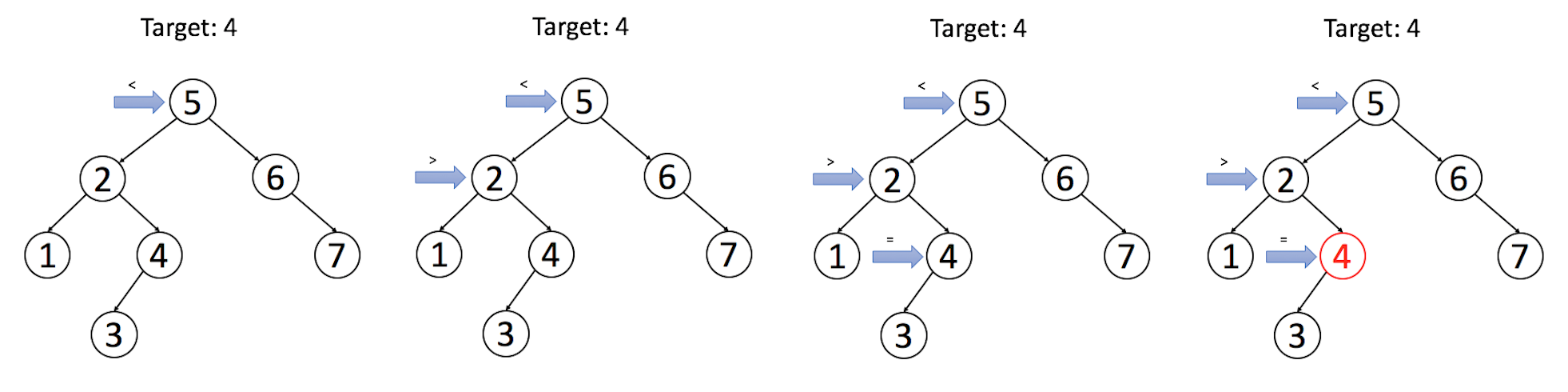
二叉搜索树的搜索操作:
1)如果目标值等于节点的值,则返回节点;
2)如果目标值小于节点的值,则继续在左子树中搜索;
3)如果目标值大于节点的值,则继续在右子树中搜索。
代码如下:
/*搜索节点值*/
TreeNode* searchBST(TreeNode* root, int val) {
if(root==nullptr)return root;
//1、找到目标值,返回该节点
if(root->val==val)return root;
//2、目标值小于该节点的值,则在左子树中寻找
else if(root->val>val)return searchBST(root->left,val);
//3、目标值大于该节点的值,则在右子树中寻找
else return searchBST(root->right,val);
}
二叉树的插入操作:
由于二叉树的插入操作有多种,比如:有改变原树结构的插入;也有根据搜索方式选择合适的叶子节点进行插入新节点。在这里我们主要使用后一种方法进行插入。
1)根据节点值与目标节点值的关系,搜索左子树或右子树;
2)重复步骤 1 直到到达外部节点(空节点);
3)根据节点的值与目标节点的值的关系,将新节点添加为其左侧或右侧的子节点。
代码如下:
//递归版:插入节点值
TreeNode* insertIntoBST_1(TreeNode* root, int val) {
if(root==nullptr)return new TreeNode(val);
else
{
//val的值小于根节点的值,要插在左边,递归直到左边的叶子节点时,将val的节点添加到最左边叶子节点的left节点
if(val<root->val)root->left=insertIntoBST_1(root->left,val);
//val的值大于根节点的值,要插在右边,递归直到右边的叶子节点时,将val的节点添加到最右边叶子节点的right节点
if(val>root->val)root->right=insertIntoBST_1(root->right,val);
}
return root;
}
二叉树的删除操作:
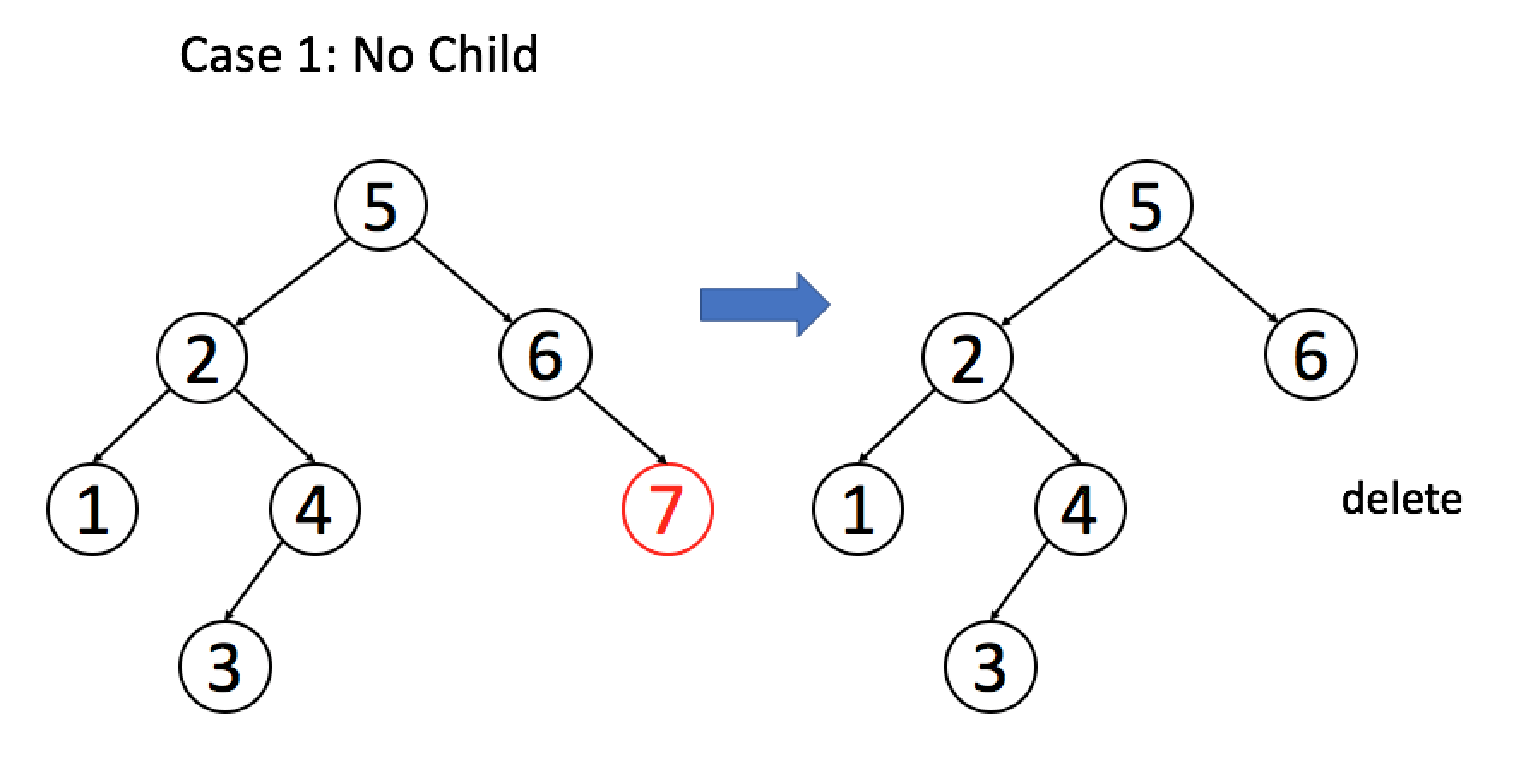
删除要比我们前面提到过的两种操作复杂许多。有许多不同的删除节点的方法,我们只讨论一种使整体操作变化最小的方法。我们的方案是用一个合适的子节点来替换要删除的目标节点。根据其子节点的个数,我们需考虑以下三种情况:
- 1)如果目标节点没有子节点,我们可以直接移除该目标节点。
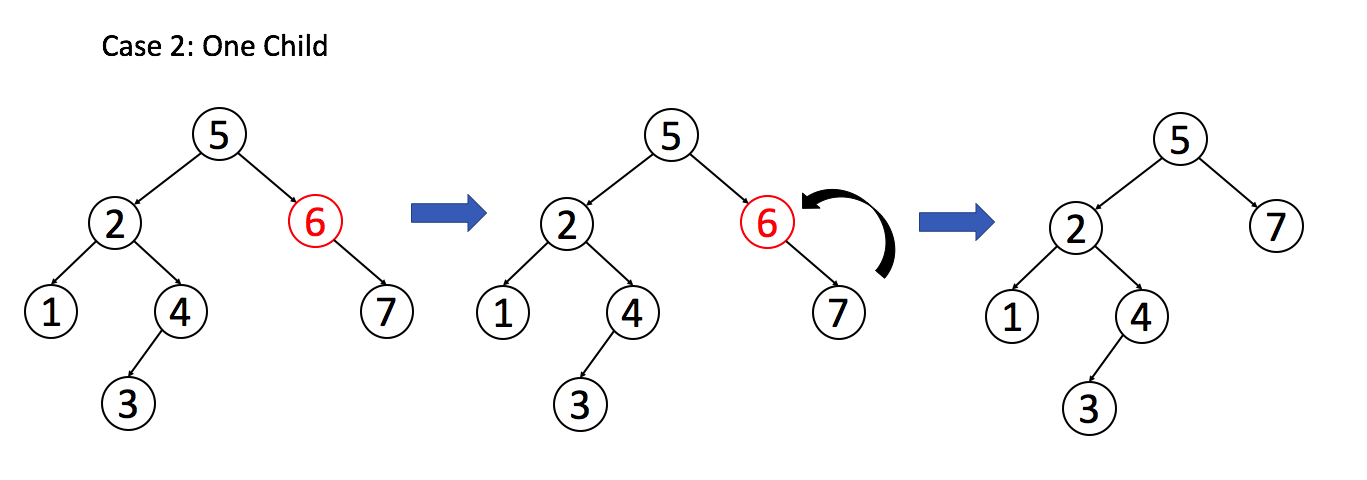
- 2)如果目标节只有一个子节点,我们可以用其子节点作为替换。
- 3)如果目标节点有两个子节点,我们需要用其中序后继节点或者前驱节点来替换,再删除该目标节点。
代码如下:
//第一种方法删除节点:我们将删除节点的右子树连接在其左子树的最右节点上面,然后返回左子树
TreeNode* deleteNode_1(TreeNode* root, int key) {
if(root==nullptr)return nullptr;
if (root->val==key)//找到需要删除的节点
{
if (root->left)
{//遍历需要删除节点的左子树,找到该左子树的最右边节点,也就是整个左子树中的最大值,然后将删除的节点的右子树连接到最右边节点上,返回左子树
//这句话的意思是说:我们将需要删除节点的右子树连接在其左子树的最右节点上面,因为右子树的最小值根节点也会大于左子树的最大值(最右节点)
TreeNode* node = root->left;
while (node->right) node = node->right;
node->right = root->right;
return root->left;
}
//左子树为空,直接将右子树节点替换到删除节点上
return root->right;
}
if (root->val>key)root->left = deleteNode_1(root->left, key);
else root->right = deleteNode_1(root->right, key);
return root;
}
//第二种删除节点的方法:我们将删除节点的左子树连接在其右子树的最左节点上
TreeNode* deleteNode_2(TreeNode* root,int key)
{
if(root==nullptr)return nullptr;
if(root->val==key)
{
if(root->right)
{//遍历删除节点的右子树,找到该右子树的最左边节点,也就是整个右子树中的最小值,然后将删除节点的左子树连接到最左边节点上,返回右子树
//因为删除节点左子树的所有节点都小于删除节点,而删除节点的右子树的所有节点都大于删除节点,所以右子树中的最小节点值也会大于左子树中的最大节点值
TreeNode* node=root->right;
while(node->left)node=node->left;
node->left=root->left;
return root->right;
}
return root->left;
}
if(root->val>key)root->left = deleteNode_2(root->left, key);
else root->right = deleteNode_2(root->right, key);
return root;
}
二叉搜索树的模板:
class BST
{
private:
/*节点*/
struct TreeNode
{
int val;
TreeNode *left, *right;
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};
TreeNode* root;
private:
//递归版:搜索节点值
TreeNode* searchBST_1(TreeNode* root, int val) {
if(root==nullptr)return root;
if(root->val==val)return root;
else if(root->val>val)return searchBST_1(root->left,val);
else return searchBST_1(root->right,val);
}
//迭代版:搜索节点值
TreeNode* searchBST_2(TreeNode* root,int val){
while(root){
if(root->val==val)return root;
else if(val<root->val)root=root->left;
else root=root->right;
}
return nullptr;
}
//递归版:插入节点值
TreeNode* insertIntoBST_1(TreeNode* root, int val) {
if(root==nullptr)return new TreeNode(val);
else
{
//val的值小于根节点的值,要插在左边,递归直到左边的叶子节点时,将val的节点添加到最左边叶子节点的left节点
if(val<root->val)root->left=insertIntoBST_1(root->left,val);
//val的值大于根节点的值,要插在右边,递归直到右边的叶子节点时,将val的节点添加到最右边叶子节点的right节点
if(val>root->val)root->right=insertIntoBST_1(root->right,val);
}
return root;
}
//迭代版:插入节点值
TreeNode* insertIntoBST_2(TreeNode* root,int val){
if(!root)return new TreeNode(val);
TreeNode* p=root;
while(p){
if(val<p->val){//在左子树中寻找叶子节点进行插入
if(!p->left){//找到叶子节点,插入到叶子节点后面
p->left=new TreeNode(val);
return root;
}
p=p->left;
}
else{//在右子树中寻找叶子节点进行插入
if(!p->right){//找到叶子节点,插入到叶子节点后面
p->right=new TreeNode(val);
return root;
}
p=p->right;
}
}
return root;
}
//第一种方法删除节点:我们将删除节点的右子树连接在其左子树的最右节点上面,然后返回左子树
TreeNode *deleteNode_1(TreeNode* root, int key)
{
if (root == nullptr)
return nullptr;
if (root->val == key) //找到需要删除的节点
{
if (root->left)
{ //遍历需要删除节点的左子树,找到该左子树的最右边节点,也就是整个左子树中的最大值,然后将删除的节点的右子树连接到最右边节点上,返回左子树
//这句话的意思是说:我们将需要删除节点的右子树连接在其左子树的最右节点上面,因为右子树的最小值根节点也会大于左子树的最大值(最右节点)
TreeNode *node = root->left;
while (node->right)
node = node->right;
node->right = root->right;
return root->left;
}
//左子树为空,直接将右子树节点替换到删除节点上
return root->right;
}
if (root->val > key)
root->left = deleteNode_1(root->left, key);
else
root->right = deleteNode_1(root->right, key);
return root;
}
//第二种删除节点的方法:我们将删除节点的左子树连接在其右子树的最左节点上
TreeNode *deleteNode_2(TreeNode* root, int key)
{
if (root == nullptr)
return nullptr;
if (root->val == key)
{
if (root->right)
{ //遍历删除节点的右子树,找到该右子树的最左边节点,也就是整个右子树中的最小值,然后将删除节点的左子树连接到最左边节点上,返回右子树
//因为删除节点左子树的所有节点都小于删除节点,而删除节点的右子树的所有节点都大于删除节点,所以右子树中的最小节点值也会大于左子树中的最大节点值
TreeNode *node = root->right;
while (node->left)
node = node->left;
node->left = root->left;
return root->right;
}
return root->left;
}
if (root->val > key)
root->left = deleteNode_2(root->left, key);
else
root->right = deleteNode_2(root->right, key);
return root;
}
//中序遍历:得到排序数组
vector<int> inorderTraversal(TreeNode* root) {
if(nullptr==root) return {};
vector<int> result;
stack<TreeNode*> recond;
while(!recond.empty()||root!=nullptr)
{
if(root!=nullptr)//进栈顺序为根左...根左,出栈顺序为左根...左根
{
recond.push(root);
root=root->left;
}
else//直至上一结点的左结点为nullptr时,将上一结点的val打印,并添加其右子树
{
TreeNode* top=recond.top();recond.pop();
result.push_back(top->val);
root=top->right;
}
}
return result;
}
public:
BST():root(nullptr){}
TreeNode* searchBST_1(int val){
return searchBST_1(root,val);
}
TreeNode* searchBST_2(int val){
return searchBST_2(root,val);
}
TreeNode* insertIntoBST_1(int val){
root=insertIntoBST_1(root,val);
return root;
}
TreeNode* insertIntoBST_2(int val){
root=insertIntoBST_2(root,val);
return root;
}
TreeNode* deleteNode_1(int key){
root=deleteNode_1(root,key);
return root;
}
TreeNode* deleteNode_2(int key){
root=deleteNode_2(root,key);
return root;
}
vector<int> inorderTraversal(){
return inorderTraversal(root);
}
};
二叉搜索树的时间复杂度:
二叉查找树相比于其他数据结构的优势在于查找、插入的时间复杂度较低,为O(log n)。二叉查找树是基础性数据结构,用于构建更为抽象的数据结构,如集合、多重集、关联数组等。
二叉查找树的查找过程和次优二叉树类似,通常采取二叉链表作为二叉查找树的存储结构。中序遍历二叉查找树可得到一个关键字的有序序列,一个无序序列可以透过建构一棵二叉查找树变成一个有序序列,建构树的过程即为对无序序列进行查找的过程。每次插入的新的结点都是二叉查找树上新的叶子结点,在进行插入操作时,不必移动其它结点,只需改动某个结点的指针,由空变为非空即可。搜索、插入、删除的复杂度等于树高,期望O(log n),最坏O(n)(数列有序,树退化成线性表)。
虽然二叉查找树的最坏效率是O(n),但它支持动态查询,且有很多改进版的二叉查找树可以使树高为O(log n),从而将最坏效率降至O(log n)。
二叉搜索树相关题目:
95. 不同的二叉搜索树 II:主要利用二叉搜索树的性质进行分治法,以根节点i为分界点,分别求出左子树的节点集合[1,i-1],右子树的节点集合[i+1,n],然后再两两组合左右子树的节点,形成最终结果。分治法的最小子问题为区间内没有元素时,最小子问题得解,左右子树节点集合也得解了。
96. 不同的二叉搜索树:这道题其实和二叉搜索树没有多大关系,主要考察数学公式及推导,所以大家不会做很正常,下次碰到知道怎么做就行了。重点记一下卡特兰数的第一个公式就好。
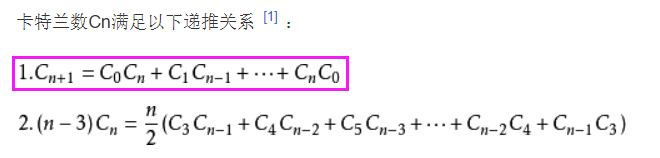
98. 验证二叉搜索树:用类似中序遍历(左根右)的方式来验证是否为二叉搜索树,若左子树的值大于等于根节点的值,则返回false;若根结点的值大于等于右子树的值,则返回false。
108. 将有序数组转换为二叉搜索树:由于有序数组的中位数为二叉搜索树的根节点,所以我们需要根据有序数组的中位数来划分左右子树,然后利用递归将根节点连接左右子树即可。
173. 二叉搜索树迭代器:仅仅将中序遍历最小值之前的节点压入栈中,当next时我们将栈顶元素取出即为最小值返回,当然在此之前需要将下一个最小值找到,并将路径上的所有节点压入栈中以供使用,查看是否迭代到头只需判断栈是否为空即可。
230. 二叉搜索树中第K小的元素:直接利用中序遍历,返回第k个节点值即可,注意要用一个计数器count,计算是否到第k个节点。
235. 二叉搜索树的最近公共祖先:充分利用二叉搜索数的性质,若pq都在左子树中,我们需要在左子树寻找最近公共祖先;若pq都在右子树中,我们需要在右子树中寻找最近公共祖先;若pq分别在左右子树中,那么此时的根节点就是就是最近公共祖先。
530. 二叉搜索树的最小绝对差:利用中序遍历将二叉搜索树转换为一个升序数组,然后遍历这个数组,计算差的绝对值。
501. 二叉搜索树中的众数:二叉搜索树的中序遍历是一个升序序列,逐个比对当前结点(root)值与前驱结点(pre)值。更新当前节点值出现次数(curTimes,初始化为1)及最大出现次数(maxTimes),更新规则:若curTimes=maxTimes,将root->val添加到结果向量(res)中;若curTimes>maxTimes,清空res,将root->val添加到res,并更新maxTimes为curTimes。
1305. 两棵二叉搜索树中的所有元素:直接利用树的前序遍历将两课树的所有节点值存放在一个数组中,然后将数组排序输出就好了。