【通信原理 入坑之路】—— 利用MatLAB绘制 QPSK 调制波形及其包络分析

一、QPSK 调制信号的平面波形绘制

在写 $code$ 之前，我们先明确 $QPSK$ 调制的过程（用实数运算实现）：

1. 输入一串二进制比特序列（经过信源编码、信道编码和交织之后的结果）
2. 这个二进制比特序列经过一个星座图映射，对于 $QPSK$ 调制的映射关系，如下所示：

二进制序列	IQ信号	$s(t)$相位
00	$+\frac{1}{\sqrt{2}}$, $+\frac{1}{\sqrt{2}}$	$\frac{Π}{4}$
01	$-\frac{1}{\sqrt{2}}$, $+\frac{1}{\sqrt{2}}$	$\frac{3Π}{4}$
11	$-\frac{1}{\sqrt{2}}$, $-\frac{1}{\sqrt{2}}$	$\frac{5Π}{4}$
10	$+\frac{1}{\sqrt{2}}$, $-\frac{1}{\sqrt{2}}$	$\frac{7Π}{4}$

3. 经过映射得到的 $I$ 路、 $Q$ 路信号，我们让他们分别经过脉冲成型滤波器（升余弦滚降滤波器）
4. 将经过滤波器的波形分别和对应的 $cos$ 和 $sin$ 载波相乘，然后相减得到调制后的信号

上述过程用负数运算一样可以实现，而且用复数运算的情况更多：

1. 和步骤1，2一样，也是先得到映射之后的 $I, Q$ 两路信号，我们组成复信号： $I + jQ$
2. 我们把载波也组成复信号： $cos(2Πf_ct) + jsin(2Πf_ct)$
3. 将这两个复信号相乘，再取实部，就得到调制之后的信号。

我们先用实数运算实现一下：

subplot(4,1,1);
%%%第一个图先画输入的二进制比特序列%%%
t = 0:0.001:8;     
d = [0 0;0.5 1;1 1;1.5 0;2 1;2.5 1;3 0;3.5 0;4 1;4.5 0;5 1;5.5 1;6 0;6.5 1;7 0;7.5 0];
message = pulstran(t-0.25, d, 'rectpuls', 0.5);
plot(t, message);
axis([0 8 -0.2 +1.2]);

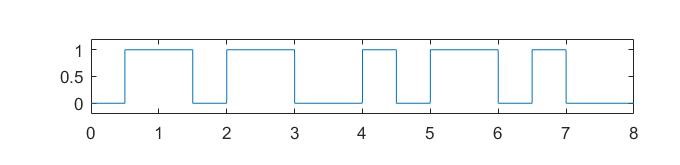
其中， $pulstran$ 函数用于生成连续或离散的脉冲串； $d$ 数组的第一列是某一时刻，第二列是该时刻对应的二进制序列的值。

下面分别绘制 $I$ , $Q$ 两路信号。

%%%下面分别绘制映射+脉冲成型之后的I, Q信号%%%
subplot(4,1,2);
a = 1/sqrt(2);
x = t-0.5;           %因为我们设采样时刻在 kTs+0.5,也就是每一个码元持续时间的中间
I1 = -a.*sinc(x).*cos(pi*x)./(1-4.*x.*x);
x = t-1.5;             %第二个时刻的码元输入升余弦滚降滤波器
I2 = a.*sinc(x).*cos(pi*x)./(1-4.*x.*x);
x = t-2.5;
I3 = -a.*sinc(x).*cos(pi*x)./(1-4.*x.*x);
x = t-3.5;
I4 = a.*sinc(x).*cos(pi*x)./(1-4.*x.*x);
x = t-4.5;
I5 = a.*sinc(x).*cos(pi*x)./(1-4.*x.*x);
x = t-5.5;
I6 = -a.*sinc(x).*cos(pi*x)./(1-4.*x.*x);
x = t-6.5;
I7 = -a.*sinc(x).*cos(pi*x)./(1-4.*x.*x);
x = t-7.5;
I8 = a.*sinc(x).*cos(pi*x)./(1-4.*x.*x);
I = I1+I2+I3+I4+I5+I6+I7+I8;
plot(t, I);
title('I signal');

Q路：

subplot(4,1,3);
x = t-0.5;           %因为我们设采样时刻在 kTs+0.5,也就是每一个码元持续时间的中间
Q1 = a.*sinc(x).*cos(pi*x)./(1-4.*x.*x);
x = t-1.5;             %第二个时刻的码元输入升余弦滚降滤波器
Q2 = -a.*sinc(x).*cos(pi*x)./(1-4.*x.*x);
x = t-2.5;
Q3 = -a.*sinc(x).*cos(pi*x)./(1-4.*x.*x);
x = t-3.5;
Q4 = a.*sinc(x).*cos(pi*x)./(1-4.*x.*x);
x = t-4.5;
Q5 = -a.*sinc(x).*cos(pi*x)./(1-4.*x.*x);
x = t-5.5;
Q6 = -a.*sinc(x).*cos(pi*x)./(1-4.*x.*x);
x = t-6.5;
Q7 = a.*sinc(x).*cos(pi*x)./(1-4.*x.*x);
x = t-7.5;
Q8 = a.*sinc(x).*cos(pi*x)./(1-4.*x.*x);
Q = Q1+Q2+Q3+Q4+Q5+Q6+Q7+Q8;
plot(t, Q);
title('Q signal');

接下来，我们要做的就是分别将 $I$ 路信号和 $Q$ 路信号和对应 $cos$ 与 $sin$ 载波相乘。然后，取： $s(t) = Icos - Qsin$，为了便于观察，我们只是取载波频率为 10 Hz。当然实际频率比这个大得多得多。

subplot(4,1,4);
fc = 10;
I_carrier = cos(2*pi*fc*t);
Q_carrier = sin(2*pi*fc*t);
st = I.*I_carrier - Q.*Q_carrier;
plot(t, st);
title('modulated signal');

因此，上述所有代码的效果图如下所示：

下面画一下这个调制信号 $s(t)$ 的包络线，先来看看信号包络是啥：
“将一段时间长度的高频信号的峰值点连线，就可以得到上方（正的）一条线和下方（负的）一条线，这两条线就叫包络线。包络线就是反映高频信号幅度变化的曲线。”

figure(2);
fc = 10;
I_carrier = cos(2*pi*fc*t);
Q_carrier = sin(2*pi*fc*t);
st = I.*I_carrier - Q.*Q_carrier;
plot(t, st);
hold on;
envelope = sqrt(I.^2 + Q.^2);
plot(t, envelope, 'r');
hold on;
plot(t, -envelope, 'r');

从定义我们也知道：这个高频信号的表达式是， $s(t) = Icos(2Πf_ct) - Qsin(2Πf_ct)$
因此，这个高频信号的峰值可以写成： $\sqrt{I^2 +Q^2}$

又因为映射之后的比特信息要经过升余弦滚降滤波器，因此， $I$， $Q$信号也是一个随时间变化的函数，因此，高频信号的峰值也是一个随时间变化的函数了正如图中红色线所示。

有由于我们在前面的 $Blog$ 中，提到 IQ 调制是正交调制。为什么呢？如果我们把 $I$ 路信号看成实轴上的分量、 $Q$ 路信号看成是虚轴上的分量，那么就可以合成一个向量： $I + jQ$，如下图：

然后和复数 $e^{j2Πf_ct}$ 相乘，模值不变，只是一直在旋转，这个旋转向量在实轴上的投影，就是调制之后的信号。

可以现在呢？由于加入了升余弦滚降滤波器，我们得到的 $I$， $Q$ 信号都是幅度随时间变化的信号了，那么它们两个合成的向量 $I+jQ$，也就是模值随时间变化的向量了。不仅如此，由于 $I$， $Q$信号有时候会反向，就会导致 $I+jQ$ 信号的相位也会随时间变化。

因此，我们照着这个思路画一下 现在复信号 $I+jQ$ 和 复信号 $cos + jsin$ 的乘积旋转向量随时间变化的情况：

figure(3);
j = sqrt(-1);
t =  0:0.001:8;   
complex_I_Q = I + j.*Q;
complex_carrier = I_carrier + j.*Q_carrier;
st_complex = complex_I_Q.*complex_carrier;
plot3(real(st_complex), t, imag(st_complex));
ylabel('t');
zlabel('y');
xlabel('x');
set(gca,'YDir','reverse');
axis([-1.5 1.5 0 8 -1.5 1.5]);
grid on;

为什么复信号 $s(t) = (I+jQ)(cos+jsin)$ 在空间中长这样呢？原因很简单，我们知道： $cos(2Πf_ct) + jsin(2Πf_ct) = e^{j2Πf_ct}$
而 $e^{j2Πf_ct}$ 的图像长这样：

figure(4);
fc = 1;
t=-5:0.001:5;
x=cos(2*pi*fc*t);
y=sin(2*pi*fc*t);
plot3(x,t,y);
xlabel('x');
ylabel('t');
zlabel('y');
set(gca,'YDir','reverse');
grid on;
title('e^{j\omega_0t}的波形');

这里为了便于观察，我选择了载波频率为 1Hz。

而这个旋转复指数信号的幅值是 $\sqrt{I^2+Q^2}$，这是一个随时间变化的函数，因此，最终这个复指数信号的幅度也会随着时间不断变化。