【通信原理 入坑之路】 —— 深入理解BPSK调制和解调的全过程及其Matlab实现

写在前面：本博文是《深入浅出通信原理》的学习笔记，加之本人自我理解撰写而成，仅供个人学习使用

一、BPSK调制过程

还记得我们在之前的博文中提到的IQ调制吗？我们再来熟悉一下IQ调制的流程：

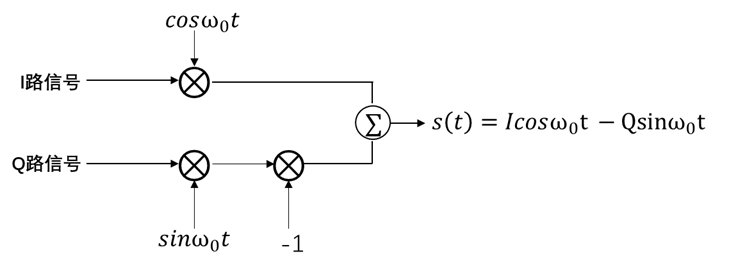
BPSK (Binary Phase Shift Keying) —— 二进制相移键控。
它的调制过程很简单，我们只使用一种载波： $cos(ω_0t)$
当输入的二进制信号是0时， $s(t) = cos(ω_0t)$；当输入的二进制信号是1时， $s(t) = cos(ω_0t + Π)$

而我们知道： $cos(ω_0t + Π) = -cos(ω_0t)$，那么我们可以得到下面的映射关系：

输入的二进制信号	对应的I、Q信号	调制后的波形
0	I = 1；Q = 0	$s(t) = cos(ω_0t)$
1	I = -1；Q = 0	$s(t) = cos(ω_0t + Π)$

1.1 用旋转向量的角度理解BPSK调制

首先，我们先明确一个概念：正频率 $f = 2Πω$表示旋转向量沿逆时针旋转；复频率 $-f = -2Πω$表示旋转向量沿着顺时针旋转。（这个概念的分析我们将在后续博文中学习）

那么，由于BPSK中，输入0时，输出 $s(t) = cosω_0t$，输入1时，输出 $s(t) = cos(ω_0t + Π)$。

那么，如果在旋转向量的角度上，输入0，输出 $s(t) = cosω_0t$的情况相当于初始位置如下图（a）所示的逆时针旋转向量在实轴上的投影；输出1，输出 $-cosω_0t = cos(ω_0t$ + Π)$的情况相当于初始位置下图（b）中顺时针旋转的向量在实轴上的投影

请注意：上图展示的分别是传输为0和1时初始位置的向量，我们知道，对于BPSK，传输每一个二进制信号之间都是会有时间间隔的，那么它们在这个时间间隔中是会一直旋转的！那么调制的过程，就是这个旋转向量在旋转过程中在实轴上的映射（这个在实轴上的映射波形就是调制波形）

可能大家不太能够想象旋转向量旋转时在实轴上的映射是怎么样的波形，那么下面通过一个动图看看单位向量： $e^{jω_0t}$（频率为+，代表逆时针旋转）旋转过程中在实轴上的映射波形和在虚轴上的映射波形：

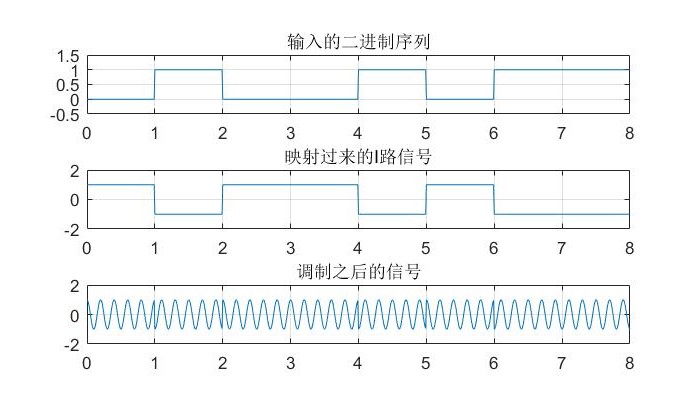
1.2 用Matlab实现BPSK调制过程

我们打算传输的一段二进制序列是“ 0 1 0 0 1 0 1 1”，使用的载波频率是 $f_c$ = 5

subplot(4,1,1);      %第一个图
t = 0:0.01:8;
d = [0 0;0.5 0;1 1;1.5 1;2 0;2.5 0;3 0;3.5 0;4 1;4.5 1;5 0;5.5 0;6 1;6.5 1;7 1;7.5 1;8 1];
signal = pulstran(t - 0.25, d, 'rectpuls', 0.5);   %矩形脉冲
plot(t, signal);
axis([0 8 -0.5 1.5]);
title('输入的二进制序列');
grid();

subplot(4,1,2);
d1 = [0 1;0.5 1;1 -1;1.5 -1;2 1;2.5 1;3 1;3.5 1;4 -1;4.5 -1;5 1;5.5 1;6 -1;6.5 -1;7 -1;7.5 -1;8 -1];
I = pulstran(t-0.25, d1, 'rectpuls', 0.5);
plot(t, I);
axis([0 8 -2 2]);
title('映射过来的I路信号');
grid();

subplot(4,1,3);
d3 = [0 0;0.5 0;1 0;1.5 0;2 0;2.5 0;3 0;3.5 0;4 0;4.5 0;5 0;5.5 0;6 0;6.5 0;7 0;7.5 0;8 0];
Q = pulstran(t-0.25, d3, 'rectpuls', 0.5);
plot(t, Q);
axis([0 8 -2 2]);
title('映射过来的Q路信号');
grid();

s1 = I.*cos(2*pi*5*t);
s2 = Q.*sin(2*pi*5*t);
output = s1 - s2;
plot(t, output);
axis([0 8 -2 2]);
title('调制之后的信号');
grid();

二、BPSK解调过程

2.1 用旋转向量的角度理解BPSK解调

通过上文的学习我们知道，如果我们接受的是一个旋转向量，并且假设接收端接收到0时刻和t时刻的旋转向量如图所示：

为了解调出信号0或者1，我们可以给接受的旋转向量乘上顺时针旋转的单位向量： $e^{-jω_0t}$

那么，我们就可以得到一个静止的向量，他不会乱跑，因此我们可以很轻松地知道传输过来的是什么数字。但是，理想很美好，现实很骨骨感 —— 我们实际上传输的，是旋转向量在实轴上的投影，那么，我们应该怎么办呢？

还记得么，BPSK传输0时的 $s(t) = cos(ω_0t)$，传输1时的 $s(t) = -cos(ω_0t)$
别忘了我们还有这个利器： $cosω_0t = \frac{1}{2}(e^{jω_0t} + e^{-jω_0t})$

上面这样做，就可以理解为把 $cosω_0t$分解为了两个幅值为 $\frac{1}{2}$，一个逆时针旋转；一个顺时针旋转的向量，如下图所示：

那么，现在的解调，第一步，我们可以这样做：把 $s(t)$乘上顺时针旋转单位向量 $e^{-jω_0t}$，再乘2。这样，我们就可以得到一个静止的，模为1的向量和一个顺时针旋转，角速度为 $2ω_0$的向量

$\begin{aligned} 2e^{-jω_0t}cos(ω_0t) &= 2e^{-jω_0t}\frac{1}{2}(e^{jω_0t} + e^{-jω_0t})\\ &=1 + e^{-2jω_0t}\\ \end{aligned}$
取出其中那个不旋转的向量，我们就可以解调出需要的信号了。对于 $s(t) = -cos(ω_0t)$的情况也是一样的处理。
$\begin{aligned} -2e^{-jω_0t}cos(ω_0t) &= -2e^{-jω_0t}\frac{1}{2}(e^{jω_0t} + e^{-jω_0t})\\ &=-1 + e^{-2jω_0t}\\ \end{aligned}$
按这样的方法，输入0时解调得到的是 $1 + e^{-2jω_0t}$；输入1时得到的是 $-1 + e^{-2jω_0t}$

我们看到：向量 $1 + e^{-2jω_0t}$包括一个静止分量1，和一个角频率为 $-2ω_0$，顺时针方向旋转的向量。
$-1 + e^{-2jω_0t}$包括一个静止分量-1，和一个角频率为 $-2ω_0$，顺时针方向旋转的向量。

那么，取出那个不旋转的向量就可以解调出+1 和 -1 ，从而得到输入信号是0还是1

【问题来了】：如何取出那个不旋转的向量+1和-1呢？

1. 使用低通滤波器，滤去高频分量，得到直流量。
2. 通过积分。

下面我们看看用积分怎么取出直流量：
【1】当我们接收到的信号是 $s(t) = cos(ω_0t)$时，我们做如下的积分：
$\begin{aligned} &\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}2s(t)e^{-jω_0t}dt \\ &=\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}(e^{jω_0t} + e^{-jω_0t})e^{-jω_0t}dt \\ &=1 + \frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}e^{-2jω_0t}dt\\ &=1 + \frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}[cos(-2ω_0t) + jsin(-2ω_0t)]dt\\ &=1 \end{aligned}$
在上面的积分中，我们用了 $\int_{-\frac{T}{2}}^{\frac{T}{2}}costdt=0\quad \int_{-\frac{T}{2}}^{\frac{T}{2}}sintdt=0$

好啦，以上就是BPSK调制和解调的数学过程，并使用IQ调制实现，下面我们综合来看看整个过程：

四、利用复数运算实现BPSK调制

我们还记得用复数运算实现IQ调制的过程：

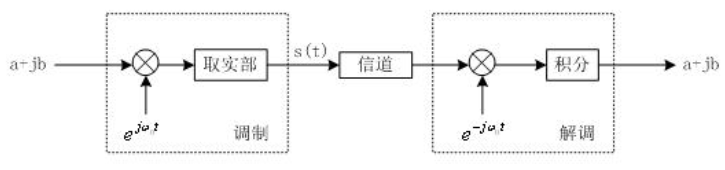
【特别要记得还有“取实部”这一过程！】
我们上文提到了BPSK调制过程中，输入信号和I,Q信号的映射关系里面，始终有Q = 0，即：b = 0。
那么用复数运算实现BPSK调制，我们需要将上图中的b = 0：

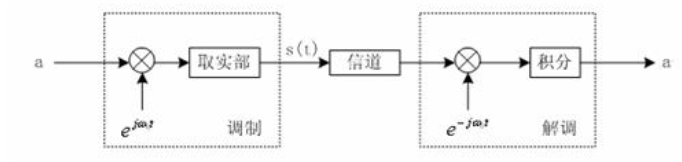
那么，我们发送出去的调制信号 $s(t)$就等于 $Re(ae^{jω_0t}) = acos(ω_0t)$
Tips：在我们用matlab仿真BPSK调制的时候，我们的调制信号也是直接写成 $s(t) = acos(ω_0t)$了

%%%举个例子(伪代码）%%%
fc %载波频率
fs %采样频率
假设定义好了t和 I 路信号
那么, s(t) = I.*cos(2*pi*fc*(t/fs));   %相当于上图中的取实部了

五、利用实数运算实现BPSK调制

其实，调制过程和就是我们伪代码的思路，解调过程是将接收到的信号再乘上一样的 $cos(ω_0t)$，再积分，我们看看框图：

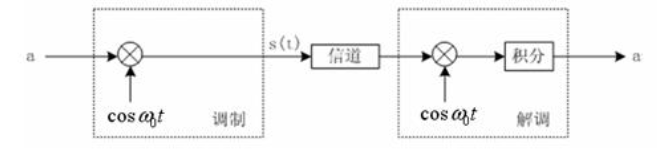
我们用数学方法看看用实数运算实现BPSK解调的过程：(以当接收到的信号是 $cos(ω_0t)$为例）
$\begin{aligned} &\frac{2}{T}\int_{-\frac{T}{2}}^{+\frac{T}{2}}cos(ω_0t)cos(ω_0t)dt\\ &=\frac{2}{T}\int_{-\frac{T}{2}}^{+\frac{T}{2}}cos^2(ω_0t)dt\\ &=\frac{2}{T}\int_{-\frac{T}{2}}^{+\frac{T}{2}}(\frac{1}{2} + \frac{1}{2}cos(2ω_0t))dt\\ &=1 \end{aligned}$