【通信原理 入坑之路】 —— 详细理解傅里叶变换以及它在通信里面的应用

一，实傅里叶级数和复傅里叶级数

1.1实傅里叶级数

我们还记得高数中实傅里叶级数的公式吗？ $f(t) = \frac{a_0}{2} + \sum_{k=1}^{∞}(a_kcoskω_0t + b_ksinkω_0t)$
它表示了任何一个函数都可以化成无穷多个幅度、频率不同的正弦波的叠加

为了直观感受傅里叶变换的魅力，我们试着用正弦波近似表示方波：
首先，我们画一个简单的：y = 0.5 + 0.637.*cos(x);

x = 0:0.01:30;
y = 0.5 + 0.637.*cos(x);
plot(x, y)

再来看看 y=0.5+0.637.*cos(x)-0.212.cos(3x); 叠加了另外一个正弦波：

x = 0:0.01:30;
y=0.5+0.637.*cos(x)-0.212.*cos(3*x);
plot(x, y)

如果我们试着再叠加正弦波呢？y=0.5+0.637.*cos(x)-0.212.cos(3x)+0.127.cos(5x);

x = 0:0.01:30;
y=0.5+0.637.*cos(x)-0.212.*cos(3*x)+0.127.*cos(5*x);
plot(x, y)

我们能看到：如果叠加无穷多个正弦波，那么最终就会无限趋近于方波了

通过实傅里叶变换公式： $f(t) = \frac{a_0}{2} + \sum_{k=1}^{∞}(a_kcoskω_0t + b_ksinkω_0t)$
我们可以直接看出一些简单函数的傅里叶系数a，b
例如， $y = sint$中， $a_0 = 0, a_1 = 0, b_1 = 1$
$y = cost$中， $a_0 = 0, a_1 = 1, b_1 = 0$
【当然， $a_0, a_k, b_k$有特定的公式可以计算，这里不打出来了】

1.2 复傅里叶级数

首先，由复变函数的知识我们知道： $sinω_0t = \frac{1}{2j}(e^{jω_0t} - e^{-jω_0t}) = -\frac{j}{2}(e^{jω_0t} - e^{-jω_0t})$
$cosω_0t = \frac{1}{2}(e^{jω_0t} + e^{-jω_0t})$
我们把这两个式子带入上面的实傅里叶级数公式：
$\begin{aligned} f(t) &= \frac{a_0}{2} + \sum_{k=1}^{∞}(a_kcoskω_0t + b_ksinkω_0t)\\ &=\frac{a_0}{2} + \frac{1}{2}\sum_{k=1}^{∞}[(a_ke^{jkω_0t} + a_ke^{-jkω_0t})-j(b_ke^{jkω_0t}-b_ke^{-jkω_0t})]\\ &=\frac{a_0}{2} + \frac{1}{2}\sum_{k=1}^{∞}(a_k - jb_k)e^{jkω_0t} + \frac{1}{2}\sum_{k=1}^{∞}(a_k + jb_k)e^{-jkω_0t}\\ &=\sum_{k=0}\frac{a_k}{2} +\frac{1}{2}\sum_{k=1}^{∞}(a_k - jb_k)e^{jkω_0t} + \frac{1}{2}\sum_{k=-1}^{-∞}(a_{-k} + jb_{-k})e^{jkω_0t}\\ &=\sum_{k = -∞}^{+∞}c_ke^{jkω_0t} \end{aligned}$
对于复傅里叶系数 $c_k$，有： $c_k = \begin{cases} \frac{a_0}{2} \quad k = 0\\ \frac{1}{2}(a_k - jb_k) \quad k = 1,2,...\\ \frac{1}{2}(a_{-k} + jb_{-k}) \quad k = -1,-2,...\\ \end{cases}$
那么，只要我们就出了 $a_k, b_k$，就可以把复傅里叶系数 $c_k$计算出来。

二，频谱与卷积

上面的一大堆公式推导都是为这一节做了铺垫。首先，什么是频谱呢？
我们生活中就有一个很恰当的例子：

我们平常听的音乐，如果在时域中，是一个振幅随时间变化的波形，像下图这样：

而音乐的另外一种表达，则是大家更为熟悉的——音符

这种用音符表示音乐的方法，我们可以认为是频域的表示。
例如，使用傅立叶变换，诸如人类语音的声波可以被分解成其不同频率的音调分量，每个音调分量由具有不同幅度和相位的正弦波表示

2.1 频谱

频谱是频率谱密度的简称，是频率的分布曲线。复杂振荡分解为振幅不同和频率不同的谐振荡，这些谐振荡的幅值按频率排列的图形叫做频谱。
也就是说，频谱横坐标是频率，纵坐标是该频率下对应的幅度

还记得我们在上一篇文章里面表示的信号 $f(t), g(t)$吗？
【通信原理 入坑之路】——深入、详细地理解通信里面“卷积”概念

$f(t) = e^{j2ω_0t} + 5e^{jω_0t} + 6$； $g(t) = 3e^{jω_0t} + 2$
上面这个是 $f(t), g(t)$两个信号的时域表示，下面我们画出它的频谱
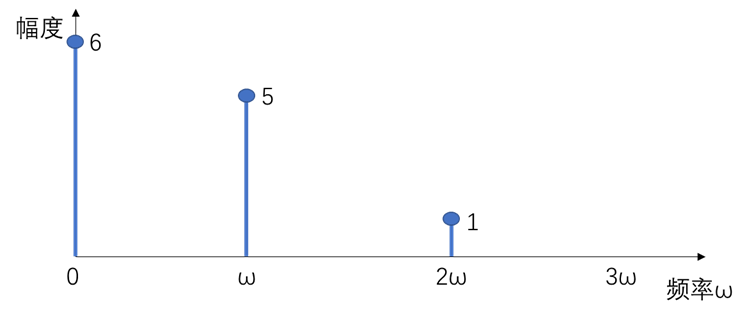
先画 $f(t)$的，我们看到 $f(t)$信号可以分解为频率为0， ω_0，2ω_0三种频率的信号的叠加
频率为0的信号幅度为6；频率为 $ω_0$的信号幅度为5；频率为 $2ω_0$的信号为1

下面是 $g(t)$的频谱

因此，[1 5 6]*[3 2] = [3 17 28 12]。我们平常所说的频域，实际上指的是频谱，也就是 $e^{jkω_0t}$前面的系数。那么，做信号时域上的乘法就可以等效成信号频域的卷积，再乘上对应的 $e^{jkω_0t}$

上图中最左边的黑色曲线是由右边各种彩色的，幅度不同、频率不同的正弦波组成的。那么，从图中黑色箭头方向看进去，就是组成黑色波形的各种频率成分的正弦波对应的幅度值，也就是频域图像

补充：时域卷积定理

上文我们提到了：“做信号时域上的乘法就可以等效成信号频域的卷积，再乘上对应的 $e^{jkω_0t}$

那么，信号在时域上的卷积会等于信号的频域相乘！

三、用两个生动的例子阐释傅里叶变换的作用

【例子一】：现在一家餐厅研究了一个特殊的美食，作为美食家的你，想知道这个菜里面到底都有什么配料。那么，如果我们输入这个美食（这个美食就是我们的“时域信号”），通过傅里叶变换，就可以得到这份美食的配方（这个配方就是我们的“频域信号”）

如果我们输入的是这个美食的配方，就可以通过傅里叶反变换得到这份美食

【例子二】：下面请读者和我一起做一件事情：我将给出 $sin(3x) + sin(5x)$的曲线（你只知道这个曲线的样子，并不知道这个曲线的方程），那么应该如何去掉 $sin(5x)$的成分呢？
想在时域中完成这个简直难于上青天，可以在频域中却很简单。

四、傅里叶变换与调制解调的关系

我们知道，IQ调制中，调制信号 $s(t)$可以表示为： $s(t) = acosω_0t - bsinω_0t$
关于IQ调制的具体知识可以参考：【通信原理 入坑之路】—— 星座图原理分析与IQ调制

而我们又知道，傅里叶变换公式是： $f(t) = \frac{a_0}{2} + \sum_{k=1}^{∞}(a_kcoskω_0t + b_ksinkω_0t)$
当k = 1（只有基波分量的时候）且 $a_0 = 0$， $a_k = a，b_k = -b$时， $f(t) = s(t)$

因此，调制的过程就是用傅里叶系数和正余弦信号相乘，产生一个新的信号发送的过程。
解调就是求解傅里叶系数的过程
即信号的调制解调是傅里叶变换的一个简单的应用！

4.1 用复傅里叶级数实现IQ解调的原理

我们回顾一下IQ调制中使用复数进行解调的过程：

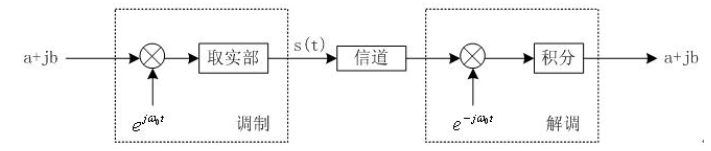
这里我们对经过信道的 $s(t)$先乘上了一个顺时针旋转的单位向量 $e^{-jω_0t}$，再进行积分就可以解调出I, Q信号。可是，他和复傅里叶变换有啥关系呢？

在上文中，我们知道了复傅里叶系数 $c_k$的计算公式：
$c_k = \begin{cases} \frac{a_0}{2} \quad k = 0\\ \frac{1}{2}(a_k - jb_k) \quad k = 1,2,...\\ \frac{1}{2}(a_{-k} + jb_{-k}) \quad k = -1,-2,...\\ \end{cases}$
而对于傅里叶变换在解调中的应用，我们取基波（k = 1），且 $a_0 = 0$
因此，对于上图IQ解调的过程， $c_k = \begin{cases} \frac{1}{2}(a_1 - jb_1) \quad k = 1\\ \end{cases}$
我们只需要求解出 $a_1, b_1$即可。

由于： $\begin{aligned} s(t) &= acos(ω_0t) - bsin(ω_0t) \\ &= \frac{a}{2}(e^{jω_0t} + e^{-jω_0t}) +\frac{jb}{2}(e^{jω_0t} - e^{-jω_0t})\\ &=(\frac{a}{2} + \frac{jb}{2})e^{jω_0t} + (\frac{a}{2} - \frac{jb}{2})e^{-jω_0t} \end{aligned}$

由复傅里叶系变换： $f(t) =\sum_{k = -∞}^{+∞}c_ke^{jkω_0t}$
我们可以知道： $c_1 = \frac{a}{2} + \frac{jb}{2}；c_{-1} = \frac{a}{2} - \frac{jb}{2}$
那么，只要我们求出了 $c_1$，我们就可以解调出a, b

4.1 如何求解复傅里叶系数?

回顾一下复傅里叶系数： $f(t) = \sum_{k = -∞}^{+∞}c_ke^{jkωt}$
我们知道， $e^{jkωt}$可以表示为不同角速度的旋转向量，因此，我们可以把 $f(t)$分解为若干个不同角速度，不同旋转方向的旋转向量（当k > 0时逆时针旋转，k < 0 时顺时针旋转）

那么，对于组成 $f(t)$的某一个旋转向量 $e^{jmω_0t}$而言，乘上一个 $e^{-jmω_0t}$，那么它就变成了一个静止的向量，就可以得到地第m项的复傅里叶系数！但是，其他向量和这个 $e^{-jmω_0t}$相乘依然还是会旋转，不过这并不影响！我们通过数学方式来看看：
$\begin{aligned} &\frac{1}{T}\int_{-\frac{T}{2}}^{+\frac{T}{2}}f(t)e^{-jmω_0t}\\ &=\frac{1}{T}\int_{-\frac{T}{2}}^{+\frac{T}{2}}\sum_{k = -∞}^{+∞}c_ke^{jkωt}e^{-jmω_0t}\\ &=\frac{1}{T}\int_{-\frac{T}{2}}^{+\frac{T}{2}}c_m + \frac{1}{T}\int_{-\frac{T}{2}}^{+\frac{T}{2}}\sum_{k = -∞;k≠m}^{+∞}c_ke^{jkωt}e^{-jmω_0t}\\ &=c_m \end{aligned}$
我们刚刚的推导得出了任意一项复傅里叶系数 $c_m$的计算公式： $c_m = \frac{1}{T}\int_{-\frac{T}{2}}^{+\frac{T}{2}}f(t)e^{-jmω_0t}$

还记得上一节我们说：只要就出了 $c_1$既可以得到a 和b嘛。因此：
$c_1 = \frac{1}{T}\int_{-\frac{T}{2}}^{+\frac{T}{2}}f(t)e^{-jω_0t}$

但是由于 $c_1 = \frac{a}{2} + \frac{jb}{2}$，我们还要对 $c_1$乘以一个2，才能真正得到a, b
即： $a+jb = \frac{2}{T}\int_{-\frac{T}{2}}^{+\frac{T}{2}}f(t)e^{-jω_0t}$

4.2 傅里叶级数与正交频分复用OFDM的关系

一图胜千言：

OFDM调制的过程，就是把输入的 $a_1, b_1, a_2, b_2 、、$作为傅里叶系数和 $cos(ω_0t), sin(ω_0t), cos(2ω_0t), sin(2ω_0t),、、$相乘的过程。

OFDM解调的过程就是把 $s(t)$做傅里叶级数展开，求解傅里叶系数的过程！

这里再附上求解傅里叶级数的计算公式： $a_k = \frac{2}{T}\int_{-\frac{T}{2}}^{+\frac{T}{2}}f(t)cos(kω_0t)dt \space (k=0,1,2..)\\ \quad\\ b_k = \frac{2}{T}\int_{-\frac{T}{2}}^{+\frac{T}{2}}f(t)sin(kω_0t)dt\space (t=1,2,...)$