【通信原理 入坑之路】—— 信号的包络分析2 包络分析的意义以及OQPSK调制的引入

本篇 $Blog$ 是接上一篇未完的分析而作的，主要是继续深入理解信号包络以及包络的意义。同时，本篇 $Blog$ 是《深入浅出通信原理》的学习笔记，仅供个人学习记录使用

一、信号包络产生的回顾

还记得我们之前学习到的信号包络吗？我们先简单回顾一下它的产生：
首先是 $I, Q$ 信号波形的产生：

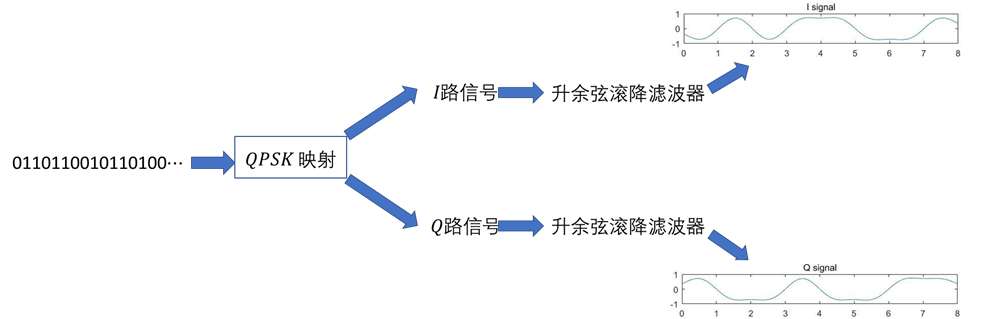
接下来是和调制载波相乘：（实数运算实现）

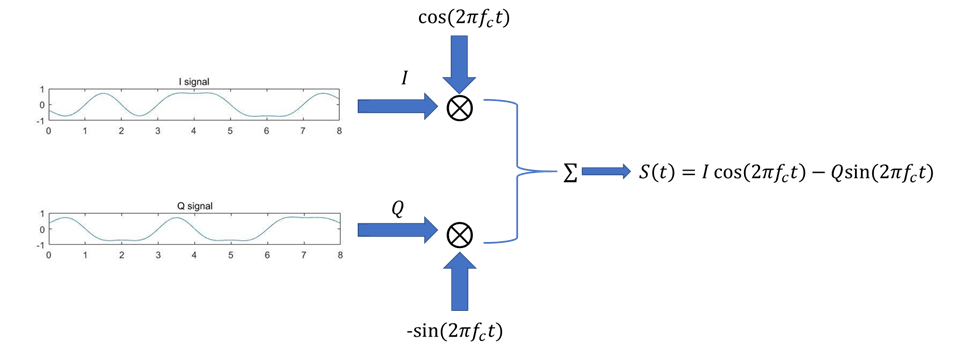
然后，我们说更常用的，是使用复数运算实现：

因为，我们知道 $e^{2Πf_ct}$ 随时间变换的三维立体图是一个螺旋前进的单位旋转向量。

而由于现在经过了升余弦滚降滤波器，因此 $I, Q$ 信号就变成了随时间变化的函数，另外大家注意一点就是我们实际上传播的是实信号，而不是复信号。也就是说，我们看到上图取实部得到 $s(t)$ 的第二个表达式，就是一个余弦载波，其相位和幅度都随时间变化，因此，我们得到实际上传输的高频信号的波形就是：

而通过 $s(t)$ 的第二个表达式我们也知道了，这个高频信号 $s(t)$ 的幅值就是 $\sqrt{I(t)^2 + Q(t)^2}$
对应着的 $\sqrt{I(t)^2 + Q(t)^2}$ 和 - $\sqrt{I(t)^2 + Q(t)^2}$ 的波形就是这个高频信号的包络

二、包络的严格定义

我们之前的博文中，在学习到 IQ 调制的时候，我们使用了旋转向量的角度理解 IQ 调制：

还记得我们在没有引入升余弦滚降滤波器的时候，映射出来的 $I, Q$ 信号在一个码元的持续时间里面都是一个常数，要么是 $+\frac{1}{\sqrt{2}}$，要么是 $-\frac{1}{\sqrt{2}}$，固然，这样的 IQ 调制得到的信号（ $Re[(I+jQ)e^{j2Πf_ct}]$ 的幅度就等于1，是一个常数。

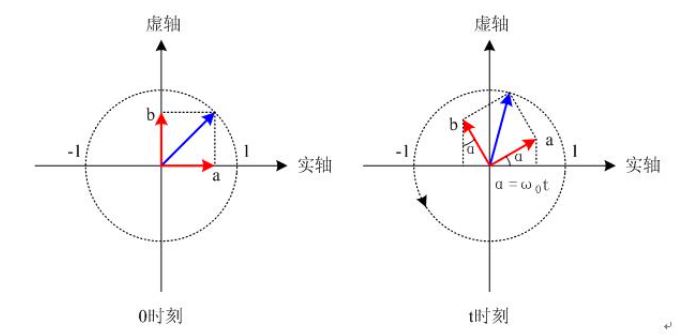
因此，由上图所示，此时的 IQ 调制得到的信号就是一个幅度为1 ，频率为 $f_c$（旋转角速度为 $ω_c$ 的旋转向量。

而现在，我们引入了升余弦滚降滤波器之后， $I, Q$ 信号都是随时间变化的向量，那么自然地，它们合成的 $s(t)$，也是幅度和相位随时间变化的旋转向量了

那么严格地讲，这个 $s(t)$ 旋转向量的模长： $\sqrt{I(t)^2 + Q(t)^2}$ 才是真正包络的严格定义。

不变的是，我们实际传输的信号，依旧是这个旋转向量 $s(t)$ 在实轴上的投影。

因此，上述的包络应该画成：

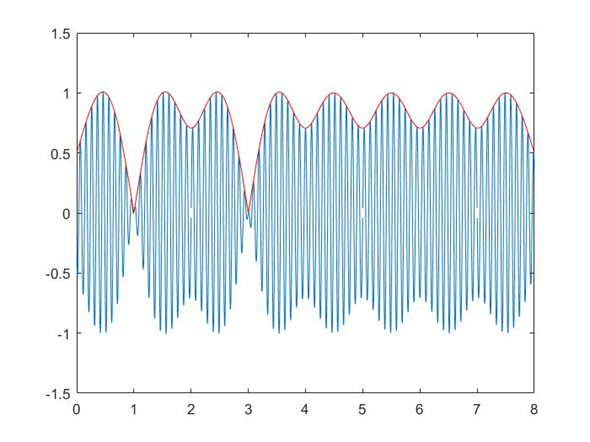
三、从三维空间的角度看包络

如果我们试着把上面我们讲到的 $s(t)$ 旋转向量向量末端的轨迹画出来，会是什么样子的呢？

如果我们在这个基础上，把包络线的三维空间图也画出来（为什么包络线有三维空间的图呢？因为包络线的定义： $\sqrt{I(t)^2+Q(t)^2}$，那么它在三维空间中就应该可以表示为： $I + jQ$）

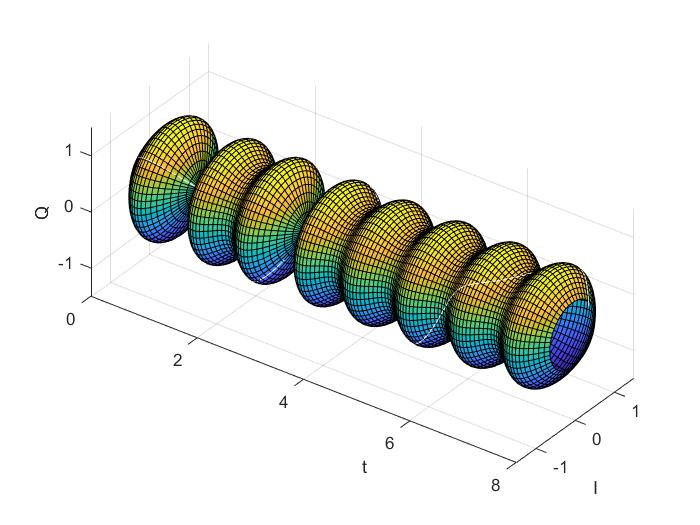
大家能看到白色的那条包络线吗？它在空间中就长这样。
下面我们把三维空间中的包络线单独拿出来从不同的角度看看，看看有什么特点：

我们看到这个空间中的线，在 $I-t$ 平面的投影和我们之前画的 $I$ 路信号一模一样。
在 $Q-t$ 平面上的投影和之前画的 $Q$ 路信号一模一样。

这只是最表层的一点点特点，我们再深入挖掘一下：
首先，我们还记得这个波形所代表的，我们要传输的二进制序列吗？ $0110110010110100$

每一个码元持续的时间是 $1$ 秒，那么我们就以码元持续时间的中间时刻代表代码元（这是什么意思呢？因为我们在接收端解调之后不是要抽样判决吗？我们抽样的时刻就是 $kT_s$ 对吧，在上述情况下就是每隔 1 秒，抽一个样，那么很明显，我们抽样的位置肯定要在这个码元持续时间的中间抽，这样才会准确嘛）

所以，最后抽样得到的码元，都是抽样在码元持续时间中间时刻的码元

所以，下面我们再看看这个空间包络图：

蓝色箭头代表的是随着时间的推进，空间包络线的走向。

3.1 从包络理解星座图的由来

下面，我们就看看在每一个码元持续时间的中间时刻，那个对应的码元在那个位置：

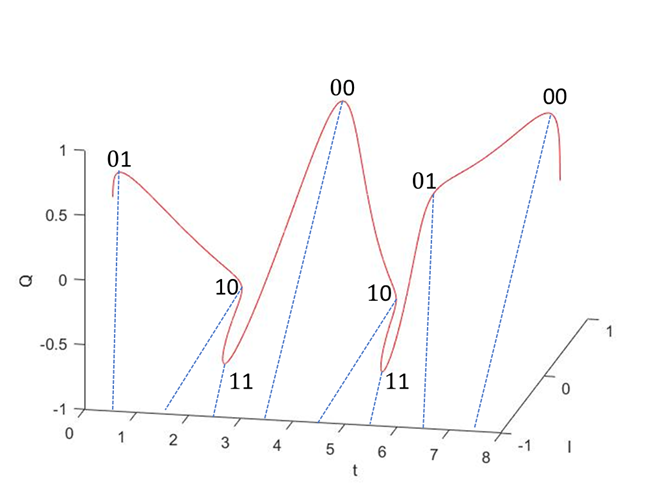
现在，我们已经清楚空间包络线不同时刻对应的码元了。但是这还不够，因为我们还记得星座图嘛？它是码元在 $I-Q$ 平面上的分布图。对应地，也就是我们上面这个空间包络图从右往左看进去，不同码元的分布情况。因此我们来看看：

因此，下图就是QPSK 调制的星座图了。至此，想必大家应该对星座图的由来有了一个新的认识了！

3.2 信号包络分析的意义

先贴上我们要传输的数据： $0110110010110100$
结合着空间包络走势图和上面这张星座点的映射图，我们分析一下：

当传输第一个码元 01 时，星座点位于上图的左上角，紧接着传输第二个码元 10，那么包络线就会沿着对角走到右下角：在这个过程中，我们发现 $I$ 信号和 $Q$ 信号的幅值都是逐渐减小到0， 再从0 慢慢增大回去，当包络经过正方形的中心点的时候，对应的实包络就会等于0.

对应关系如下图所示：

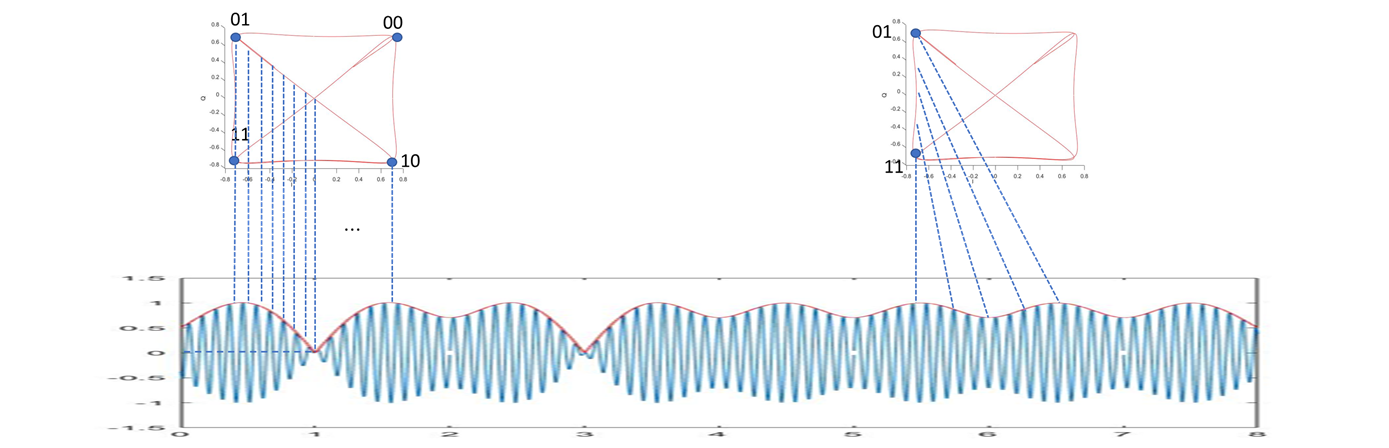
也就是说：如果我们传输的正方形边上的两个码元，那么实包络线的幅度就变化不会很大，而且不会变成0. 而如果我们传输的两个码元是处于正方形的对角，那么实包络线就一定会先变成0，这样的话，实包络线的幅度变化就会比较大了。

讲了这么多，问题的关键是：我们为什么要分析包络？？

因为在实际中，我们经过了调制之后的信号，因为比较微弱，还需要经过功放（功率放大器）的放大才发射出去。如下图所示：

为了使得信号在经过放大之后不失真，我们需要使用线性功放。可是，这有遇到一个问题：使用线性功放的话，成本太高。那么，如果使用成本较低的非线性功放呢？

既然是非线性功放，势必会造成失真。不过我们在抽样判决的时候是有一个判决范围的，也就是属于一个范围内的，都可以被判决为某一个符号。因为，为了尽可能的减小失真造成的误判，我们就希望这个待放大的信号变化的程度小一点，尽可能平稳一些，这样才不至于出现特别大的失真。

四、OQPSK调制的引入

准备条件

1. 上文中，我们讲，希望这个待放大的信号变化的程度小一点，尽可能平稳一些，这样才不至于出现特别大的失真。也就是说，我们希望这个待放大的信号的包络变化的小一点

2. 我们在包络分析中还知道了一个特点：如果我们传输的正方形边上的两个码元，那么实包络线的幅度就变化不会很大，而且不会变成0. 而如果我们传输的两个码元是处于正方形的对角，那么实包络线就一定会先变成0，这样的话，实包络线的幅度变化就会比较大了

结合上面的要求和特点：我们想：如果我们每次传输的都是正方形边上相邻的两个码元是不是就能避免这种情况了！

这就是 OQPSK 调制的由来！

今天的 $Blog$ 就暂时写到这儿，我们进一步深入分析了信号包络，并且有包络分析引出了 QPSK调制的改良版——OQPSK。在下一篇 $Blog$ ，我们就一起学习 OQPSK 调制的细节！