【通信原理 入坑之路】—— 深入理解奈奎斯特第一准则与码间串扰

写在前面：本博客是《深入浅出通信原理》的学习笔记，仅供个人学习记录使用

一、从宏观上看奈奎斯特第一准则的应用

一个通信系统模型大致如下图所示：

我们今天学习到的奈奎斯特第一准则，就是应用在 “映射，脉冲称性” 模块和 “抽样判决” 模块。

下面简单解释一下模块的工作内容：还记得之前的 $Blog$ 里面关于 “采样” 的应用嘛？它属于 “信源编码” 的模块，一个模拟信号，经过采样，保持，量化，编码之后，就变成了像 “0010110101 $\cdots$” 这样的二进制信号，“信道编码” 和 “交织” 模块暂时还没有写到，不过没有关系，我们现在先这样理解，经过 “信道编码” 和 “交织” 这两个模块之后，我们得到的还是二进制的单位冲击序列。

然后，我们根据需要把这些二进制序列按照 $k$ 个比特这样划分成一组（比如说，如果我们以 2 个比特为一组，就可以把上面的二进制序列划分成 00、10、11、01、01、 $\cdots$，我们把这样 $k$ 个二进制序列的小组，称为一个码元，我们要对这些码元进行脉冲成型，也就是再变回到连续的模拟信号，然后调制成高频信号 ，经过天线发射。

在接收端，我们解调之后，就恢复成了低频的连续模拟信号，我们以 $T_s$ 的采样时间间隔对这个模拟信号采样，根据采样的值，来判断它是哪一个码元。那么，如果我们在某一个抽样时刻 $t_0$ 抽样得到的模拟信号的值不幸收到了其他码元的干扰，那么我们就称这叫做产生了 “码间串扰”。

而奈奎斯特第一准则，就是针对码间串扰问题的

二、奈奎斯特第一准则的相关细节

2.1 表述

先看看 奈奎斯特第一准则 的表述：在带宽为 B 的信道上传送码元时，要想实现无码间串扰，码元速率 $R_s$ 不能超过 2 倍的带宽。即： $R_s ≤ 2B$，要达到最高传输速率（奈奎斯特速率） 2B， 必须使用带宽为 B 的理想低通滤波器进行滤波。

2.2 码元的传输和码间串扰

我们以一个二进制序列 $00010110$ 为例：

我们现在所处的，是通信系统模型的第四个框框：映射+脉冲成型。

下面我们规定映射：0 $\rightarrow$ +1；1 $\rightarrow$ -1
那么下面到了脉冲成型，我们第一反应是成型成那种 双极性矩形波。生成理想的矩形波，需要使用矩形脉冲信号。 但是，矩形脉冲信号的带宽 B 无限大，而信道的带宽是有限的，一个无限带宽的信号经过一个带宽有限的信道，必然发生信号失真。

为了让信号不发生失真，我们现在试着使用一下 $sinc$ 脉冲信号
下图展示的是带宽为 2B 的 $sinc$ 脉冲信号。

它的傅里叶变换，也就是 $h(t) = sinc(t)$ 的频率响应大家应该不陌生。

下面，我们就来看看什么样才算是没有码间串扰：
我们先画出刚刚那个二进制序列：

figure(1);
n=0:1:7;
y=[1,1,1,-1,1,-1,-1,1];
stem(n,y) ;
axis([ -1 8 -1.5 1.5]); 
%此时，y里面的每一项都是一个码元，码元时间间隔是Ts，码元速率Rs

下面，我们需要对这个冲击序列做脉冲成型，使用 $sinc$ 脉冲函数。
那么，情况一：我们现在使用的是 $h(t) = sinc(t)$ 的脉冲函数，它的带宽为： $B = 0.5$ 假设我们现在以最高传输速率 $R_s = 2B = 1$ 来传输码元，也即是 $T_s = 1$。OK，在各项参数都说明完了之后，我们就让这个冲击序列输入脉冲成型滤波器：

下图是把每一个单独的冲击序列输入脉冲成型滤波器的输出响应都画在了一起：

因为是线性时不变系统，我们在《信号与系统》中也有类似的例子，把每一个单位冲激响应加权叠加，就是信号输入这个系统得到的输出。因此，这些红色的，代表加权之后的脉冲响应的叠加如下图所示：

如果我们只关注冲击序列经过脉冲成型滤波器的输出结果，那么如下图所示：

这个就是最终的输出结果，我们到时候就会拿它进行调制。

在抽样判决端，我们也是以 $T_s$ 的抽样周期进行抽样判决，过程如下图：

我们看到，每一个时刻抽样得到的值都非常准确地反映到相应的映射值，比如在抽样时刻 $1T_s$ 处就等于 1 ，抽样时刻 $6T_s$ 处就等于 -1 等等。

至此，我们已经熟悉了通信系统中是如何进行脉冲成型和抽样判决的了，可是，似乎并没有看出这个码间串扰问题和最大码元速率的关系呀？别急，好戏现在才开始上演：

首先，我们来分析上面这样传输中抽样判决的过程：我们知道，那个绿色的线就是上图中所有红色线的叠加，对吧，那么也就是说，在某一个抽样时间 $kT_s$ 内，我们对这个绿色线的抽样，抽样得到的值应该是上面所有红色线在这个时刻 $kT_s$ 处值的叠加。

而我们看看顺数第3幅图中，任何一个时刻 $kT_s$中，我们的冲激响应幅度都是当前该时刻的码元的值 +1 或者是 -1，其他码元的值都是0，也就是说，我们在抽样时刻 $kT_s$ 抽样得到的值就是该时刻的码元值 +1 或 -1，不掺杂其他码元的值。

这样，我们就说是：没有码间干扰！

现在，我们来看看另外一种情况：如果我们保持脉冲成型滤波器的带宽依然是 $B = 0.5$，即还是用： $h(t) = sinc(t)$ 的脉冲成型滤波器，但是我们将码元速率增大值： $R_s = 2$
现在已经不满足奈奎斯特第一定律了，那么我们看看会发生什么情况：

先来看看输入成型滤波器的单位冲击序列：

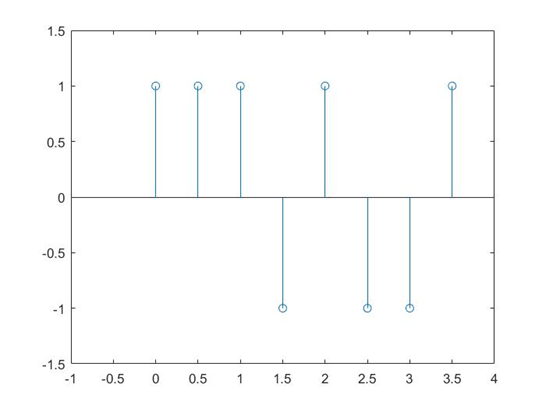
我们能够看到，现在 1 秒能够传输 2 个码元了。下面我们分解地画出每一个单位冲击信号输入脉冲成型滤波器的响应，用红色线标出：

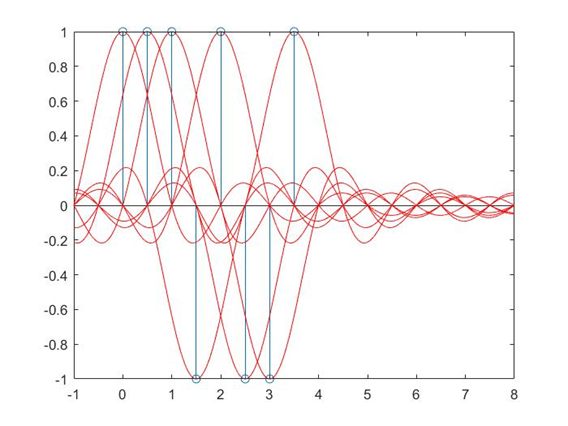
啊！混乱一片，我们可以看到，假如在抽样时刻 $kT_s$ 处，我们抽样得到的信号的幅值，必定不全是在 $kT_s$ 处的冲击响应的值了，而是结合了多个码元在这个时刻的响应的值了。我们把所有红色线叠加起来，看看输出的波形长什么样：

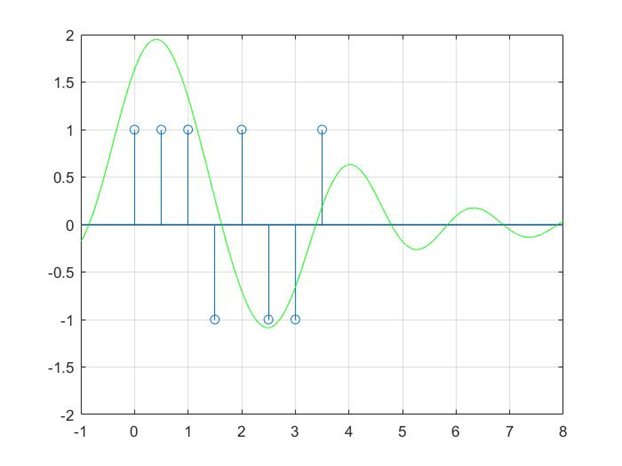
如果我们规定：抽样得到的值如果大于0，就把它判决为+1；抽样值如果小于0，就把它判决为-1。下面我们就来看看这个情况下判决得到的结果吧：

最终，我们判决得到的结果是： $+1, +1, +1, +1, -1, -1, -1, 1$，这和我们原本发送的消息序列有误，这就是码间串扰带来的问题了 —— 它会造成符号的误判。

2.3 码元的速率约束

从上面一大段的分析中，我们知道：如果码元速率 $R_s$ 不遵从奈奎斯特第一准则就会产生码间串扰，可以还记得我们对速率的要求嘛： $R_s ≤ 2B$

为什么呢？我们可以这样理解：要想不发生码间串扰，那么我们一个一个码元的冲击序列就必须放置在 $sinc$ 函数的零点处。

我们看到，图中，O, A, B, C, D, E, $\cdots$, 还有负半轴对称的那些点，都是 $sinc$ 函数的零点。而 $sinc$ 函数有一个性质，就是相邻的两个零点之间是等间隔的。

那么，现在回顾我们刚刚说过的话：“要想不发生码间串扰，那么我们一个一个码元的冲击序列就必须放置在 $sinc$ 函数的零点处。" 这是因为：只要你有一个码元的冲击序列放置在了 $sinc$ 函数的零点位置上，那么我们索要传输的所有码元就都会在 $sinc$ 函数的零点上了，这样就不会发生码间串扰！

既然我们现在知道了要把码元安放在 $sinc$ 函数的零点上，那么码元之间的间隔， $T_s$，也很容易取了。如果我们设 $sinc$ 函数两个相邻零点的距离是 $x$，那么 $T_s$ 可以等于 $x$, $2x$, $3x$, $\cdots$

结合一开始的关系： $x = \frac{1}{2B}$
那么，我们知道， $T_s$ 可以等于： $\frac{1}{2B}, \frac{1}{B}, \frac{3}{2B}, \cdots$
对应地，码元速率 $R_s$ 就可以等于： $2B, B, \frac{2B}{3}, \cdots$
因此，我们才说，最大码元速率就是 $2B$

但是工程上我们在不会发生码间串扰的前提下，不可能放着这个 $R_s = 2B$ 的速率不用而傻乎乎地跑去用更低的速度吧，因此，我们就说：如果我们选用的是理想低通滤波器（它的脉冲响应是 $sinc$ 函数），理想滤波器带宽是 B ，那么我们的码元速率 $R_s = 2B$ 的时候不会产生码间串扰。

至此，我们对奈奎斯特第一准则就比较了解了，但是问题还没有结束。

2.4 升余弦滚降滤波器

在实际的工作中，由于 $sinc$ 函数的小尾巴太长了，如果我们得不到精确的定时，很可能还是会出现码间串扰。因此，我们使用一种叫做 ”升余弦滚降滤波器” 的东西用作脉冲成型。

下面是升余弦滚降滤波器的频率响应： $H(f) = \begin{cases} \frac{1}{2B}, \space 0 ≤|f|<(1-α)B\\ \frac{1}{4B}[1+cos\frac{Π}{2Bα}[|f|-B(1-α)]], \space (1-α)B≤|f|<(1+α)B\\ 0, \space |f|≥(1+α)B \end{cases}$
单位冲激响应： $h(t) = \mathscr{F}^{-1}[H(f)] = sinc(2Bt)\frac{cos(2ΠαBt)}{1-(4αBt)^2}$

其中， $α$ 是升余弦滚降滤波器的重要参数——滚将系数

我们来直观地看看升余弦滚降滤波器在不同滚降系数下的单位冲击响应的图像：

我们可以看到：当滚降系数 $α$ 越大（1以内），冲激响应 $h(t)$ 的尾巴越短。

如果我们把 $α = 0, 1, 0.5$ 的 $sinc$ 函数，分别用红色、绿色、蓝色线画在一起：

最直观的感受是，这三个函数仿佛都经过（1，0）点！我们要想刚好不发生码间串扰，在码元速率最大的时候，我们就让相邻的两个码元之间的间隔为 1 就好了！也就是说： $R_s = 2B$

另外，随着滚降系数 $α$ 的不同，升余弦滚降滤波器的频率响应的带宽也有所不同：

1. 当 $α = 0$ 时，频谱宽度就是理想低通滤波器（频响为单位矩形脉冲）， $(1+α)B = B$
2. 当 $α = 0.5$ 时，频谱宽度 $(1+α)B = 1.5B$
3. 当 $α = 1$ 时，频谱宽度 $(1+α)B = 2B$