卡特兰数之不同的二叉搜索树

在前面写斐波那契数列的时候，突然想起来卡特兰数列，所以特地来重温一下。

什么是卡特兰数列

首先这里给出它的递推公式 C_n= C₀C_n-1+ C₁C_n-2+ ...+ C_n-1C₀

咋一看，看不明白，这就对了，咱来举几个例子：

这里我们先把第一项直接写出来 C₀= 1，那么

C₁ = C₀C₀ = 1 * 1 = 1

C₂ = C₀C₁ + C₁C₀ = 1 + 1 = 2

C₃ = C₀C₂ + C₁C₁ + C₂C₀ = 2 + 1 + 2 = 5

...

高中数学到此为止，再写得露馅，回到今天的例题。

不同的二叉搜索树

问题：给定一个整数 n，求以 1 ... n 为节点组成的二叉搜索树有多少种？

例：输入n = 3，则结果等于5。5种二叉搜索树如下：

分析：

这里我们注意一下二叉搜素树的性质，满足当前节点值大于左节点值，小于右节点值的二叉树才是二叉搜索树。

假设n个节点的二叉树搜索树的个数是G_n，以 i(1 <= i <= n) 为根节点的二叉搜索树个数定义为F_i，

G_n= F₁+ F₂+ F₃+ ... + F_n

根据搜索树性质，则当根节点的值为i时, 它的左子树为由 节点1 到节点i-1 组成的二叉搜索树，右子树为由 节点i + 1 到节点n 组成的二叉搜素树。

推到出： F_i= G_i-1* G_n-i

那么 G_n= G₀G_n-1+ G₁G_n-2+ G₂G_n-3+ ... + G_n-1G₀

原来G_n就是卡塔兰数！

实现：

这里用的是DP，先计算G₂，再计算G₃，一直到G_n。

 1 int CatalanNum(int n) {
 2     if(n <= 1){
 3         return 1;
 4     }
 5     int[] dp = new int[n + 1];
 6     dp[0] = 1;
 7     dp[1] = 1;
 8     for(int i = 2; i <= n; i++){
 9         for(int j = 1; j <= i; j++){
10             dp[i] += dp[j - 1] * dp[i - j];
11         }
12     }
13     return dp[n];
14 }

时间复杂度：（2 + n) * (n - 1) / 2, 也就是O(N²)。

空间复杂度：dp数组，O(N)。

通项公式：

果然，数学家又给出了通项公式：

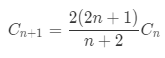
代码实现：

int CatalanNum (int n) {
    if(n == 0){
        return 1;
    }
    int[] dp = new int[n + 1];
    dp[0] = 1;
    for(int i = 0; i < n; i++){
        dp[i + 1] = dp[i] * 2*(2 * i + 1) / (i + 2);
    }
    return dp[n];
}

时间复杂度：（O(N)。

空间复杂度：dp数组，O(N)。（可以优化到O(1), 为什么我每次都不优化。。。）

最后提醒一下：卡特兰数增长非常快，建议使用大数类型。

PS:

最近看到很多简历都提到了Dijkstra，哇塞，真的很亮眼。下次写它。

End