P.S.:本文题目来自北京大学张浩威(张过亿)dalao的课件。
I.0/1背包
有n个物品,体积为m的背包,每个物品有一个价值vi,和体积ti,选
择若干物品,使得体积之和不超过m的情况下价值之和最大。
n<=1000,m<=10000。
普通0/1背包。
II.0/1背包+
n<=1000,vi<=10。
按照记忆化搜索的思路:
设x=当前物品编号,y=当前体积之和,z=当前价值之和
当x与z固定时,y越小越好。因此将x与z作为状态,将y作为dp的值。
O(nvi)
III.0/1背包++
n<=40
这道题和DP没什么关系。正解是折半搜索.
O(2^(n/2)*n) 折半搜索 所有物品分成两半,对两半分别进行搜索,一种方案 <==> 两边各取一个拼起来
IV.0/1背包+++
价值之和模p最大
n<=40 p<=10000
因为 (a+b+c)%p <==> ((a+b)%p+c)%p
因此价值vi<=10000 同时
O(np)
V.0/1背包++++
对于任意第i个物品,求第i个物品一定不在背包时的最大价值。
n<=1000,m<=10000。
一个物品k不在背包时的最大价值,相当于将最大价值分为1~k-1的最大价值与k+1~n的最大价值。
我们可以O(nm)的算出一个前缀的最大价值和一个后缀的最大价值。
然后枚举以下分割的体积,算出ans。
前i个物品,体积之和是j,价值之和最大是多少 一个前缀的物品集合 后缀的物品集合 假如第x个物品不在了,1~x-1 + x+1~n 一段和一段后缀。 它们分别被分配了多少体积。 枚举一下 枚举x,再枚举分配给了前缀多少体积,求max f[i][j] 1~i 体积为j最大价值 g[i][j] i~n 体积为j最大价值 for (x=1; x<=n; x++) { ans=0; for (j=0; j<=m; j++) ans=max(ans,f[x-1][j]+g[x+1][m-j]); cout<<ans<<endl; }
VI.0/1背包+++++
输出方案
• n<=10000,m<=10000。
• TL=2s
• ML=1M
一般0/1背包的输出方案
for (i=1; i<=n; i++) { for (j=0; j<=m; j++) { dp[i][j]=dp[i-1][j]; g[i][j]=j; if (j>=w[i]) if (dp[i-1][j-w[i]]+v[i]>dp[i][j]) { dp[i][j]=dp[i-1][j-w[i]]+v[i]; g[i][j]=j-w[i]; } } } // g[i][j] : dp[i][j] 由 dp[i-1][g[i][j]]转移得到 j=m; for (i=n; i>=1; i--) { if (j!=g[i][j]) 第i个物品被选择了 j=g[i][j]; }
然而本题非常良心的把内存设为1M,也就是说我们不能开二维数组,即只能用一维数组来存方案。
此处zhw介绍了一种精妙的做法:
g[i]表示dp[i][当前体积v]由dp[i/2][g[i]]转移得到,然后不断分治。
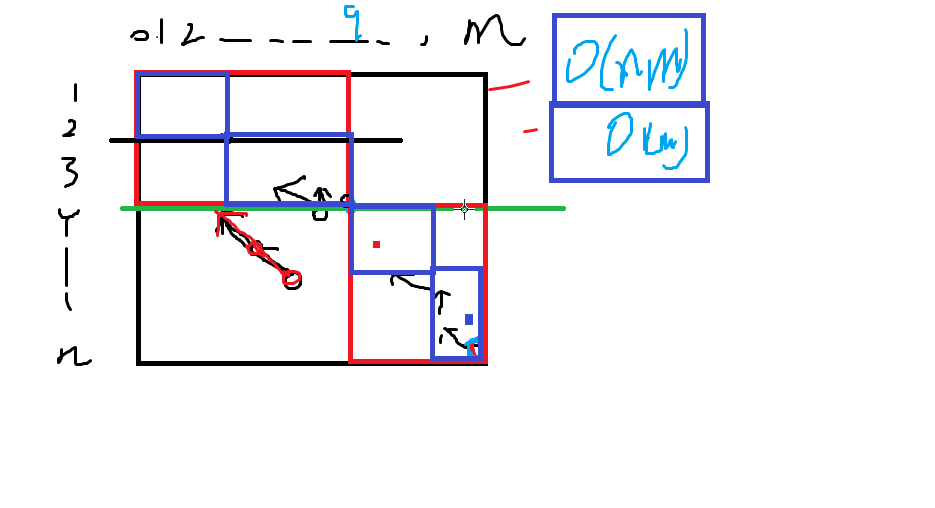
最终分割的矩形越来越小,最终形成一条从1到n的路径。
这样就在O(M)的空间复杂度内求出了最优方案。