减治法(reduceandconquermethod)在将原问题分解为若干个子问题后,利用了原问题的解与子问题的解之间的关系,
这种关系通常表现为:
(1)原问题的解只存在于其中一个较小规模的子问题中;
(2)原问题的解与其中一个较小规模的解之间存在某种对应关系。
由于原问题的解与较小规模的子问题的解之间存在这种关系,
所以,只需求解其中一个较小规模的子问题就可以得到原问题的解,无须对子问题的解进行合并。
因此,严格地说,减治法应该是一种退化了的分治法。
减治法主要有以下三种类型:
(1)减常量
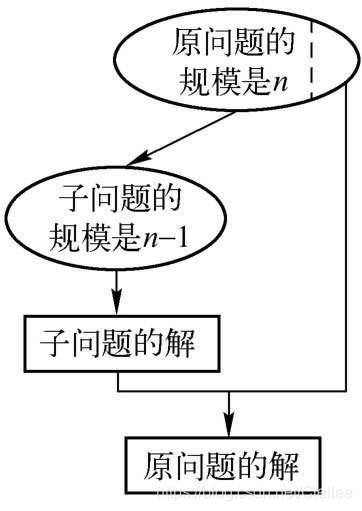
算法每次迭代总是从实例规模中减去一个相同的常量,一般来说,这个常量等于1。
直接插入排序、拓扑排序等都是减1技术的应用实例。
(2)减常数因子
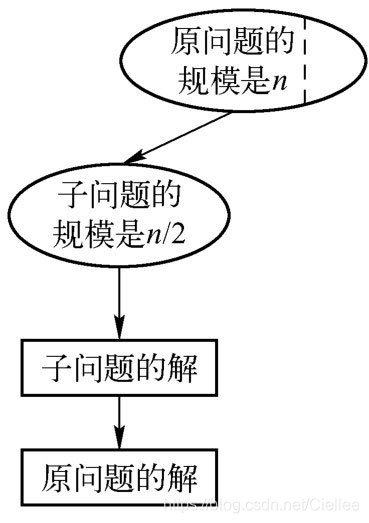
算法每次迭代总是从实例规模中减去一个相同的常数因子,一般来说,这个常数因子等于2(即减半)。
折半查找、平衡二叉树的查找、B树的查找、堆调整等都是减半技术的应用实例。
(3)减可变规模
算法每次迭代时减去的规模都是不同的。
欧几里得算法、二叉排序树的查找等都是减可变规模的应用实例。
算法设计实例——假币问题
【问题】 在n枚外观相同的硬币中有一枚是假币,并且已知假币较轻。
可以通过一架天平来任意比较两组硬币,从而得知两组硬币的重量是否相同,或者哪一组更轻一些。
假币问题是要求设计一个高效的算法来找出这枚假币。
【想法】 问题的解决是经过一系列比较和判断,最自然的想法就是一分为二,也就是把n枚硬币分成两组,每组有└n/2」枚硬币,如果n为奇数,就留下一枚硬币,然后把两组硬币分别放到天平的两端。如果两组硬币的重量相同,那么留下的硬币就是假币;否则,用同样的方法对较轻的那组硬币进行同样的处理,因为假币一定在较轻的那组里。由于每次用天平比较后,只需解决一个规模减半的问题,所以,它属于减治算法。该算法在最坏情况下的时间性能满足如下递推式:

通用分治递推式的定理,得到T(n)=O(log2^n)。
实际上,减半不是一个最好的选择。考虑不是把硬币分成两组,而是分成三组,前两组有「n/3┐个硬币,其余的硬币作为第三组;将前两组硬币放到天平上,如果它们的重量相同,则假币一定在第三组中,用同样的方法对第三组进行处理;如果前两组的重量不同,则假币一定在较轻的那一组中,用同样的方法对较轻的那组硬币进行处理。
显然这个算法存在递推式:
这个递推式的解是T(n)=O(log3n)。这个减治法是将原问题一分为三,从而获得了更少的比较次数。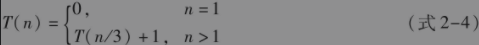

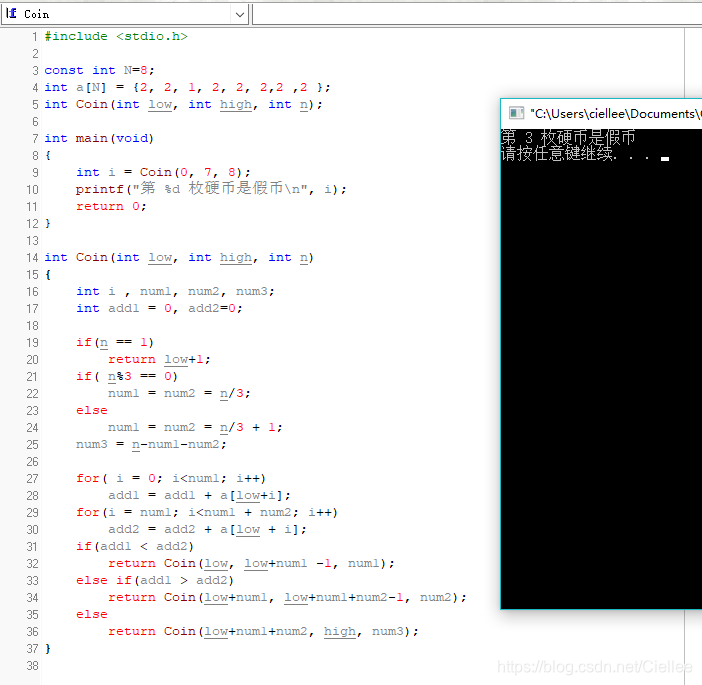
设N枚硬币的重量存储在数组a[N]中,函数Coin实现假币问题的求解,参数low和high分别表示假币所在的数组下标范围,为避免传递数组参数,将a[N]设为全局变量。
程序如下:
#include <stdio.h>
constintN = 8;
int a[N] = {2, 2, 1, 2, 2, 2,2 ,2 };
int Coin(int low, int high, int n);
int main(void)
{
int i = Coin(0, 7, 8);
printf("第 %d 枚硬币是假币\n", i);
return 0;
}
int Coin(int low, int high, int n)
{
int i , num1, num2, num3;
int add1 = 0, add2=0;
if(n == 1)
return low+1;
if( n%3 == 0)
num1 = num2 -n/3;
num3 = n-num1-num2;
for( i = 0; i<num1; i++)
add1 = add1 + a[low+i];
for(i = num1; i<num1 + num2; i++)
add2 = add2 + a[low + i];
if(add1 < add2)
return Coin(low, low+num1 -1, num1);
elseif(add1 > add2)
return Coin(low+num1, low+num1+num2-1, num2);
else
Coin(low+num1+num2, high, num3);
}