【LeetCode每日一练】78. 子集（中等|JS|回溯算法）

一、题目描述

二、解题思路

经典的递归回溯思想的题目，先贴两张图，第一张，我们只看每个元素，都有两种选择，选入子集和不选入子集，那么我们就可以考察当前的数，在选择它的基础上继续选下去，或者在不选择它的基础上（开辟另一个分支），继续选下去。那么就用指针index代表当前递归考察的数字，当index超出数组长度（越界了），那么表示所有数字都考察完毕，把当前子集加入解集res，结束当前递归的分支。

当然这里还需要回溯，在结束当前递归后，撤销当前选择的数字，回到选择前的状态，继续做另一个选择（即不选当前的数，基于不选，往下递归，继续生成子集），在不断回溯下得出所有的解。

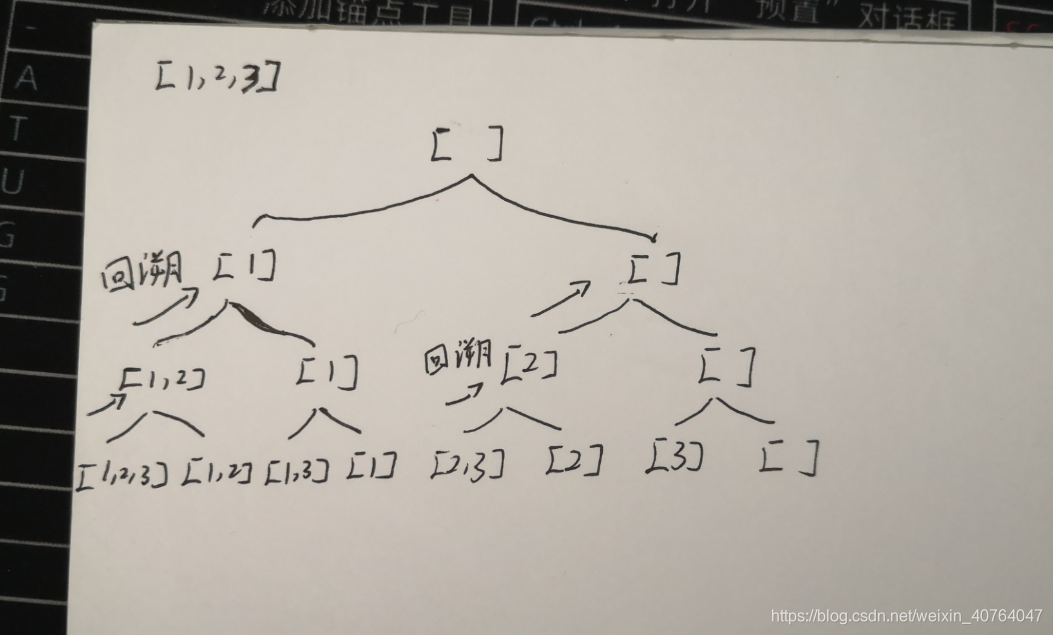
第二张图是为了理解回溯而跟着代码一步一步走的笔记，除了我自己别人应该都看不懂~搞了好久才明白怎么实现的。

三、代码实现

var subsets = function(nums) {
    
    
  const res = []
  const dfs = (index,list)=>{
    
    
    if(index == nums.length){
    
    
      res.push(list.slice())
      return
    }
    list.push(nums[index])
    dfs(index+1,list)
    list.pop()
    dfs(index+1,list)
  }
  dfs(0,[])
  return res
};

代码虽然比较简单，但还是花了不少时间去理解（太菜了。。。）

官方题解还有一种位运算的方法，这里就先不写了，改天有时间再补充。