A. Bovine Dilemma
题意:任意2点距离的种数
思路:暴力枚举即可
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=1e5+10;
int a[N];
bool vis[N];
int main(){
int T;
scanf("%d",&T);
while(T--){
memset(vis,0,sizeof vis);
int n;
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
}
int cnt=0;
for(int i=1;i<=n;i++)
for(int j=i+1;j<=n;j++){
int d=a[j]-a[i];
if(!vis[d])cnt++;
vis[d]=1;
}
cout<<cnt<<endl;
}
return 0;
}
B. Last minute enhancements
题意:一段音符 你可以对一个音符进行+1或者不进行操作 问你种类最多是多少
思路:贪心 先排序再进行处理 优先把大的+1 如果增大不会减少次数 那么就将他+1
wa了2发数组开小了 差点这场又没了 还没找到啥错误 幸好及时发现
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=2e5+10;
int a[N];
int vis[N];
bool cmp(int x,int y){
return x>y;
}
int main(){
int T;
scanf("%d",&T);
while(T--){
memset(vis,0,sizeof vis);
int n;
scanf("%d",&n);
int cnt=0;
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
if(!vis[a[i]])cnt++;
vis[a[i]]++;
}
sort(a+1,a+1+n,cmp);
for(int i=1;i<=n;i++){
int pre=cnt;
vis[a[i]+1]++;
vis[a[i]]--;
if(vis[a[i]+1]==1)cnt++;
if(vis[a[i]]==0)cnt--;
a[i]++;
if(pre<=cnt)continue;
else{
a[i]--;
vis[a[i]+1]--;
vis[a[i]]++;
cnt++;
}
}
cout<<cnt<<endl;
}
return 0;
}
C. Canine poetry
题意:给出一段字符串 能对字母进行修改 问最少多少次能将整个字符串变为 不含任何回文串
思路:从前往后只要比较这个字符前面存在的位置 如果<=2那么将修改次数+1
否则将存在位置改为当前
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=2e5+10;
int pre[50];
char a[N];
int main(){
int T;
cin>>T;
while(T--){
cin>>a+1;
memset(pre,0,sizeof pre);
int ans=0;
int len=strlen(a+1);
for(int i=1;i<=len;i++){
int u=a[i]-'a';
if(pre[u]&&i-pre[u]<=2)ans++;
else pre[u]=i;
}
cout<<ans<<endl;
}
}
D. 13th Labour of Heracles
题意:分别组成1、2、3…n-1个联通块 分别组成联通块时的权值和最大值是多少 权值的计算方法为 这个联通块所有点的权值和
思路:只有度数大于1的节点可以和别的点组成多次联通块 说起来其实是个贪心
将权值排序 然后优先选择权值大的
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=2e5+10;
typedef long long LL;
pair<int,int> a[N];
int d[N];
bool cmp(pair<int,int> x,pair<int,int> y){
return x>y;
}
int main(){
int T;
cin>>T;
while(T--){
int n;
scanf("%d",&n);
LL ans=0,sum=0;
memset(d,0,sizeof d);
for(int i=1;i<=n;i++){
scanf("%d",&a[i].first);
a[i].second=i;
sum+=a[i].first;
}
for(int i=1;i<n;i++){
int u,v;
scanf("%d%d",&u,&v);
d[u]++;
d[v]++;
}
sort(a+1,a+1+n,cmp);
int cnt=0;
cout<<sum<<" ";
for(int i=0;i<=n;i++){
int u=a[i].second;
if(d[u]==1)continue;
while(d[u]>1){
sum+=a[i].first;
cout<<sum<<" ";
d[u]--;
}
}
puts("");
}
}
E. Apollo versus Pan
题意:给出一段数列 x
求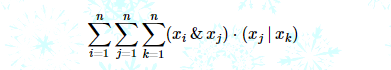
思路 首先预处理60位 中每一位 1的个数
然后我们可以从前往后枚举即 i从1 - n枚举中间的xj数
j从0到60对他每一位进行枚举
从左边看
如果这一位为1
那么 res1+=(1<<j)*v[j];
如果为0
那么res1+=0;
从右边看
如果为1
那么 res2+=(1<<j)*n;
如果为0
那么 res2+=(1<<j)v[j];
然后ans+=(res1res2);就为结果
(取膜略)
这种题就是一种套路 求每一个数的贡献
#include<iostream>
#include<cstring>
#include<algorithm>
#include<vector>
using namespace std;
const int N=5e5+10,mod=1e9+7;
typedef long long LL;
LL a[N];
int v[70];
int main(){
int T;
scanf("%d",&T);
while(T--){
int n;
scanf("%d",&n);
LL ans=0;
memset(v,0,sizeof v);
for(int i=1;i<=n;i++){
scanf("%lld",&a[i]);
for(int j=0;j<60;j++)//第j位为1的个数
v[j]+=a[i]>>j&1;
}
for(int i=1;i<=n;i++){
LL res1=0,res2=0;
for(int j=0;j<60;j++){
if(a[i]>>j&1)
res1=(res1+1ll*(1ll<<j)%mod*v[j]%mod)%mod;
}
for(int k=0;k<60;k++){
if(a[i]>>k&1)res2=(res2+(1ll<<k)%mod*n%mod)%mod;
else res2=(res2+(1ll<<k)%mod*v[k]%mod)%mod;
}
ans=(ans+res1*res2%mod)%mod;
}
cout<<ans<<endl;
}
}
B题耽误了我30多分钟 以后注意数组范围 优先开1e6
比起上次爆0 这次还是好多了 但是F题看都没看
多打比赛才能提升水平
留下ID我们一起打cf 我的qq 5349428