文章目录
1.符号对象
- 符号对象的建立
- 符号对象的运算
- 符号矩阵
1.符号对象的确立
(1)sym函数
sym函数用于建立单个符号对象,其常用调用格式为:
符号对象名=sym(A)
符号计算的结果是一个精确的数学表达式。 数值计算的结果是一个数值。
(2)syms命令
syms命令可以一次定义多个符号变量,其一般调用格式如下:
syms 符号变量名1 符号变量名2 … 符号变量名n
2. 符号对象的运算
(1)四则运算
运算结果依然是一个符号表达式
(2)关系运算
6种关系运算符:<、<=、>、>=、==、~=。
对应的6个函数:lt()、le()、gt()、ge()、eq()、ne()。
在进行符号对象的运算前,可用assume函数对符号对象设置值域,
函数调用格式为:
assume(condition) assume(expr,set)
第一种格式指定变量满足条件condition,第二种格式指定表达式
expr属于集合set。
(3)逻辑运算
3种逻辑运算符:&(与)、|(或)和~(非)。
4个逻辑运算函数:and(a,b)、or(a,b)、not(a)和xor(a,b)。
>> syms x;
>> y=x>0 & x<10
y=
0<x & x<10
(4)因式分解和展开计算
MATLAB提供了符号表达式的因式分解与展开的函数,函数的调用格式为:
① factor(s):对符号表达式s分解因式。
② expand(s):对符号表达式s进行展开。
③ collect(s):对符号表达式s合并同类项。
④ collect(s,v):对符号表达式s按变量v合并同类项
(5)其他运算
① 提取有理分式的分子分母:[n,d]=numden(s)。
② 提取符号表达式的系数:c=coeffs(s,x)。
③符号表达式化简:simplify(s)。
④ 符号多项式与多项式系数向量之间的转换:
- 符号多项式转换为多项式系数向量p=sym2poly(s)。
- 多项式系数向量转换为符号多项式:s=poly2sym( p )。
3. 符号矩阵
符号矩阵也是一种符号表达式,所以符号表达式运算都可以在矩阵意
义下进行。
- 注意:这些函数作用于符号矩阵时,是分别作用于矩阵的每一个元素。
- 例如:建立符号矩阵并化简
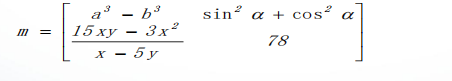
>> syms a b x y alp;
>> m=[a^3-b^3,sin(alp)^2+cos(alp)^2;(15*x*y-3*x^2)/(x-5*y),78]
m =
[ a^3 - b^3,cos(alp)^2 + sin(alp)^2]
[(- 3*x^2 + 15*y*x)/(x - 5*y), 78]
>> simplify(m)
ans =
[ a^3 - b^3, 1]
[ -3*x, 78]
- 例2 当λ取何值时,以下齐次线性方程组有非零解。
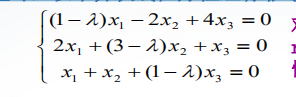
syms lamda;
A=[1-lamda,-2,4;2,3-lamda,1;1,1,1-lamda];
D=det(A);
factor(D)
程序运行结果为:
ans =
[-1, lamda, lamda - 2, lamda - 3]
从而得知,当λ=0、λ=2或λ=3时,原方程组有非零解。