LearnOpenGL学习笔记—高级光照 01~02：高级光照/Gamma校正

【项目地址：点击这里这里这里】

1 高级光照

本节对应官网学习内容：高级光照
官网基本就是讲Blinn-Phong，在入门的时候自己就额外做过了
所以附上当时的笔记：LearnOpenGL学习笔记—光照02：Lighting Basis/Advanced Lighting

2 Gamma校正

本节对应官网学习内容：Gamma校正
中文版说是未进行完全的重写，错误可能会很多，推荐对照原文。

所以以下内容相当于自己对照着中文和英文翻译着理解的产物

当我们最后计算完场景内像素的颜色后，我们就要把它们显示在监视器上了。在数字图像的往昔时代，大部分显示器都是阴极射线管显示器（CRT）。

这些显示器有一些物理特性，输入两倍高的电压后不会产生亮度的两倍变化。

输入电压加倍后，对应到亮度上，亮度变化大概是会呈现原先的2.2倍的指数变化，这也叫做显示器的Gamma值。

• 官网译注：
  Gamma也叫灰度系数，每种显示设备都有自己的Gamma值，都不相同，有一个公式：设备输出亮度 = 电压的Gamma次幂。
  任何设备Gamma基本上都不会等于1，等于1是一种理想的线性状态，这种理想状态是：如果电压和亮度都是在0到1的区间，那么多少电压就等于多少亮度。
  对于CRT，Gamma通常为2.2，因而，输出亮度 = 输入电压的2.2次幂。
  在接下来第二张的曲线图中看到Gamma2.2的效果在实际显示出来后，总会比预期暗，相反Gamma0.45就会比理想预期亮。
  如果将Gamma0.45叠加到Gamma2.2的显示设备上，便会对偏暗的显示效果做到校正，这个简单的思路就是本节的核心。

显示器的Gamma与人眼对亮度的感知关系很巧妙的形成了一种类似的（逆）幂关系。
如下面这张图所示

第一行是人眼感知的正常灰阶，两倍的亮度变化才会事实上有两倍的差异。

• 我们在看第一行颜色值从0到1（从黑到白）的过程中，亮度要增加一倍，我们才会感受到明显的颜色变化（变亮一倍）。
• 打个比方：颜色值从0.1到0.2，我们会感受到一倍的颜色变化，而从0.4到0.8我们才能感受到相同程度（变亮一倍）的颜色变化。

然而，当我们谈论光的物理亮度，比如光源发射光子的数量的时候，底部第二行的灰阶显示，才是物理世界真实的亮度。

扫描二维码关注公众号，回复： 12723048 查看本文章

如底部的灰阶显示，亮度加倍时返回的也是真实的物理亮度。

• 官网译注：
  这里亮度是指光子数量和正相关的亮度，即物理亮度，前面讨论的是人的感知亮度。
  物理亮度和感知亮度的区别在于，物理亮度基于光子数量，感知亮度基于人的感觉，比如第二个灰阶里亮度0.1的光子数量是0.2的二分之一）。
  但是由于这与我们的眼睛感知亮度不完全一致（对比较暗的颜色变化更敏感），所以它看起来有差异。

因为人眼看到颜色的亮度更倾向于顶部的灰阶，显示器使用的也是同一种指数关系（电压的2.2次幂），所以物理亮度通过监视器能够被映射到顶部的非线性亮度；因此看起来效果不错

• 官网译注：
  CRT亮度是是电压的2.2次幂而人眼相当于2次幂，因此CRT这个缺陷正好能满足人的需要。

显示器的这个非线性映射，的确可以让亮度在我们眼中看起来更好。
但当渲染图像时，会产生一个问题：
我们在应用中配置的亮度和颜色是基于监视器所看到的，这样所有的配置实际上是非线性的亮度/颜色配置
如下图

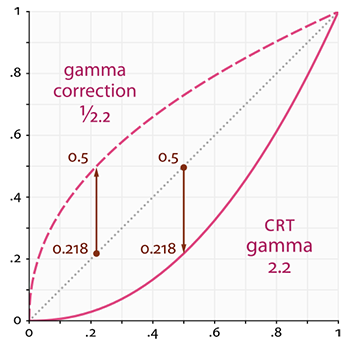
• 中间的点线代表线性颜色/亮度值=1，表示的是理想状态，Gamma为1，也就是在线性空间中
  实线表示的是显示器表示的颜色空间
• 我们在线性空间里加倍颜色，它确实会让值也加倍
  比如，颜色向量$\overline{L}=(0.5,0.0,0.0)$代表的是暗红色。
  如果我们在线性空间中把它翻倍，就会变成$(1.0,0.0,0.0)$，就像你图中看到的那样的线性关系
• 然而，当我们把$\overline{L}=(0.5,0.0,0.0)$显示在显示器上时，我们从图里看，会觉得它显示出了$(0.218,0.0,0.0)$，然而我们需要的是$(1.0,0.0,0.0)$。
• 在这儿问题就出现了：当我们将理想中直线上的那个暗红色翻一倍时，在监视器上实际上需要翻了4.5倍以上才有一样的效果

直到现在，我们还一直假设我们所有的工作都是在线性空间中进行的（Gamma为1）。

但是我们实际上是工作在显示器的输出空间上的，所以我们配置的所有颜色和光照变量从物理角度来看都是不正确的，显示器很少显示正确。

出于这个原因，我们（以及艺术家）通常会将光照值设置得比本来更亮一些（因为监视器会将其亮度显示的更暗一些），如果不是这样，在线性空间里计算出来的光照就会不正确。

同时，还要记住，监视器所显示出来的图像和线性图像的最小亮度是相同的，它们最大的亮度也是相同的；只是中间亮度部分会被压暗。

因为所有中间亮度都是线性空间的关系计算出来的（计算的时候假设Gamma为1），显示器显示以后，实际上都会不正确。
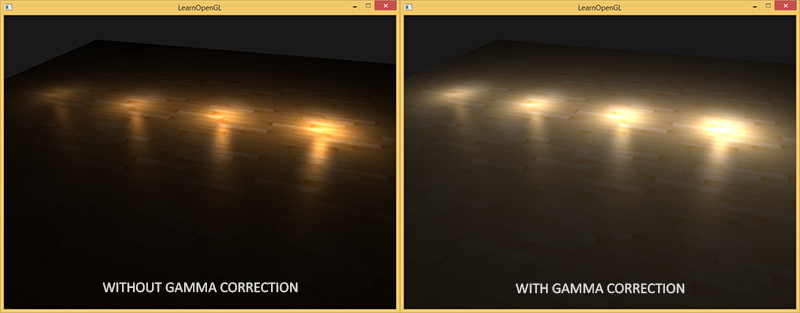
当使用更高级的光照算法时，这个问题会变得越来越明显，可以看看下图：

可以看到，使用gamma校正更新的颜色值可以更好显示，较暗的区域有显示更多细节。
总的来说，通过一个小修改得到了一个更好的图像质量。

如果不校正这个监视器gamma，灯光看起来是错误的，艺术家将很难获得逼真和好看的效果。

2.1 应用gamma矫正

Gamma校正(Gamma Correction)的思路是在最终的颜色输出上应用监视器Gamma的倒数。

回头看前面的Gamma曲线图，会有一个短划线，它是监视器Gamma曲线的翻转曲线。

我们在颜色显示到监视器的时候把每个颜色输出都加上这个翻转的Gamma曲线，这样应用了监视器Gamma以后最终的颜色将会变为线性的。

虽然在短划线里，我们所得到的中间色调就会更亮，但是监视器使它们变暗，最后就是平衡回来了。

我们来看另一个例子。还是那个暗红色$(0.5,0.0,0.0)$。
在将颜色显示到监视器之前，我们先对颜色应用Gamma校正曲线。
线性的颜色显示在监视器上相当于降低了2.2次幂的亮度，所以倒数就是1/2.2次幂。
Gamma校正后的暗红色就会成为
$(0.5,0.0,0.0{)}^{1/2.2}=(0.5,0.0,0.0{)}^0.45=(0.73,0.0,0.0)$
校正后的颜色接着被发送给监视器，最终显示出来的颜色是$(0.73,0.0,0.0{)}^2.2=(0.5,0.0,0.0)$
使用了Gamma校正，监视器最终会显示出我们在应用中设置的那种线性的颜色。

• 2.2通常是是大多数显示设备的大概平均gamma值。
• 基于gamma2.2的颜色空间叫做sRGB颜色空间。
• 每个监视器的gamma曲线都有所不同，但是gamma2.2在大多数监视器上表现都不错。出于这个原因，游戏经常都会为玩家提供改变游戏gamma设置的选项，以适应每个监视器
• 注：现在Gamma2.2相当于一个标准，后文中会看到。
• 但现在可能会问，前面不是说Gamma2.2看起来不是正好适合人眼么，为何还需要校正。这是因为在程序中设置的颜色，比如光照都是基于线性Gamma，即Gamma1，所以理想中的亮度和实际表达出的不一样，如果要表达出理想中的亮度就要对这个光照进行校正。

有两种在场景中应用gamma校正的方式：

2.1.1 应用1：使用OpenGL内建的sRGB帧缓冲

首先是使用OpenGL内建的sRGB帧缓冲。 自己在像素着色器中进行gamma校正。

第一个选项也许是最简单的方式，但是我们也会丧失一些控制权。
开启GL_FRAMEBUFFER_SRGB，可以告诉OpenGL每个后续的绘制命令里，在颜色储存到颜色缓冲之前先校正sRGB颜色。
sRGB这个颜色空间大致对应于gamma2.2，它也是家用设备的一个标准。
开启GL_FRAMEBUFFER_SRGB以后，每次像素着色器运行后续帧缓冲，OpenGL将自动执行gamma校正，包括默认帧缓冲。

开启GL_FRAMEBUFFER_SRGB简单的调用glEnable就行：

glEnable(GL_FRAMEBUFFER_SRGB);

自此，渲染的图像就被进行gamma校正处理，不需要做任何事情硬件就帮我们处理了。

但是要记住：gamma校正将把线性颜色空间转变为非线性空间，所以在最后一步进行gamma校正是极其重要的。

如果我们在最后输出之前就进行gamma校正，所有的后续操作都是在操作不正确的颜色值。

例如，如果我们使用多个帧缓冲，我们会希望这样：
让两个帧缓冲之间传递的中间结果仍然保持线性空间颜色，只是给发送给监视器的最后的那个帧缓冲应用gamma校正。

2.1.2 应用2：手动操作

第二个方法稍微复杂点，但同时也是我们对gamma操作有完全的控制权。

我们在每个相关像素着色器运行的最后应用gamma校正，所以在发送到帧缓冲前，颜色就被校正了。

void main()
{
    
    
    // do super fancy lighting 
    [...]
    // apply gamma correction
    float gamma = 2.2;
    fragColor.rgb = pow(fragColor.rgb, vec3(1.0/gamma));
}

最后一行代码，将fragColor的每个颜色元素应用有一个1.0/gamma的幂运算，校正像素着色器的颜色输出。

这个方法有个问题就是为了保持一致，我们必须在像素着色器里加上这个gamma校正。

所以如果我们有很多像素着色器，它们可能分别用于不同物体，那么我们就必须在每个着色器里都加上gamma校正了。

一个更简单的方案是在渲染循环中引入后处理阶段，在后处理四边形上应用gamma校正，这样我们只要做一次就好了（fbo的shader）。

这些单行代码代表了gamma校正的实现。
不太令人印象深刻，但当我们进行gamma校正的时候有一些额外的事情别忘了考虑。

2.2.1 注意点1：sRGB纹理

因为监视器总是在sRGB空间中显示应用了gamma的颜色，无论什么时候，当我们在计算机上绘制、编辑或者画出一个图片的时候，我们所选的颜色都是根据我们在监视器上看到的那种。

这实际意味着所有我们创建或编辑的图片并不是在线性空间，而是在sRGB空间中（注：sRGB空间定义的gamma接近于2.2），假如在我们的屏幕上对暗红色翻一倍，便是根据我们所感知到的亮度进行的，并不等于将红色元素加倍。

结果就是纹理编辑者，所创建的所有纹理都是在sRGB空间中的纹理，所以如果我们在渲染应用中使用这些纹理，我们必须考虑到这点。

在我们应用gamma校正之前，这不是个问题，因为纹理在sRGB空间创建和展示，同样我们还是在sRGB空间中使用，从而不必gamma校正纹理显示也没问题。

然而，现在我们是把所有东西都放在线性空间中展示的，纹理颜色就会变坏，如下图展示的那样：

纹理图像实在太亮了，发生这种情况是因为，它们实际上进行了两次gamma校正！

想一想，当我们基于监视器上看到的情况创建一个图像，我们就已经对颜色值进行了gamma校正，所以再次显示在监视器上就没错。

由于我们在渲染中又进行了一次gamma校正，图片就实在太亮了。

为了修复这个问题，我们得确保纹理制作者是在线性空间中进行创作的。

但是，由于大多数纹理制作者并不知道什么是gamma校正，并且在sRGB空间中进行创作更简单，这也许不是一个好办法。

另一个解决方案是重校，或把这些sRGB纹理在进行任何颜色值的计算前变回线性空间。我们可以这样做：

float gamma = 2.2;
vec3 diffuseColor = pow(texture(diffuse, texCoords).rgb, vec3(gamma));

为每个sRGB空间的纹理做这件事非常烦人。
幸好，OpenGL给我们提供了另一个方案来解决我们的麻烦，这就是GL_SRGB和GL_SRGB_ALPHA内部纹理格式。

如果我们在OpenGL中创建了一个纹理，把它指定为以上两种sRGB纹理格式其中之一，OpenGL将自动把颜色校正到线性空间中，这样我们所使用的所有颜色值都是在线性空间中的了。我们可以这样把一个纹理指定为一个sRGB纹理：

glTexImage2D(GL_TEXTURE_2D, 0, GL_SRGB, width, height, 0, GL_RGB, GL_UNSIGNED_BYTE, image);

如果还打算在纹理中引入alpha元素，必须将纹理的内部格式指定为GL_SRGB_ALPHA。

因为不是所有纹理都是在sRGB空间中的，所以当我们把纹理指定为sRGB纹理时要格外小心。

比如diffuse纹理，这种为物体上色的纹理几乎都是在sRGB空间中的。

而为了获取光照参数的纹理，像specular贴图和法线贴图几乎都在线性空间中，所以如果把它们也配置为sRGB纹理的话，光照就坏掉了。

指定sRGB纹理时要当心。

将diffuse纹理定义为sRGB纹理之后，我们将获得我们所期望的视觉输出，这次每个物体都会只进行一次gamma校正。

2.2.2 注意点2：衰减

在使用了gamma校正之后，另一个不同之处是光照衰减(Attenuation)。真实的物理世界中，光照的衰减和光源的距离的平方成反比。

float attenuation = 1.0 / (distance * distance);

然而，当我们使用这个衰减公式的时候，衰减效果总是过于强烈，光只能照亮一小圈，看起来并不真实。
出于这个原因，我们使用在基本光照教程中所讨论的那种衰减方程，它给了我们更大的控制权，此外我们还可以使用双曲线函数：

float attenuation = 1.0 / distance;

双曲线比使用二次函数变体在不用gamma校正的时候看起来更真实，不过但我们开启gamma校正以后线性衰减看起来太弱了，符合物理的二次函数突然出现了更好的效果。下图显示了其中的不同：

这种差异产生的原因是，光的衰减方程改变了亮度值，而且屏幕上显示出来的不是线性空间，所以在监视器上效果最好的衰减方程，并不是符合物理的。

想想平方衰减方程，如果我们使用这个方程，而且不进行gamma校正，显示在监视器上的衰减方程实际上将变成$(1.0/distanc{e}^2{)}^{2.2}$。

若不进行gamma校正，将产生更强烈的衰减。这也解释了为什么双曲线不用gamma校正时看起来更真实，因为它实际变成了$(1.0/distance{)}^{2.2}=1.0/distanc{e}^{2.2}$。这和物理公式是很相似的。

我们在基础光照教程中讨论的更高级的那个衰减方程在有gamma校正的场景中也仍然有用，因为它可以让我们对衰减拥有更多准确的控制权（不过，在进行gamma校正的场景中当然需要不同的参数）。

总而言之，gamma校正使我们可以在线性空间中进行操作。

因为线性空间更符合物理世界，大多数物理公式现在都可以获得较好效果，比如真实的光的衰减。

我们的光照越真实，使用gamma校正获得漂亮的效果就越容易。

这也正是为什么当引进gamma校正时，建议只去调整光照参数的原因。

3 实践

我们在学了帧缓冲之后做的场景都加入了后处理，所以我们在后处理阶段使用gamma校正
也就是在screenShader的片段着色器最后加上

  float gamma = 2.2;
  FragColor.rgb = pow(FragColor.rgb, vec3(1.0/gamma));

调整需要的diffuse材质变成GL_SRGB_ALPHA
也就是glTexImage2D的第三个参数变为GL_SRGB_ALPHA
比如这样

LoadImageToGPU("container2.png", GL_SRGB_ALPHA, GL_RGBA),

然后我们也修改Model.cpp的函数（可以从以前的复习总结中获取这个文件），在其中加入对于diffuse材质的判断

unsigned int Model::TextureFromFile(const char *path, const std::string &directory, std::string typeName)
{
    
    
	std::string filename = std::string(path);
	filename = directory + '\\' + filename;

	unsigned int textureID;
	glGenTextures(1, &textureID);

	int width, height, nrComponents;
	unsigned char *data = stbi_load(filename.c_str(), &width, &height, &nrComponents, 0);
	if (data)
	{
    
    
		GLenum format;
		GLenum iformat;
		if (nrComponents == 1) {
    
    
			format = GL_RED;
			iformat = GL_RED;
		}
		else if (nrComponents == 3) {
    
    
			format = GL_RGB;
			iformat = GL_RGB;
		}
		else if (nrComponents == 4 && typeName == "texture_diffuse"){
    
    
			format = GL_RGBA;
			iformat = GL_SRGB_ALPHA;
		}
		else {
    
    
			format = GL_RGBA;
			iformat = GL_RGBA;
		}
		glBindTexture(GL_TEXTURE_2D, textureID);
		glTexImage2D(GL_TEXTURE_2D, 0, iformat, width, height, 0, format, GL_UNSIGNED_BYTE, data);
		glGenerateMipmap(GL_TEXTURE_2D);

		glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_S, GL_REPEAT);
		glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_T, GL_REPEAT);
		glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_LINEAR_MIPMAP_LINEAR);
		glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_LINEAR);

		stbi_image_free(data);
	}
	else
	{
    
    
		std::cout << "Texture failed to load at path: " << path << std::endl;
		stbi_image_free(data);
	}

	return textureID;
}

以及天空盒也要调整，防止二次校正

glTexImage2D(GL_TEXTURE_CUBE_MAP_POSITIVE_X + i,
				0, GL_SRGB_ALPHA, width, height, 0, GL_RGB, GL_UNSIGNED_BYTE, data
			);

以下是对比，这个是没有开启gamma校正的图

在同一环境下，做了如上开启gamma校正的操作后，我们对diffuse操作的颜色值都是在线性空间中的了，得到的结果可以说是正确了