【LR与SVM -2】SVM

1、SVM主要解决什么问题

SVM的全称是Support Vector Machine，即支持向量机，

主要用于解决模式识别领域中的数据分类问题，属于有监督学习算法的一种。

SVM要解决的问题可以用一个经典的二分类问题加以描述。

如上图所示，红色和蓝色的二维数据点显然是可以被一条直线分开的，在模式识别领域称为线性可分问题。

然而将两类数据点分开的直线显然不止一条。图1(b)和©分别给出了A、B两种不同的分类方案，其中黑色实线为分界线，术语称为“决策面”。

每个决策面对应了一个线性分类器。虽然在目前的数据上看，这两个分类器的分类结果是一样的，但如果考虑潜在的其他数据，则两者的分类性能是有差别的。

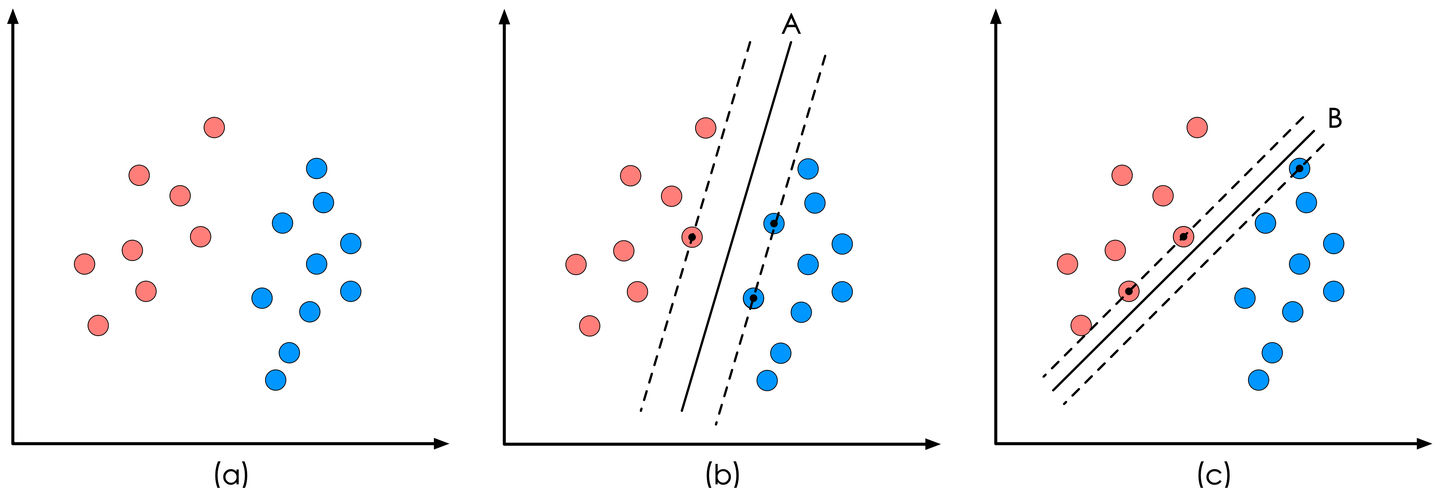
SVM算法认为图1中的分类器A在性能上优于分类器B，其依据是A的分类间隔比B要大。

这里补充下——什么是分类间隔：

扫描二维码关注公众号，回复： 13124869 查看本文章

保证决策面方向不变且不会出现错分样本的情况下移动决策面，会在原来的决策面两侧找到两个极限位置（越过该位置就会产生错分现象），如虚线所示。

虚线的位置由决策面的方向和距离原决策面最近的几个样本的位置决定。

而这两条平行虚线正中间的分界线就是在保持当前决策面方向不变的前提下的最优决策面。

两条虚线之间的垂直距离就是这个最优决策面对应的分类间隔。

对于这个真正的最优解对应的两侧虚线所穿过的样本点，就是SVM中的支持样本点，称为“支持向量”。

例如：上图中，A决策面就是SVM寻找的最优解，而相应的三个位于虚线上的样本点在坐标系中对应的向量就叫做支持向量。

在这里总结一下：

从表面上看，我们优化的对象似乎是这个决策面的方向和位置。

但实际上最优决策面的方向和位置完全取决于选择哪些样本作为支持向量。

而在经过漫长的公式推导后，你最终会发现，其实与线性决策面的方向和位置直接相关的参数都会被约减掉，最终结果只取决于样本点的选择结果。

2、线性SVM算法的数学建模

一个最优化问题通常有两个最基本的因素：

1）目标函数，也就是你希望什么东西的什么指标达到最好；

2）优化对象，你期望通过改变哪些因素来使你的目标函数达到最优。

在线性SVM算法中，目标函数显然就是那个**“分类间隔”，而优化对象则是决策面**。所以要对SVM问题进行数学建模，首先要对上述两个对象（“分类间隔”和“决策面”）进行数学描述。按照一般的思维习惯，我们先描述决策面。

2.1 决策面方程

先不要纠结于n维空间中的n-1维超平面这种超出正常人想象力的情景。

我们就老老实实地看看二维空间中的一根直线，我们从初中就开始学习的直线方程形式很简单。
$y=ax+b$ (2.1)

现在我们做个小小的改变，让原来的$x$轴变成$x_1$轴，$y$变成$x_2$轴，于是公式(2.1)中的直线方程会变成下面的样子

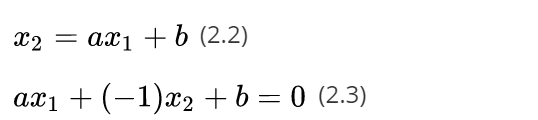
公式（2.3）的向量形式可以写成

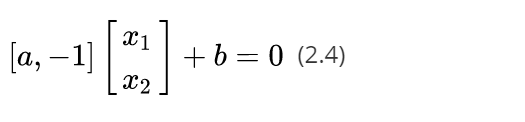
考虑到我们在等式两边乘上任何实数都不会改变等式的成立，所以我们可以写出一个更加一般的向量表达形式:

看到变量$w,x$略显粗壮的身体了吗？

他们是黑体，表示变量是个向量，表示变量是个向量，[一般我们提到向量的时候，都默认他们是个列向量。

就着公式(2.5)，我们再稍稍尝试深入一点。那就是探寻一下向量$w=[w_1,w_2{]}^T$和$r$的几何意义是什么？

因为我们是由一条直线推导出来的，由直线的基本性质，我们可以知道：

$w$就是斜率，它控制了直线的方向。

$r$就是截距，它控制了直线的位置。

2.2 分类“间隔”的计算模型

我们在2.1里介绍过分类间隔的定义及其直观的几何意义。

间隔的大小实际上就是支持向量对应的样本点到决策面的距离的二倍，下图所示。

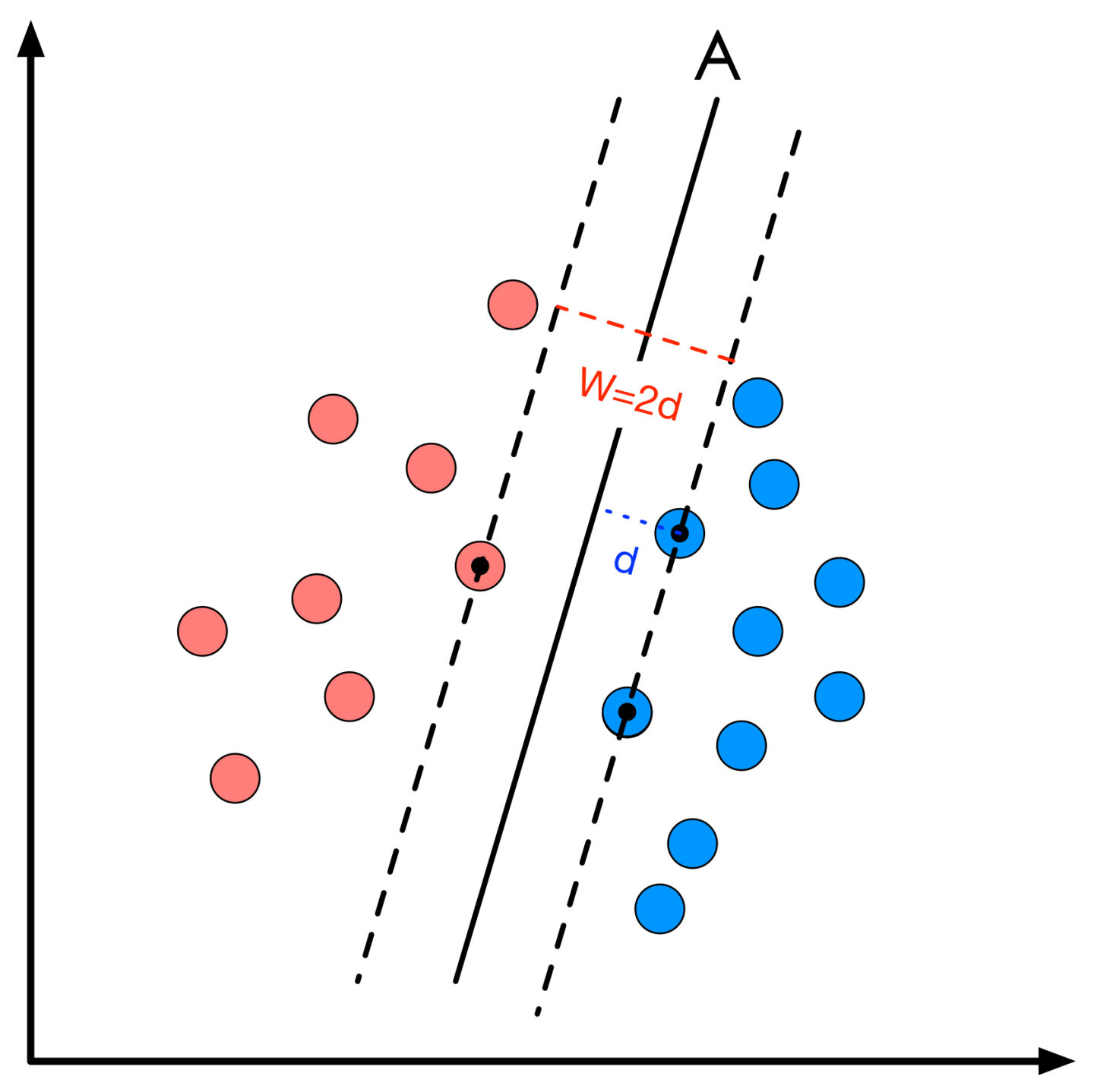
所以分类间隔计算似乎相当简单，无非就是点到直线的距离公式。

如果你想要回忆高中老师在黑板上推导的过程，可以随便在百度文库里搜索关键词“点到直线距离推导公式”，你会得到至少6、7种推导方法。但这里，请原谅我给出一个简单的公式如下：

这里是$||w||$向量$w$的模，表示在空间中向量的长度，$x=[x_1,x_2{]}^T$就是支持向量样本点的坐标。$w,r$就是决策面方程的参数。而追求$w$的最大化也就是寻找$d$的最大化。看起来我们已经找到了目标函数的数学形式。

但问题当然不会这么简单，我们还需要面对一连串令人头疼的麻烦。

2.3 约束条件

接着2.2节的结尾，我们讨论一下究竟还有哪些麻烦没有解决：

1）并不是所有的方向都存在能够实现100%正确分类的决策面，我们如何判断一条直线是否能够将所有的样本点都正确分类？

2）即便找到了正确的决策面方向，还要注意决策面的位置应该在间隔区域的中轴线上，所以用来确定决策面位置的截距$r$也不能自由的优化，而是受到决策面方向和样本点分布的约束。

3）即便取到了合适的方向和截距，公式(2.6)里面的$x$不是随随便便的一个样本点，而是支持向量对应的样本点。对于一个给定的决策面，我们该如何找到对应的支持向量？

以上三条麻烦的本质是“约束条件”，也就是说我们要优化的变量的取值范围受到了限制和约束。

事实上约束条件一直是最优化问题里最让人头疼的东西。但既然我们已经论证了这些约束条件确实存在，就不得不用数学语言对他们进行描述。尽管上面看起来是3条约束，但SVM算法通过一些巧妙的小技巧，将这三条约束条件融合在了一个不等式里面。

我们首先考虑一个决策面是否能够将所有的样本都正确分类的约束。

图2中的样本点分成两类（红色和蓝色），我们为每个样本点$x_i$加上一个类别标签$y_i$：

如果我们的决策面方程能够完全正确地对图2中的样本点进行分类，就会满足下面的公式

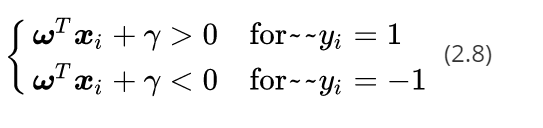
如果我们要求再高一点，假设决策面正好处于间隔区域的中轴线上，并且相应的支持向量对应的样本点到决策面的距离为d，那么公式(2.8)就可以进一步写成：

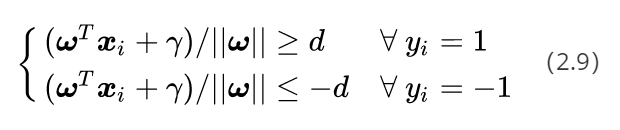
我们对公式(2.9)中的两个不等式的左右两边除上d，就可得到：

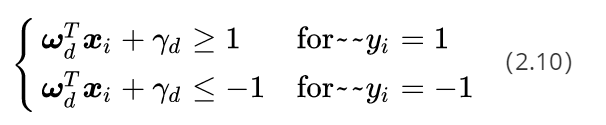
其中

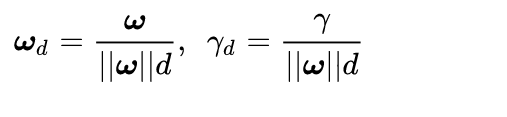
把$w_d$ 和$r_d$就当成一条直线的方向矢量和截距。

你会发现事情没有发生任何变化，因为直线$w_d^{T}x+r_d=0$和$w^T+r=0$直线其实是一条直线。

现在，现在让我忘记原来的直线方程参数$w$和$r$，我们可以把参数 $w_d$和$r_d$重新起个名字，就叫它们$w$和$r$。我们可以直接说：“对于存在分类间隔的两类样本点，我们一定可以找到一些决策面，使其对于所有的样本点均满足下面的条件：”

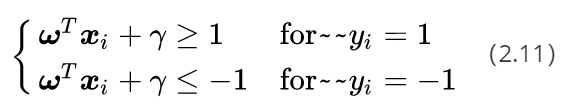
公式(2.11)可以认为是SVM优化问题的约束条件的基本描述。

2.4 线性SVM优化问题基本描述

公式(2.11)里面$w^T{x}_i+r=1or-1$的情况什么时候会发生呢？

参考一下公式(2.9)就会知道，只有当$x_i$是决策面$w^T{x}_i+r=0$所对应的支持向量样本点时，等于1或-1的情况才会出现。这一点给了我们另一个简化目标函数的启发。

回头看看公式(2.6)，你会发现等式右边分子部分的绝对值符号内部的表达式正好跟公式(2.11)中不等式左边的表达式完全一致，无论原来这些表达式是1或者-1，其绝对值都是1。所以对于这些支持向量样本点有：

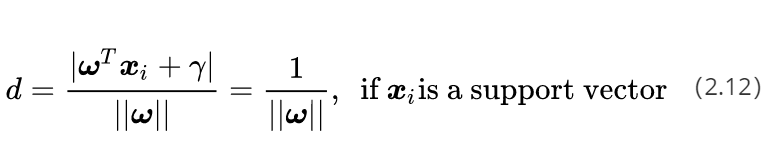
公式(2.12)的几何意义就是，支持向量样本点到决策面方程的距离就是$1/||w||$。

我们原来的任务是找到一组参数$w,r$使得分类间$w=2d$隔最大化，根据公式(2.12)就可以转变为$||w||$的最小化问题，也等效于$1/2||w|{|}^2$的最小化问题。我们之所以要在$||w||$上加上平方和1/2的系数，是为了以后进行最优化的过程中对目标函数求导时比较方便，但这绝不影响最优化问题最后的解。

另外我们还可以尝试将公式(2.11)给出的约束条件进一步在形式上精练，把类别标签和两个不等式左边相乘，形成统一的表述：

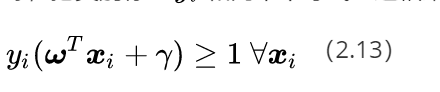
好了，到这里我们可以给出线性SVM最优化问题的数学描述了：

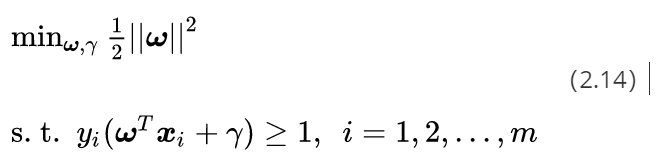
这里m是样本点的总个数，缩写s. t. 表示“Subject to”，是“服从某某条件”的意思。公式(2.14)描述的是一个典型的不等式约束条件下的二次型函数优化问题，同时也是支持向量机的基本数学模型。

3、总结

1、SVM目标函数的推导逻辑：

由基本的一元一次方程引出决策面方程，然后对于该决策面方程进行求解，实际上就是求 $w$和 $r$使$d$ 最大。

但是对于决策面方程有几个前提条件

一是这条线要划分所有样本点（满足2.11）
二是x是支持向量样本点 （即2.11取等于的情况下）

由这这个条件，建立巧妙联系有（即2.12）

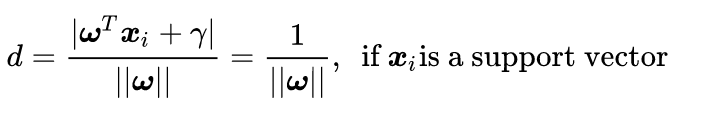
现在就由求 $w$和$r$ 使d最大，变成了让$||w||$最小，使d最大！

最后对式子进行精炼，就有（2.14）：

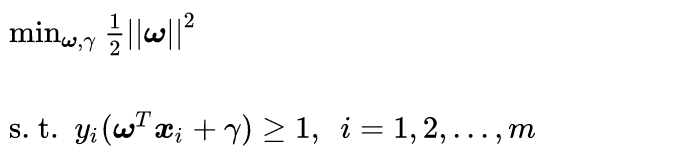
2、SVM目标函数求解逻辑：

基于拉格朗日乘子法的线性SVM优化问题模型