2. 图的深度优先遍历
问题:计算出最短行车方案。
下面是城市的地图:
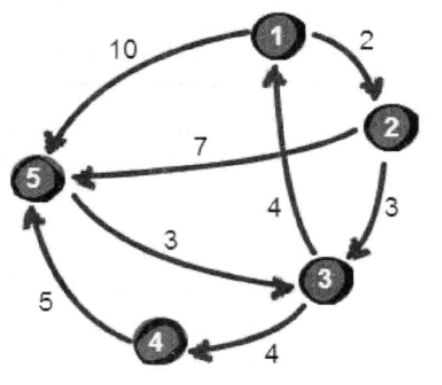
数据是这样给出的,如下:

第一行的5表示有5个城市(城市编号为1~5),8表示有8条公路。
接下来8行每行是-条类似“abc”这样的数据,表示有一条路可以从城市a到城市b,并且路程为c公里。
需要注意的是这里的公路都是单行的。
小哼家在1号城市,小哈家在5号城市。
现在请求出1号城市到5号城市的最短路程(也叫做最短路径)。
已知有5个城市和8条公路,可以用一个5*5的矩阵(二维数组e)来存储这些信息,如下:
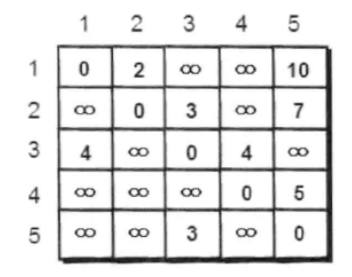
上面这个二维矩阵表示了任意两个城市之间的路程。
比如e[1][2]的值为2就表示从1号城市到2号城市的路程为2公里。
∞ 表示无法到达。另外,此处约定一个城市自己到自己的距离是0。
接下来寻找从1号城市到5号城市的最短路程(最短路径)了。
首先从1号城市出发,可以看出1号城市可以到2号城市和5号城市。
那此时是先到2号城市呢,还是先到5号城市呢?
这里需要规定个顺序,比如按照从1到n的顺序。
现在先选择到2号城市,可以看出从2号城市可以到3号城市和5号城市。
按照刚才规定好的顺序,先到3号城市。
同理,3号城市又可以到4号城市,4号城市可以到5号城市(5号城市为最终目标城市),此时就已经找出了一条从1号城市到5号城市的路径,这条路径是
1→2→3→4→5,路径的长度是14。
因为这条路径的长度并不一定是最短的。因此还需要再返回到4号城市看看还有没有别的路可以让路径更短一点。
但是发现4号城市除了可以到5号城市,便没有别的路可以走了。此时需要返回到3号城市。
发现3号城市除了一条路通往4号城市也没有其他的路了,此时又继续回到2号城市。
发现2号城市还有一条路可以到5号城市,于是就产生了1→2→5这条路径,路径长度为9。
在对2号城市的所有路都尝试过后,又返回到了1号城市。发现1号城市还有一条路是通向5号城市的,于是又产生了一条路径1→5,路径长度为10。
至此,已经找出了所有从1号城市到5号城市的通路,一共有3条,分别是:

可以用一个全局变量min来更新每次找到的路径的最小值,最终找到的最短路径为9。
此外,还需要一个book数组来记录哪些城市已经走过,以免出现1→2→3→1这样的无限死循环。代码如下:
#include <stdio.h>
min = 99999999, book[101], n, e[101][101];//假设999999999为正无穷
//cur是当前所在的城市编号, dis是当前已经走过的路程
void dfs(int cur, int dis) {
int j;
if (dis > min) return;//如果当前走过的路程已经大于之前找到的最短路,则没有必要再往下尝试了,立即返回
if (cur == n) //判断是否到达了目标城市
{
if (dis < min) {
min = dis;//更新最小值
}
return;
}
for (j=1; j<=n; j++) //从1号城市到n号城市依次尝试
{
//判断当前城市cur到城市j是否有路,并判断城市j是否在已走过的路径中
if (e[cur][j]!=99999999 && book[j]==0)
{
book[j] = 1;//标记城市j已经在路径中
dfs(j, dis+e[cur][j]);//从城市j再出发,继续寻找目标城市
book[j] = 0;//之前一步探索完毕之后,取消对城市j的标记
}
}
return;
}
int main() {
int i, j, m, a, b, c;
scanf("%d %d", &n, &m);
//初始化二维矩阵
for (i=1; i<=n; i++) {
for (j=1; j<=m; j++) {
if (i==j) {
e[i][j] = 0;
} else {
e[i][j] = 99999999;
}
}
}
//读入城市之间的道路
for (i=1; i<=m; i++) {
scanf("%d %d %d", &a, &b, &c);
e[a][b] = c;
}
//从1号城市出发
book[1] = 1;//标记1号城市已经在路径中
dfs(1, 0);//1表示当前所在的城市编号,0表示当前已经走过的路程
printf("%d\n", min);//打印1号城市到5号城市的最短路径
getchar();getchar();
return 0;
}
数据验证:
5 8
1 2 2
1 5 10
2 3 3
2 5 7
3 1 4
3 4 4
4 5 5
5 3 3
返回值:
9
小结一下图的基本概念:
图就是有个顶点和M条边组成的集合。
这里的城市地图其实就是一个图,图中每个城市就是一个顶点,而两个城市之间的公路则是两个顶点的边。
图分为有向图和无向图,如果给图的每条边规定一个方向,那么得到的图称为有向图,其边也称为有向边。
在有向图中,与一个点相关联的边有出边和入边之分,而与一个有向边关联的两个点也有始点和终点之分。
相反,边没有方向的图称为无向图。
处理无向图和处理有向图的代码几乎是一模一样的。只是在处理无向图初始化的时候有-点需要注意。
“abc”表示城市a和城市b可以互相到达,路程为c公里。
因此需要将e[1][2]和e[2][1]都初始化2,因为这条路是双行道。初始化后的数组e如下:
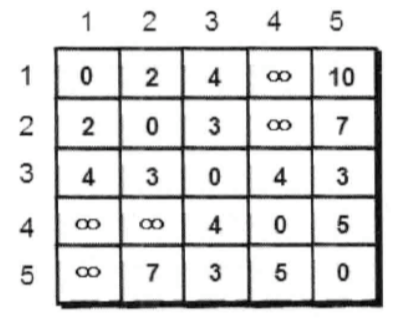
这个表是对称的(上一节我们已经说过),这是无向图的一个特征。
在这个无向图中,会发现从1号城市到5号城市的最短路径不再是1→2→5,而是1→3→5,路径长度为7。
参考
《啊哈!算法》 —— 第5章 图的遍历