3. 图的广度优先遍历
问题:
小哼和小哈一同坐飞机去旅游,他们现在位于1号城市,目标是5号城市,可是1号城市并没有到5号城市的直航。
不过小哼已经收集了很多航班的信息,现在小哼希望找到一种乘坐方式,使得转机的次数最少,如何解决呢?
验证数据:
5 7 1 5
1 2
1 3
2 3
2 4
3 4
3 5
4 5
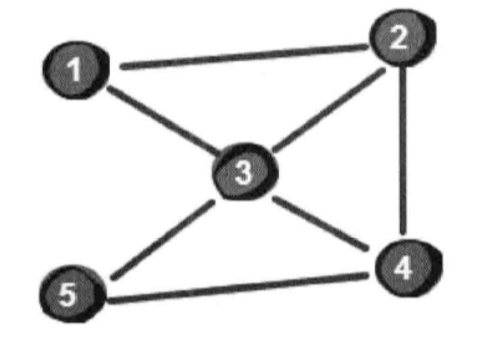
第一行的5表示有5个城市(城市编号为1~5),7表示有7条航线,1表示起点城市,5表示目标城市。
接下来7行,每行是一条类似“ab”这样的数据表示城市a和城市b之间有航线,也就是说城市a和城市b之间可以相互到达。
还是使用邻接矩阵来存储图,需要注意的是这里是无向图。
城市的编号就是图的顶点,而航班则是两顶点之间的边。
小哼要求的是转机次数最少,所以可以认为所有边的长度都是1。
下面用广度优先搜索来解决这个问题。
首先将1号城市入队,通过1号城市可以到达(扩展出)2号和3号城市。
2号城市又可以扩展出3号城市和4号城市。
因为3号城市已经在队列中,所以只需将4号城市入队。
接下来3号城市又可以扩展出4号城市和5号城市,因为4号城市也已经在队列中,所以只需将5号城市入队。
此时已经找到了目标城市5号城市,算法结束。
完整代码如下:
#include <stdio.h>
struct note
{
int x;//城市编号
int s;//转机次数
};
int main() {
struct note que[2501];
int e[51][51] = {
0}, book[51] = {
0};
int head, tail;
int i, j, n, m, a, b, cur, start, end, flag=0;
scanf("%d %d %d %d", &n, &m, &start, &end);
//初始化二维矩阵
for (i=1; i<=n; i++) {
for (j=1; j<=n; j++) {
if (i==j) {
e[i][j] = 0;
} else {
e[i][j] = 99999999;
}
}
}
//读入城市之间的航班
for (i=1; i<=m; i++) {
scanf("%d %d", &a, &b);
//注意这里是无向图
e[a][b] = 1;
e[b][a] = 1;
}
//队列初始化
head = 1;
tail = 1;
//从start号城市出发, 将start号城市加入队列
que[tail].x = start;
que[tail].s = 0;
tail++;
book[1] = start;//标记start号城市已在队列中
//当队列不为空的时候循环
while (head < tail) {
cur = que[head].x;//当前队列中首城市的编号
for (j=1; j<=n; j++) //从1-n依次尝试
{
//从城市cur到城市j是否有航班并且判断城市j是否已经在队列中
if (e[cur][j] != 99999999 && book[j]==0) {
//如果从城市cur到城市j有航班并且城市j不在队列中, 则将j号城市入队
que[tail].x = j;
que[tail].s = que[head].s+1;
tail++;
//标记城市j已经在队列中
book[j] = 1;
}
//如果到达目标城市,停止扩展,任务结束,退出循环
if (que[tail].x == end) {
flag = 1;
break;
}
}
if (flag==1) {
break;
}
head++;//注意这地方,千万不要忘记当一个点扩展结束后, head++才能继续扩展
}
//打印队列中末尾最后一个(目标城市)的转机次数
//注意tail是指向队列队尾(即最后一位) 的下一个位置, 所以这需要-1
printf("%d\n", que[tail-1].s);
getchar();getchar();
return 0;
}
验证数据:
5 7 1 5
1 2
1 3
2 3
2 4
3 4
3 5
4 5
返回值:
2
当然也可以使用深度优先搜索解决,但是这里用广度优先搜索会更快。
广度优先搜索更加适用于所有边的权值相同的情况。
参考
《啊哈!算法》 —— 第5章 图的遍历