问题简述.
考虑n个元素[X …X ]的一个排列,若其中每一个元素X (1≤i≤n)都不在其原本的位置上,那么我们称这样的排列为原排列的错排,也称为更列(derangement),而我们关心原排列[X …X ]的错排,或者说更列的数量。通俗一点的问题版本就是,将n封信投入n个信箱,每一封信都投错的情况有多少种;以及n个人互相写贺卡,每个人都不写给自己,最终的贺卡发放情况有多少种?
递推公式.
n个元素对应于它们的n个位置,其更列个数记为D(n),那么D(i)就表示i个元素的更列个数。
- 放置第1个元素在位置【k】上,有n–1种选择,因为位置【1】不能使用;
- 放置第k个元素,若第k个元素放置在位置【1】上,则剩余的n–2个元素对应于它们原本的n–2个位置,有D(n–2)个更列;否则k放置于非1位置上,则将位置【1】视为新的位置【k】,考虑除了第一个元素以外的n–1个元素,它们有D(n–1)个更列,所以D(n)=(n–1)[D(n–1)+D(n–2)];
- 对于n=1和n=2的情况,D(n)分别为0和1是显然的。
出于计算方便,我们令D(x)=x!N(x),其中1≤x≤n,N(x)是一个小于1的数(更列数不可能超过全排列数),对于x=1和x=2的情况,N(x)分别为0和0.5是显然的。所以根据上面得到的递推公式以及D(x)=x!N(x),我们有如下的推导过程:
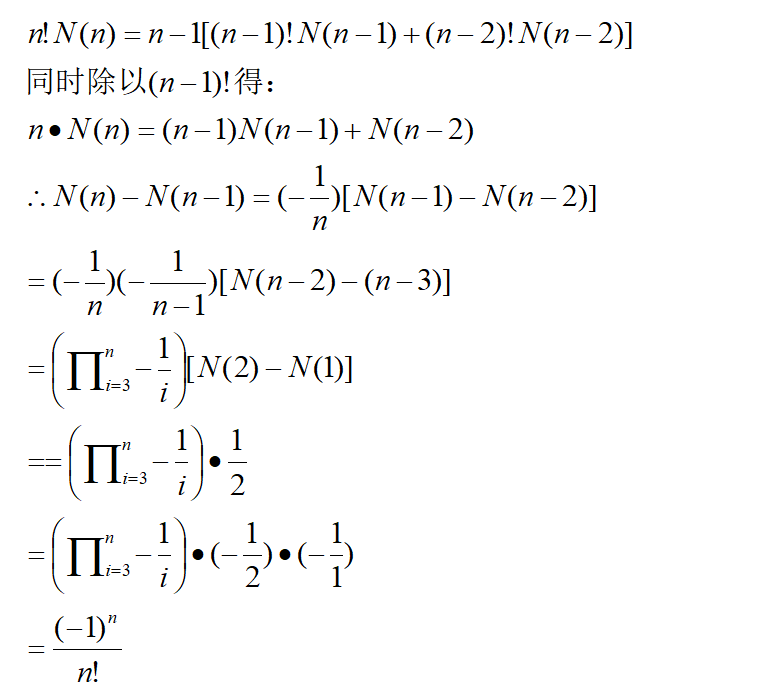

容斥原理.
在计数时,必须注意没有重复,没有遗漏。为了使重叠部分不被重复计算,人们研究出一种新的计数方法,这种方法的基本思想是:先不考虑重叠的情况,把包含于某内容中的所有对象的数目先计算出来,然后再把计数时重复计算的数目排斥出去,使得计算的结果既无遗漏又无重复,这种计数的方法称为容斥原理。
n个元素的排列有n!种,其中第r个元素还在位置【r】的情况有(n–1)!种,所以我们需要减去n*(n–1)!,但其中将r和s两个元素分别还在位置【r】和位置【s】的情况多减去了一次,所以还需要加上n*(n-1)*(n-2)!/2,但其中又将r、s和t三个元素分别还在原地的情况多加了一次。也就是说,n个元素的全排列中,减去1个元素不错排的情况后,发现多减了一次2个元素不错排的情况,所以需要加上;加上后又发现多加了一次3个元素不错排的情况,又需要减去;减去后又发现…所以,最后我们得到如下的过程:
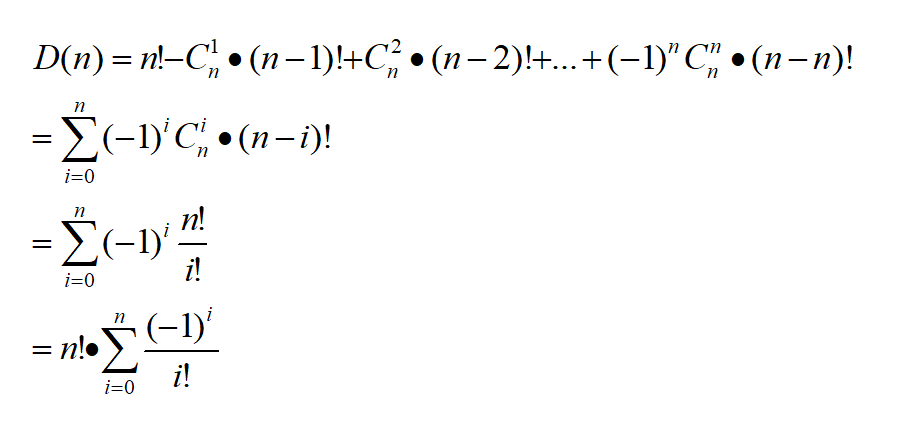
二项式反演.
令f(x)为x个元素的全排列数,g(y)为y个数都不在它们自己位置上的排列数所以我们有以下等式:
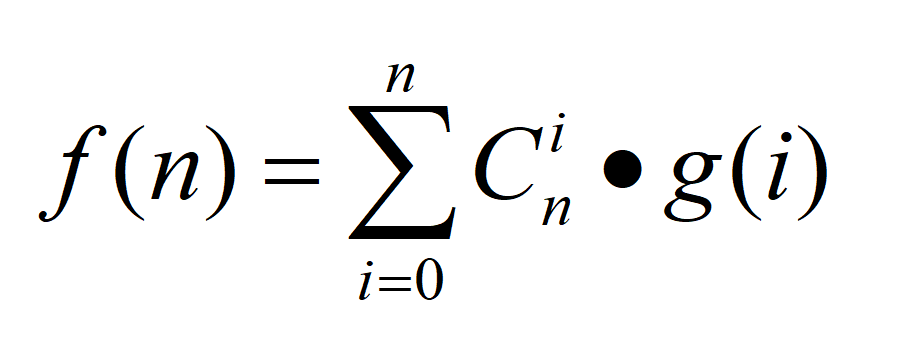
根据二项式反演,我们可以得到:
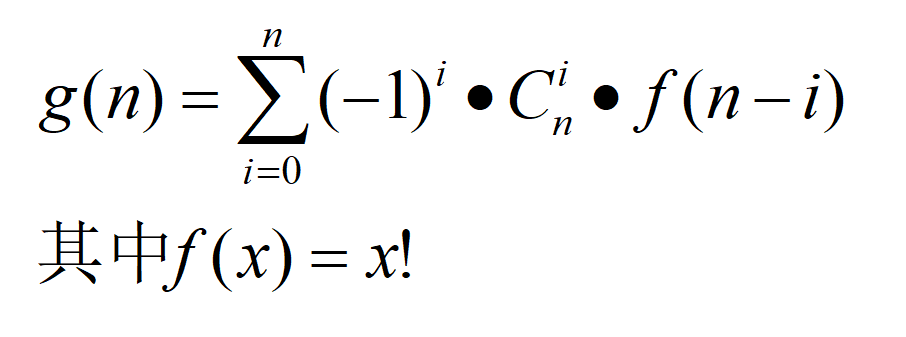
进一步化简可以得到与上面两种方法相同的结果。
错排公式近似式.
根据前面的推导,我们得到如下公式:
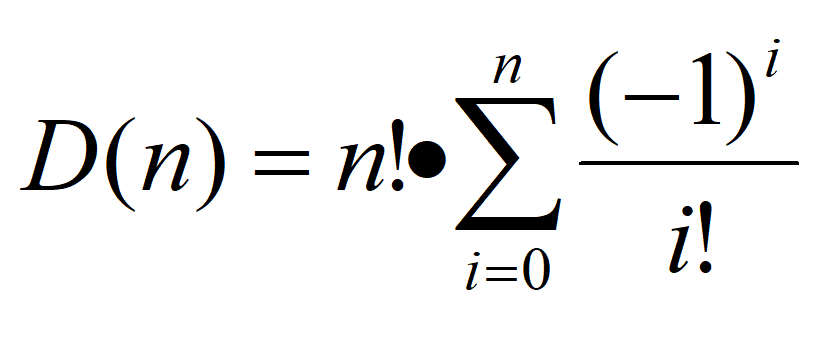
不难发现,由于求和项的存在,n很大时由该公式计算D(n)相当困难,所以我们在实际计算时可以使用下列近似式:

关于近似式的正确性证明如下:
