【微积分的本质|笔记】指数函数求导

微积分的本质

---

P5 指数函数求导

• 本节从指数函数的实际意义出发，通过代数运算，推导出指数函数的一般性质
• 从而引出e的定义，理解所谓“指数函数”的形式的可行性，以及神秘的常数。

#1 从实际角度看f(x) = 2^x

1. 把2^t这个函数看成是随着时间t按照比例增长的人口数量
   

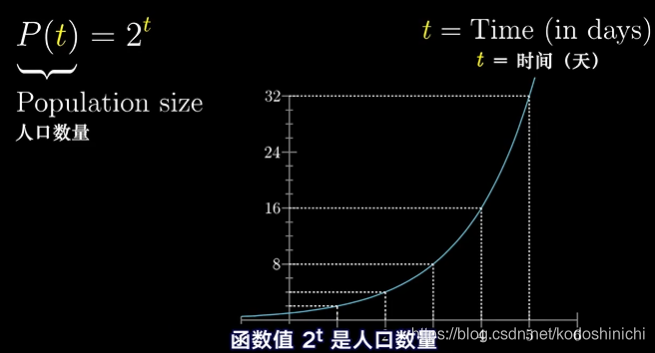
p.s. 这里如果把2^t看成是人口数量，那么函数整个还是比较离散的概念。为了后续按照导数的定义，使得微小变化量有实际意义，往往也会采取将函数值看成是人口总重量。

2. 定性求解dM/dt（也就是人口重量的微小变化量除以时间的微小变化量）

①先来考虑单天的微小变化量的比值

如下图，考虑从第三天到第四天的微小变化。第三天人口总重为2³=8，第四天人口总重为2⁴=16，所以dM=8，而dt=1.

总的来说，多进行几次推导计算（比如从第四天到第五天，增长了16，第五天到第六天增长了32…），不难发现：每天的增长率就等于当天开始时π酱的数量。

于是，做出一个合理猜想——2^t的导数等于该函数本身。

猜想的不合理性：虽然整个趋势预测的并没有错，但是所谓导数的定义，是要在有限小的一个变化趋势中去看比值，比如说1/10,1/100,1/1000这样的微小量。

3. 定量求解dM/dt
   
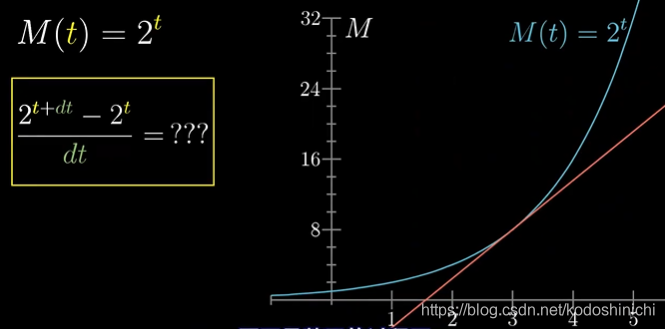
   ①微小量比值式的转换

将2^t+dt拆解成2^t*2^dt；这个变换可以说是指数函数最重要的性质之一，将加法的思想（微小量）转换成乘法的思想（变化率和比率）

②提取公因式，将微小量比值式转换成两个分部相乘的形式。

这一步转换看起来似乎比较平常，也是顺应变化趋势的，但是其实蕴含着一个很重要的思想。
它将右边式子（关于dt求极限）变得与具体的时间t无关了，所有与确切时间t相关的因子都放在在式子的左边。

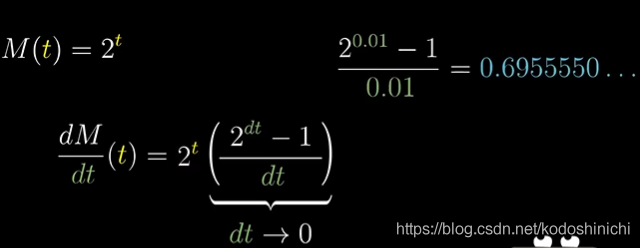
而关于右边这个式子的取值，虽然笔记还没有做到极限的内容，但是根据极限的思想和定义，我们都可以知道，右部最终是趋于一个常数的。

③得到最终的导数表达式

4. 形如y = a^x的导数的一般式子

形如这样的函数（也即指数函数）的导数都等于自身的一定常数倍。

而常数的取值和a底数的数值有关。

#2 指数函数y=e^x的重要性

引出e的原因？
——根据前文，我们知道a^x的导数就等于其自身乘上某一常数，我们好奇是否存在某个底数a使得函数a^x的导数就等于其自身，也就是常数为1.

1. e的定义

• e^x这样的指数函数，就满足我们的要求——其导数等于自身。
• 为什么呢？
  ——因为自然指数e就是这样的定义而来的。
  

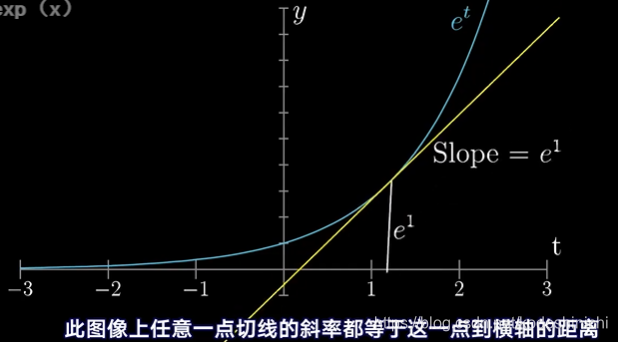
2. y=e^x图像的理解

性质：该图像上任意一点的切线的斜率都等于这一点到横轴的距离。

3. y=a^x导数式中常数的含义

①指数复合函数的链式求导法则

f(x) = e^cx^ f'(x) = ce^cx^

②以2^x为例来理解导数中常数的意义

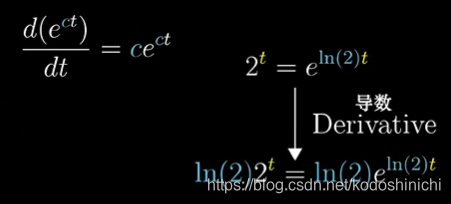
按照对数的定义可知2可以写成e^ln2
那么可以把一个一般的指数函数2^x写成一个自然常数为底的复合指数函数

从而根据链式法则，推导出——
y=a^x的导数中的常数为lna

#3 形如y=e^ct的指数函数

指数函数有很多可行的表达方式。

在日常生活或是实际应用中，我们往往会采取将指数函数写成y=e^ct的形式，因为这样c这个常数的意义可以一目了然。

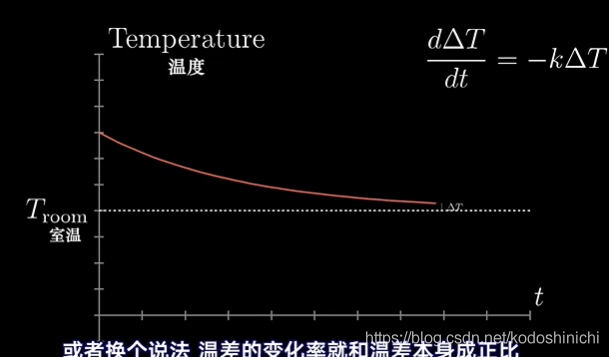
1. 在许多自然现象里，变化率都和变化量成正比

因此——可以建模成指数函数进行求解

---

后记

本文为观察《微积分的本质》B站公开课所做，如果问题欢迎评论或私信交流。

原视频链接

【官方双语/合集】微积分的本质 - 系列合集