微积分的本质（六）：多元微积分入门——隐函数求导

版权声明：本文为博主原创文章，如需转载，请注明出处： https://blog.csdn.net/MASILEJFOAISEGJIAE/article/details/82930268

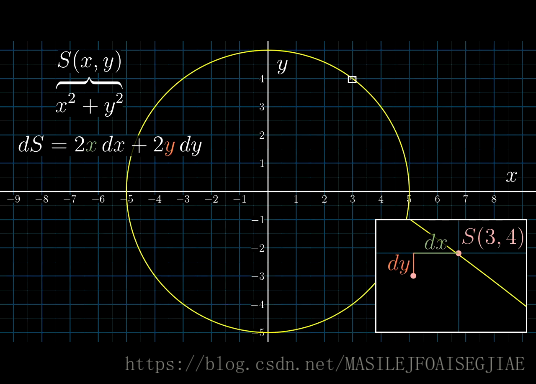
例1.表达式 $S$表示一个圆心在原点，半径为5的圆，其隐函数如下：
$S(x,y)=x^2+y^2 = 25$

对表达式 $S$求导，要考虑 $S$的两个变量 $x,y$同时发生的变化，既有 $x$的微小变化量 $dx$，也有 $y$的微小变化量 $dy$。无论这个变化是否在某个圆上，都会在 $xy$平面上往某种方向移动了微小的一步。

对 $S$求导，则有
$dS=2xdx+2ydy=0$
几何意义：对 $S$求导，就是在求这次移动所导致的 $S$的变化量 $dS$是多少，即 $x^2+y^2$的值相应变化了多少。对于求导而言，虽然是个近似值，但是这个近似值会随着 $dx,dy$越来越小而越来越精确。

重点在于，当把每一次移动都落在圆上的时候，就相当于维持 $S$的值不变，则 $S$的变化量 $dS$就应该为0（严格意义上来讲，这样约束会使得每一步落在圆的一条切线上，但迈的步子足够小的话，可以近似等同于落在圆上）。

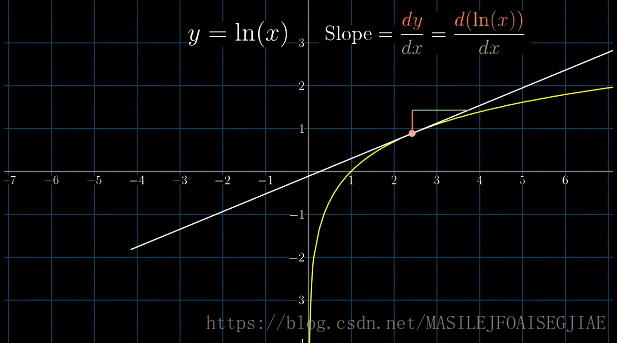
例2.已知的 $f(x)=e^x$的导函数为其本身，即 $\frac{d(e^x)}{dx}=e^x$，求其反函数 $f(x)=\ln(x)$的导函数

将 $\ln(x)$的图像想象成一个隐函数曲线，该曲线表示 $xy$平面上满足等式 $y=\ln(x)$的所有点 $(x,y)$的集合。

函数图像的切线的斜率 $\frac{dy}{dx}$就是 $\ln(x)$的导函数。

其中，
$y=\ln(x)$ 等价于 $e^y=x$
对等式两边同时求导有
$e^ydy=dx$
几何意义：从图像上移动微小的一步 $(dx,dy)$，对等式的两边有什么影响。要让这一步依然落在曲线上，等式左边的变化量 $e^ydy$ 必须等于等式右边的变化量 $dx$。
则 $\ln(x)$的导函数为
$\frac{dy}{dx}=\frac{1}{e^y}=\frac{1}{x}$

从本例子可以看出，隐函数求导的一个作用是可以利用从已有的导函数，推导出别的函数的导函数。