用Python学《微积分B》（多元函数的微分）

  多元函数的微分包括“偏导数”和“全微分”，而“全微分”在满足一定条件时，通过“偏导数”的叠加来表示。这种叠加可以让人联想到“空间向量”与“直角坐标系”的各个分量之间的叠加。
  偏导数（Partial Derivative）内容相对简单，主要包括：偏导数与全微分（全导数-total derivative）的关系、多元函数偏导数与一元函数的导数的关系、偏导数的标记法、偏导数的几何意义、高阶偏导数、混合偏导数。此外，math is fun也对“Partial Derivatives”有形象的介绍。
  全微分（Total Derivative）部分主要关注全微分与偏导数的关系。整个多元函数的微分是循着以下思路展开的：
  一元函数导数 $\; \leftarrow$切片$\leftarrow \;$ 多元函数偏导数 $\; \rightarrow$叠加$\rightarrow \;$多元函数全微分。
  很明显，它应用了两种方法：切片（降维）和叠加（分解）。

一、偏导数

1，多元函数的偏导数与一元函数导数
  回顾一下一元函数导数的定义

$$f'(x_0) = \lim_{x \to x_0}\frac{f(x)-f(x_0)}{x-x_0}$$
  它是用“极限”来表示的，描述函数 f(x) 在 $x_0$ 点附近（邻域）函数的变化量与自变量的变化量的关系，因此也记作 $\frac{\mathrm{d}f(x)}{\mathrm{d}x}$。比如圆的面积与半径的变化关系可以表示为：
$$\frac{\mathrm{d}S_C(r)}{\mathrm{d}r} = \frac{\mathrm{d}[\pi r^2]}{\mathrm{d}r}$$
  类似地，多元函数的导数也是描述 在某点附近（ $P_0$ 的邻域）函数的变化量与自变量的变化量的关系。同样地，它也需要用“极限”来表示，但是，我们在上一节学到，多元函数在某点的极限有不同的逼近路径，且沿不同的逼近路径求得的极限值是有可能不同的。因此，多元函数的导数（全导数-total derivative）是比较复杂的。那么，我们考虑其中一种简单的情况，我们只考虑多元函数的函数值与其中一个变量的变化情况，而保持其他变量恒定，将多元问题转化为一元问题。比如：长方形的面积 $S = length * width$ ，这个面积随两个变量变化。如果我们将其中一个变量固定，比如固定宽度，那么，这个长方形的面积 $S = W_0 * x$，即这个面积与长度呈线性增长关系。
$$\frac{\partial S_R(l, w_0)}{\partial l} = \frac{\partial [w_0 * l]}{\partial l} = w_0$$
  这就是“多元函数的偏导数”，很明显，它将“多元函数问题”转化为了“一元函数问题”。用极限可以表示为：
$$f_x(x_0,y_0)= \lim_{\Delta x \to 0}\frac{f(x_0+\Delta x, y_0)-f(x_0,y_0)}{\Delta x}$$
注：从某种意义上来说，多元函数偏导数就是一元函数导数。但是，它们在数学表达式上是有很大的区别的：
1）一元函数导数 $\frac{\mathrm{d}f(x)}{\mathrm{d}x}$ ，可以当作分式。比如 “链导法”
$$\frac{\mathrm{d}f[u(x)]}{\mathrm{d}x} = \frac{\mathrm{d}f(u)}{\mathrm{d}u} \cdot \frac{\mathrm{d}u(x)}{\mathrm{d}x}$$
2）多元函数偏导数不能当作分式，比如： $z = xy$
$$\frac{\partial z}{\partial x} = y, \; x = \frac{z}{y} \Rightarrow \frac{\partial x}{\partial y} = -\frac{z}{y^2}, \;y = \frac{z}{x} \Rightarrow \frac{\partial y}{\partial z} = \frac{1}{x} \\ \Rightarrow \frac{\partial z}{\partial x} \cdot \frac{\partial x}{\partial y} \cdot \frac{\partial y}{\partial z}= -\frac{ z}{xy} = -1$$
  矛盾！！！
2，偏导数的几何意义
1）一元函数导数的几何意义
  一元函数可以看作平面上的一条曲线，它在某点的导数就是这条曲线在某点的切线的斜率，如下图：

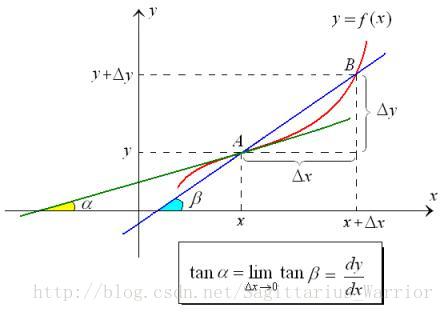
2）二元函数偏导数
  将二元函数看作是空间曲面 $F(x,y,z) = 0$ ，也可以写作 $z = f(x,y)$ 。那么，二元函数对 x 的偏导数相当于先做一个 $y = y_0$ 的平面，该平面与空间曲面相交，这个“交线”肯定位于平面 $y = y_0$ 内，换句话说，这个“校线”是一个一元函数 $z = \varphi(x)$ 。
  偏导数 $\frac{\partial f(x,y_0)}{\partial x}$ 就是指这条 “交线” 上一点 $(x_0,y_0)$ 的切线的斜率。如下图：

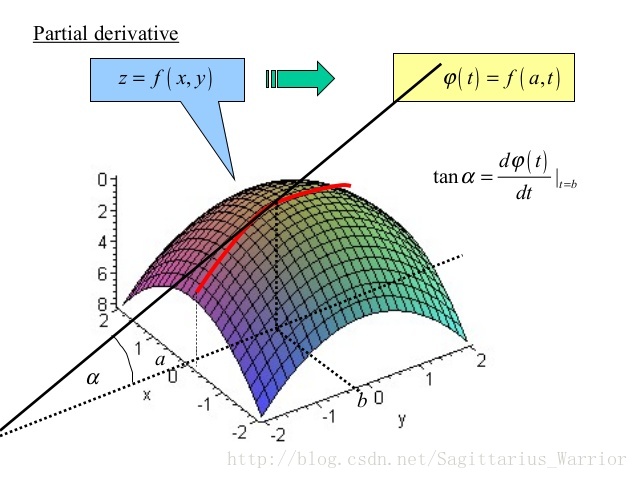
注：对于空间曲面应用的是“切片”，对于空间曲线一般应用“投影”，需要注意二者的区别。
3，高阶偏导数和混合偏导数
  参照一元函数的高阶导数，多元函数的偏导数同样也可以多次求导，即高阶偏导数。需要注意的是混合偏导数

$$\frac{\partial z^2}{\partial x \partial y} \;,\; \frac{\partial z^2}{\partial y \partial x}$$
  这两个偏导数是不一样的，其中有一个定理：如果它们在区域D内都连续，那么这两个值相等。即“在偏导数连续的情况下，混合偏导数与求导的顺序无关”。

二、课后习题

  Sympy对偏导数支持的非常好，下面直接用课后习题来演示：

$$z = sin(xy), \; \frac{\partial z^3}{\partial x \partial y^2} = ?$$

#Exercise 10-2-1-4
from sympy import *
init_printing()
x,y = symbols('x y')
f,g = symbols('f g', cls=Function)
f = sin(x * y)
f, f.diff(x, y, y)

$$\left ( \sin{\left (x y \right )}, \quad - x \left(x y \cos{\left (x y \right )} + 2 \sin{\left (x y \right )}\right)\right )$$

三、全微分

注：为了简单起见，我们只说二元函数的全微分。
1，全微分的定义
  偏导数研究的是函数值的变化量与x轴分量或y轴分量变化量的比值，从“空间向量”的角度来看，如果将这两个分量上的变化进行某种“叠加”，有没有可能得到“向量”在任一方向变化的规律？
  答案肯定的，这就是全微分，它在数学上是用“偏导数的叠加”来表示的。
1）全增量

$$\Delta z = f(x+\Delta x, y + \Delta y) - f(x,y) = A\Delta x + B\Delta y + o(\rho)$$
其中，$\rho = \sqrt{(\Delta x)^2 + (\Delta y)^2}$ ，正好是两点间距离的公式。
注：原课程中在引入 $\rho$ 时，用到了“无穷小的比较”
2）全微分
$$\mathrm{d} z = A\Delta x + B\Delta y$$
  类似一元微分与增量的关系，多元微分同样是增量的线性部分。
3）几何意义
  一元微分在几何上表示为在平面上上某点附近用切线近似平面曲线，类似地，二元全微分在几何上表示在某点附近用切面近似空间曲面。换一个角度来看这个“切面”，它实际上是两条相交的直线（切线）确定的一个平面。
2，必要条件
  可微（differentiable） $\Rightarrow$ 偏导数存在，且
$$\mathrm{d} z = \frac{\partial z}{\partial x}\Delta x + \frac{\partial z}{\partial y}\Delta y$$
3，充分条件
  偏导数存在且连续 $\Rightarrow$ 可微
注：通常把二元函数的全微分等于它的两个偏微分之和这件事称为二元函数的微分复合“叠加原理”。
4，充要条件
$$\Delta f(a,b) = \frac{\partial f(a,b)}{\partial x}\Delta x + \frac{\partial f(a,b)}{\partial y}\Delta y + \epsilon_1 \Delta x + \epsilon_2 \Delta y$$
其中，
$$\lim_{\Delta x \to 0, \Delta y \to 0}\epsilon_1=0 \;, \; \lim_{\Delta x \to 0, \Delta y \to 0}\epsilon_2=0$$
5，可微与偏导数的关系

全微分计算

  全微分的计算一般都可以转化为偏导数的计算，此外，可以利用全微分进行一些近似计算。下面以课后练习为例，进行演示。
Exercise 10-3-1-1

$$z = arctan \; \frac{x+y}{x-y} \; ,\; \mathrm{d}z = ?$$

#Exercise 10-3-1-1
from sympy import *
init_printing()
x,y = symbols('x y')
f,g = symbols('f g', cls=Function)
f = atan((x+y)/(x-y))
f, simplify(f.diff(x)),simplify(f.diff(y))

$$\left ( \operatorname{atan}{\left (\frac{x + y}{x - y} \right )}, \quad - \frac{y}{x^{2} + y^{2}}, \quad \frac{x}{x^{2} + y^{2}}\right )$$


Exercise 10-3-2
$$(1.04)^{2.02} \approx ? \\ \sqrt{(1.02)^3+(1.97)^3} \approx ?$$
提示：第一式可以抽象为
$$z = f(x,y) = x^y$$
第二式可以抽象为
$$z = f(x,y) = \sqrt{x^3+y^3}$$
根据下式估算
$$\Delta f(a,b) = \frac{\partial f(a,b)}{\partial x}\Delta x + \frac{\partial f(a,b)}{\partial y}\Delta y + \epsilon_1 \Delta x + \epsilon_2 \Delta y$$
$$f(x+\Delta x, y + \Delta y) \approx f(x,y) + \frac{\partial f(x,y)}{\partial x}\Delta x + \frac{\partial f(x,y)}{\partial y}\Delta y$$
解：
$$(1.04)^{2.02} \approx 1^2 + 1^{2-1} \cdot 2 \cdot (0.04) + 1^2 \cdot log(1) \cdot (0.02) = 1.08$$
$$\sqrt{(1.02)^3+(1.97)^3} \approx \sqrt{1^3+2^3} + \frac{3 \cdot 1^2}{2 \cdot \sqrt{1^3+2^3}} \cdot (0.02)+ \frac{3 \cdot 2^2}{2 \cdot \sqrt{1^3+2^3}} \cdot (-0.03) = 2.95$$