用Python学《微积分B》（多元函数的极限）

  先回顾一下“一元微分学”部分的知识链：数轴 -> 数列 -> 数列的收敛 -> （不等式）数列的极限 -> 一元函数的极限 -> 一元函数的连续性 -> 一致连续 -> 导数 -> 微分。
  从上面的链条可以看出：数列是一维空间（数轴）的、离散的研究对象；而函数二维空间（平面）的、连续的研究对象。而多元函数微积分（Multivarialbe Calculus）是对之前“一元微分学”的维度扩展。

一、点列

1，从“数列”（sequence）到“点列”（point range）
  从几何角度来看，数列是分布在数轴上的点，而点列是分布在平面或空间中的点。它们之间的主要差异是维度不一样，也可以将数列看作一维的点列。
1）数列中两个元素的距离

$$dis(a,b) = |b - a| = |x_2 - x_1|,\; \; \;\;\;\; a,b \in R$$
2）二维点列（平面）中两点的距离
$$dis(\vec{A},\vec{B}) = |\vec{B} - \vec{A}| = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2},\;\;\;\;\;\; \vec{A},\vec{B} \in R^2$$
3）三维点列中两点的距离
$$dis(\vec{A},\vec{B}) = |\vec{B} - \vec{A}| = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2 + (z_2-z_1)^2},\;\;\;\;\;\; \vec{A},\vec{B} \in R^3$$
  依次类推，可以扩展到n维点列，都可以将它们转换为n维向量的运算。
2，点列的收敛
  数列收敛的定义是
$$\lim_{n \to \infty} |a_n - A| = 0$$
注：上式的绝对值可以去掉，极限的定义本身就是用绝对值不等式来描述的。
   $R^n$ 中点列收敛的定义是借助 distance 来表示的（P - point）
$$\lim_{m \to \infty} dis(P^m, P^0) = 0$$
  从向量的角度来说，上式等价于
$$\lim_{m \to \infty} |P_k^m - P_k^0| = 0$$
  即向量的各分量之差趋于零。

二、平面点集和n维空间

1，平面点集
  在平面直角坐标系中，任意一点 $P(x,y)$ ，包含来两个坐标值。换句话说，它是一个二元组（tuple）—— (x,y)。用集合的概念来表示平面点集如下：

$$E = \{(x,y)|(x,y)具有性质P\}$$
例如：中心在原点，半径为 r 的圆内的所有点，可以表示为：
$$C = \{(x,y)|x^2+y^2 < r^2 \}$$
或者
$$C=\{P| \;|OP| < r \}$$
2，邻域
$$U(P_0, \delta) = \{(x,y) \; | \; \sqrt{(x-x_0)^2 + (y-y_0)^2} < \delta \}$$
注：很明显，上式使用距离（distance）来描述的
  去心邻域
$$\dot{U}(P_0, \delta) = \{P \; | \; 0 < |PP_0| < \delta \}$$
3，内点、外点、边界点
  利用邻域可以很方便的描述点与点集的关系，常见的有：内点、外点和边界点（ $\partial E$ ）。
4，聚点
  如果对于任意给定的 $\delta > 0$ ，点P的去心邻域 $\dot{U}(P_0, \delta)$ 内总有 E 中的点，则称P是E的聚点。
5，开集、闭集
  主要看 $\partial E$ 与 E 的关系
6，连通集、区域（连通的开集）、闭区域
  区域 .vs 区间
7，有界集与无界集
注：本节的概念较多，准确定义可以去看教科书。
8，n维空间 —— $R^n$
  数轴到平面再到三维空间，依此类推，可以知道 $R^n$ 实际上是由 n 元组或n维向量来描述。

三、多元函数

1，多元函数（multi-variable function）的概念
  顾名思义，它是有多个自变量的函数，比如：圆柱体体积 $V = \pi r^2h$ ，它与柱面的半径和柱体的高都相关。
  很显然，多元函数的定义域与一元函数的定义域的表示方式是不一样的：一元函数的定义域是数轴上的一个区间，而多元函数是定义域是点集。比如二元函数 $z = arcsin(x^2+y^2)$ 它的定义域是平面上的一个圆

$$\{(x,y) \;| \;x^2+y^2 \le 1 \}$$
注：为了方便讨论，后面一般只讨论二元函数，多元函数可以另行扩展。
2，二元函数的极限（二重极限）
  函数的极限不同于数列的极限：数列的极限只有 $n \to +\infty$ 一种趋势，而函数的极限可以是 $x \to x_0$ ，即任一点都可以取极限。先回顾一元函数的极限
$$\lim_{x \to x_0} f(x) = A$$
  对于一元函数来讲，自变量被限制在x轴上，根据极限的定义： $x \to x_0$ 的方式只有三种：从左边趋近、从右边趋近、或者在左右两边跳动绝对值趋近。
  二元函数极限的定义是
$$\lim_{(x,y) \to (x_0,y_0)} f(x,y) = A$$
  从上式可以看出，它是平面上的两个点的趋近 $P(x,y) \to P_0(x_0,y_0)$ ，很明显，平面上两个点的趋近方式（路径）有无数种，这就决定了二元极限要比一元极限复杂的多。例：
$$\lim_{(x,y) \to (0,0)} \frac{xy}{x^2+y^2}$$
$(x,y)$ 可以沿不同的直线 $y = kx$ 趋向于原点
$$\lim_{(x,y) \to (0,0)} \frac{xy}{x^2+y^2} = \lim_{x \to 0, y=kx} \frac{xy}{x^2+y^2} = \lim_{x \to 0} \frac{x*kx}{x^2+(kx)^2} = \frac{k}{k^2+1}$$
很明显，极限值是不同的。再来看
$$\lim_{(x,y) \to (0,0)} \frac{x^2+y^2}{x^2+y} = \lim_{x \to 0, y=kx}\frac{x^2+y^2}{x^2+y} = \lim_{x \to 0} \frac{x^2+(kx)^2}{x^2+(kx)} = 0$$
我们能说这个极限存在，且等于0吗？换条路径再看 $y = -x^2 + x^3$
$$\lim_{(x,y) \to (0,0)} \frac{x^2+y^2}{x^2+y} = \lim_{x \to 0, y=-x^2 + x^3}\frac{x^2+y^2}{x^2+y} = \lim_{x \to 0} \frac{x^2+(-x^2 + x^3)^2}{x^3} \to \infty$$
事实上，我们只能以邻域的方式来描述平面上两个点的趋近。
3，求二元函数的极限
  一般利用极限的性质转化为一元函数的极限，例如：
$$\lim_{(x,y) \to (0,2)} \frac{sin(xy)}{x} = \lim_{(x,y) \to (0,2)} [\frac{sin(xy)}{xy} \cdot y] \\ = \lim_{xy \to 0} \frac{sin(xy)}{xy} \cdot \lim_{y \to 2}y = 1 \cdot 2 = 2$$
4,二次极限
  直接看例子，注意它与二重极限的关系
$$\lim_{y \to 0}[\lim_{x \to 0} \frac{xy}{x^2+y^2}] = ?$$
  在求 x 的极限时，将 y 当常数看待，故有
$$\lim_{y \to 0}[\lim_{x \to 0} \frac{xy}{x^2+y^2}] = \lim_{y \to 0}[\lim_{x \to 0} \frac{0 \cdot y}{0^2+y^2}] = \lim_{y \to 0}[0] = 0$$
5，二元函数的连续性
  二元函数的连续性与一元函数的连续性是相似，包括：点连续、一致连续、介值定理、有界性与最大最小值定理。具体可以参考教材。
$$\lim_{(x,y) \to (x_0,y_0)} f(x,y) = f(x_0, y_0)$$
注：关于多元函数的极限和连续性，可以参考 wiki - multivariable calculus

四、课后习题

Exercise 10-1-1-2
  以下 $R^2$ 的子集不是闭区域的是

$$\{(x,y) \; | \; x + y^2 \ge 1 \}$$
解：先画图

import numpy as np
import matplotlib.pyplot as plt
y = np.linspace(-5, 5)
x = 1 - y ** 2
plt.plot(x, y)
plt.grid()
plt.show()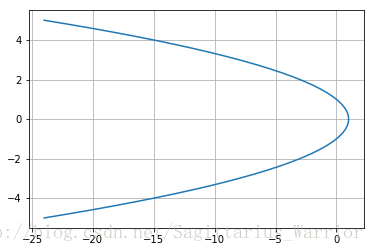

  如上图所示，这个点集位于曲线外围 $y \ge \sqrt{1-x} \; or \; y \le -\sqrt{1-x}$


Exercise 10-1-1-4
  (0,0)是以下函数f(x,y)的定义域的内点的是：

$$f(x,y) = \sqrt{x} ln(x+y)$$
$$f(x,y) = \frac{x+y}{x^2+y^2}$$
$$f(x,y) = arcsin \frac{x}{y}$$
$$f(x,y) = ln(1-x^2-y^2)$$
解： (0,0)是 A 的边界点， B 的聚点，非内点； C 的聚点，边界点， D 的内点。

#Exercise 10-1-1-5
from sympy import *
init_printing()
x,y,u,v = symbols('x y u v')
expr = (3 * u ** 2 * v + v ** 3 ) / 4
simplify(expr.subs({u:(x+y), v:(x-y)}))

$$x^{3} - y^{3}$$