微积分：2.3多元微积分

本课程来自 深度之眼，部分截图来自课程视频。
【第二章 微积分】2.3多元微积分
在线LaTeX公式编辑器

任务详解：

这节课主要介绍了偏导数，多元复合函数求导法则，方向导数与梯度，多元函数泰勒公式，多元函数的极值，矩阵的求导等知识点。
掌握目标：
1、了解偏导数的概念，掌握求法
2、掌握复合偏导数的求法
3、掌握方向导数和梯度
4、了解多元函数的泰勒展开，海森矩阵，极值的充要条件
5、掌握常用矩阵的求导

1.偏导数

定义设函数 $z=f(x,y)$在点 $(x_0,y_0)$的某一邻域内有定义，当 $y$固定在 $y_0$
而 $x$在 $x_0$处有增量 $\Delta x$时，相应的函数有增量
$f(x_0+\Delta x,y_0)-f(x_0,y_0)$
如果：
$\lim_{\Delta x\to 0}\frac{f(x_0+\Delta x,y_0)-f(x_0,y_0)}{\Delta x}\tag{1}$
存在，那么称此极限为函数 $z=f(x,y)$在点 $(x_0,y_0)$处对x的偏导数，记作：
$\frac{\partial z}{\partial x}\bigg|_{\begin{matrix}x=x_0\\ y=y_0\end{matrix}},\frac{\partial f}{\partial x}\bigg|_{\begin{matrix}x=x_0\\ y=y_0\end{matrix}},z_x\bigg|_{\begin{matrix}x=x_0\\ y=y_0\end{matrix}}或f_x(x_0,y_0)$
类似地，函数 $z=f(x,y)$在点 $(x_0,y_0)$处对y的偏导数定义为：
$\lim_{\Delta y\to 0}\frac{f(x_0+\Delta y,y_0)-f(x_0,y_0)}{\Delta y}\tag{2}$
记作：
$\frac{\partial z}{\partial y}\bigg|_{\begin{matrix}x=x_0\\ y=y_0\end{matrix}},\frac{\partial f}{\partial y}\bigg|_{\begin{matrix}x=x_0\\ y=y_0\end{matrix}},z_y\bigg|_{\begin{matrix}x=x_0\\ y=y_0\end{matrix}}或f_y(x_0,y_0)$
偏导数的概念还可推广到二元以上的函数.例如三元函数 $u=f(x,y,z)$在点
$(x,y,z)$处对x的偏导数定义为：
$f_x(x,y,z)=\lim_{\Delta x\to 0}\frac{f(x+\Delta x,y,z)-f(x,y,z)}{\Delta x}$
同理有：
$f_y(x,y,z)=\lim_{\Delta y\to 0}\frac{f(x,y+\Delta y,z)-f(x,y,z)}{\Delta y}$
$f_z(x,y,z)=\lim_{\Delta z\to 0}\frac{f(x,y,z+\Delta z)-f(x,y,z)}{\Delta z}$

---------------------------------------------------------割你没商量1------------------------------------------------------
例子：求 $z=x^2+3xy+y^2$在点(1,2)处的偏导数。
$\frac{\partial z}{\partial x}=2x+3y$
$\frac{\partial z}{\partial y}=3x+2y$
$\frac{\partial z}{\partial x}\bigg |_{(1,2)}=5$
$\frac{\partial z}{\partial y}\bigg |_{(1,2)}=5$
---------------------------------------------------------割你没商量1------------------------------------------------------

二阶偏导数

设函数 $z=f(x,y)$在区域D内具有偏导数
$\frac{\partial z}{\partial x}=f_x(x,y),\frac{\partial z}{\partial y}=f_y(x,y)$
于是在D内 $f_x(x,y)$， $f_y(x,y)$都是x，y的函数.如果这两个函数的偏导数也存在，那么称它们是函数 $z=f(x,y)$的二阶偏导数。按照对变量求导次序的不同有下列四个二阶偏导数：
$\frac{\partial }{\partial x}\left(\frac{\partial z}{\partial x}\right)=\frac{\partial^2z }{\partial x^2}=f_{xx}(x,y),\frac{\partial }{\partial y}\left(\frac{\partial z}{\partial x}\right)=\frac{\partial^2z }{\partial x\partial y}=f_{xy}(x,y)$
$\frac{\partial }{\partial x}\left(\frac{\partial z}{\partial y}\right)=\frac{\partial^2z }{\partial y\partial x}=f_{yx}(x,y),\frac{\partial }{\partial y}\left(\frac{\partial z}{\partial y}\right)=\frac{\partial^2z }{\partial y^2}=f_{yy}(x,y)$

2.多元复合函数求导法则

2.1.一元函数与多元函数复合的情形

定理1如果函数 $u=\varphi(t)$及 $v=\psi(t)$都在点 $t$可导，函数 $z=f(u,v)$在对应点 $(u,v)$具有连续偏导数，那么复合函数： $z=f[\varphi(t),\psi(t)]$在点 $t$可导，且有
$\frac{dz}{dt}=\frac{\partial z}{\partial u}\frac{\partial u}{\partial t}+\frac{\partial z}{\partial v}\frac{\partial v}{\partial t}$

2.2.多元函数与多元函数复合的情形

定理2如果函数 $u=\varphi(x,y)$及 $v=\psi(x,y)$都在点 $(x,y)$具有对x及对y的偏导数，函数 $z=f(u,v)$在对应点 $(u,v)$具有连续偏导数，那么复合函数 $z=f[\varphi(x,y),\psi(x,y)]$在点 $(x,y)$的两个偏导数都存在，且有
$\frac{\partial z}{\partial x}=\frac{\partial z}{\partial u}\frac{\partial u}{\partial x}+\frac{\partial z}{\partial v}\frac{\partial v}{\partial x}$
$\frac{\partial z}{\partial y}=\frac{\partial z}{\partial u}\frac{\partial u}{\partial y}+\frac{\partial z}{\partial v}\frac{\partial v}{\partial y}$

3.方向导数与梯度(重要)

方向导数

以二元函数为例：
$\left\{\begin{matrix}x=x_0+tcos\alpha\\y=y_0+tcos\beta \end{matrix}\right.(t\geq 0)$
t从图像上看实际上就是从 $P_0$到 $P$的距离

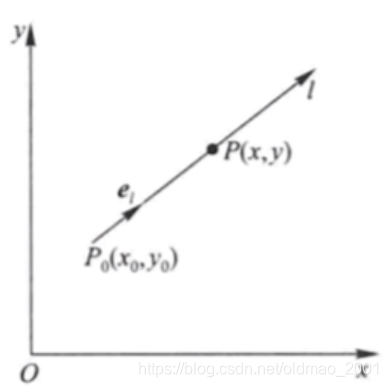
引入方向导数（想要求沿着哪个方向走，x和y的变化最大/快）：
$\frac{\partial f}{\partial l}\bigg|_{x_0,y_0}=\lim_{t\to0^+}\frac{f(x_0+tcos\alpha,y_0+tcos\beta)-f(x_0,y_0)}{t}\tag{3}$

定理如果函数 $f(x,y)$在点 $P_0(x_0,y_0)$可微分，那么函数在该点沿任一方向 $l$的方向导数存在，且有
$\frac{\partial f}{\partial l}\bigg|_{x_0,y_0}=f_x(x_0,y_0)cos\alpha+f_y(x_0,y_0)cos\beta\tag{4}$
等式（4）可以由（3）推出来，证明如下：
---------------------------------------------------------割你没商量2------------------------------------------------------
$(3)=\lim_{t\to0^+}[\frac{f(x_0+tcos\alpha,y_0+tcos\beta)-f(x_0,y_0+tcos\beta)}{t}+\frac{f(x_0,y_0+tcos\beta)-f(x_0,y_0)}{t}]$
分别看加号两边的两项，先看左边，分子分母同时乘上 $cos\alpha$：
$\lim_{t\to0^+}\frac{f(x_0+tcos\alpha,y_0+tcos\beta)-f(x_0,y_0+tcos\beta)}{tcos\alpha}cos\alpha\tag{5}$
当 $t\to0^+$的时候 $tcos\alpha\to0$，所以可以把 $tcos\alpha$看做是 $\Delta x$，式（5）变成：
$\lim_{t\to0^+}\frac{f(x_0+\Delta x,y_0+tcos\beta)-f(x_0,y_0+tcos\beta)}{\Delta x}cos\alpha\tag{6}$
根据最上面偏导数的定义公式（1），把 $y_0+tcos\beta$看成一个整体，可知（6）就是
$f_x(x_0,y_0+tcos\beta)cos\alpha$
由于 $t\to0$，
$f_x(x_0,y_0+tcos\beta)cos\alpha=f_x(x_0,y_0)cos\alpha$
再看右边，，分子分母同时乘上 $cos\beta$：
$\lim_{t\to0^+}\frac{f(x_0,y_0+tcos\beta)-f(x_0,y_0)}{tcos\beta}cos\beta\tag{7}$
同样的，把 $tcos\beta$看做是 $\Delta y$，式（7）变成：
$\lim_{t\to0^+}\frac{f(x_0,y_0+\Delta y)-f(x_0,y_0)}{\Delta y}cos\beta\tag{8}$
根据最上面偏导数的定义公式（2），可知（8）就是：
$f_y(x_0,y_0)cos\beta$
所以（4）=（3），搞定。
---------------------------------------------------------割你没商量2------------------------------------------------------

梯度

与方向导数有关联的一个概念是函数的梯度。在二元函数的情形，设函数 $f(x,y)$在平面区域D内具有一阶连续偏导数，则对于每一点 $P_0(x_0,y_0)\in D$，都可定出一个向量
$f_x(x_0,y_0)i+f_y(x_0,y_0)j$
这向量称为函数 $f(x,y)$在点 $P_0(x_0,y_0)$的梯度，记作grad $f(x_0,y_0)$或 $\triangledown f(x_0,y_0)$，即
$grad\space f(x_0,y_0)=\triangledown f(x_0,y_0)=f_x(x_0,y_0)i+f_y(x_0,y_0)j$
如果函数 $f(x,y)$在点 $P_0(x_0,y_0)$可微分， $e_l=(cos\alpha,cos\beta)$是与方向 $l$同向的单位向量，那么
$\frac{\partial f}{\partial l}\bigg|_{x_0,y_0}=f_x(x_0,y_0)cos\alpha+f_y(x_0,y_0)cos\beta\tag{4}$
两个向量的点积可以写成两个向量的模长乘以夹角的余弦值。 $\theta=0$的时候变量变化得最快。
$=grad\space f(x_0,y_0)\cdot e_l=|grad\space f(x_0,y_0)|cos\theta$

4.多元函数泰勒公式

多元函数泰勒公式

以上是比较晦涩的公式，实际使用中，只要展开的前面两项
$f(x_0+\Delta x,y_0+\Delta y)=f(x_0,y_0)+\tag{9}$
$f_x(x_0,y_0)\Delta x+f_y(x_0,y_0)\Delta y+\tag{10}$
$f_{xx}(x_0,y_0)\Delta x^2+2f_{xy}(x_0,y_0)\Delta x\Delta y+f_{yy}(x_0,y_0)\Delta y^2\tag{11}$
可以看到（9）是0次项，（10）是一次项，（11）是二次项，后面的三次项一般都省略不用。
（10）可以看做是：
$\begin{bmatrix}f_x& f_y\end{bmatrix}\begin{bmatrix}\Delta x\\ \Delta y\end{bmatrix}=\triangledown f^T\begin{bmatrix}\Delta x\\ \Delta y\end{bmatrix}$
（11）可以看做是：
$\begin{bmatrix}\Delta x& \Delta y\end{bmatrix}\begin{bmatrix}f_{xx}&f_{xy}\\f_{xy}&f_{yy}\end{bmatrix}\begin{bmatrix}\Delta x\\ \Delta y\end{bmatrix}$
$\begin{bmatrix}f_{xx}&f_{xy}\\f_{xy}&f_{yy}\end{bmatrix}$称为hessian矩阵。

海森矩阵（二维或高维）

把上面的二元推广到多元，例如，设函数为 $f(x_1,x_2,...,x_n)$，则它的泰勒展开为：
$f(x_1+\Delta x_1,x_2+\Delta x_2,...,x_n+\Delta x_n)=f(x_1,x_2,...,x_n)+$
$\begin{bmatrix}\Delta x_1&\Delta x_2&\cdots&\Delta x_n\end{bmatrix}\begin{bmatrix}f_{x_1}(x_1,x_2,...,x_n)\\ f_{x_2}(x_1,x_2,...,x_n)\\\vdots\\f_{x_n}(x_1,x_2,...,x_n)\end{bmatrix}+$
$\begin{bmatrix}\Delta x_1&\Delta x_2&\cdots&\Delta x_n\end{bmatrix}[Hessian \space Matrix\space H]_{n×n}\begin{bmatrix}\Delta x_1\\\Delta x_2\\\vdots\\\Delta x_n\end{bmatrix}$
中间的黑神矩阵的通项为： $h_{ij}=\frac{\partial^2f}{\Delta x_i\Delta x_j}$
例如矩阵第一行为： $f_{x_1x_1},f_{x_1x_2},...,_{x_1x_n}$
黑神矩阵是对称矩阵。

5.多元函数的极值

定义设函数 $z=f(x,y)$的定义域为 $D$， $P_0(x_0,y_0)$为D的内点。若存在 $P_0$
的某个邻域 $U(P_0)\subset D$，使得对于该邻域内异于 $P_0$的任何点 $(x,y)$，都有
$f(x,y)<f(x_0,y_0)$
则称函数 $f(x,y)$在点 $(x_0,y_0)$有极大值 $f(x_0,y_0)$，点 $(x_0,y_0)$称为函数 $f(x,y)$的极大值点；
若对于该邻域内异于 $P_0$的任何点 $(x,y)$，都有
$f(x,y)>f(x_0,y_0)$
则称函数 $f(x,y)$在点 $(x_0,y_0)$有极小值 $f(x_0,y_0)$，点 $(x_0,y_0)$称为函数 $f(x,y)$的极小值点.
极大值与极小值统称为极值.使得函数取得极值的点称为极值点.

定理1（必要条件）设函数 $z=f(x,y)$在点 $(x_0,y_0)$具有偏导数，且在点 $(x_0,y_0)$处有极值，则有
$f_x(x_0,y_0)=0,f_y(x_0,y_0)=0$
定理2（充分条件）设函数 $z=f(x,y)$在点 $(x_0,y_0)$的某邻域内连续且有一阶及二阶连续偏导数，又 $f_x(x_0,y_0)=0,f_y(x_0,y_0)=0$，令
$f_{xx}(x_0,y_0)=A，f_{xy}(x_0,y_0)=B，f_{yy}(x_0,y_0)=C$
则 $f(x,y)$在 $(x_0,y_0)$处是否取得极值的条件如下：
（1） $AC-B^2>0$时具有极值，且当 $A<0$时有极大值，当 $A>0$时有极小值；
（2） $AC-B^2<0$时没有极值；
（3） $AC-B^2=0$时可能有极值，也可能没有极值，还需另作讨论.
这里可以看到 $\begin{bmatrix}f_{xx}&f_{xy}\\f_{xy}&f_{yx}\end{bmatrix}=\begin{bmatrix}A&B\\B&C\end{bmatrix}$是黑神矩阵。
---------------------------------------------------------割你没商量3------------------------------------------------------
这里吧充分条件进行证明。
假设 $(x,y)$是领域内的一个点，则在这个点上用泰勒展开得：
$f(x,y)=f(x_0,y_0)+\triangledown f^T(x,y)\begin{bmatrix}x-x_0\\ y-y_0\end{bmatrix}+\frac{1}{2}\begin{bmatrix}x-x_0& y-y_0\end{bmatrix}\begin{bmatrix}A&B\\B&C\end{bmatrix}\begin{bmatrix}x-x_0\\ y-y_0\end{bmatrix}\tag{12}$
由于 $f_x(x_0,y_0)=0,f_y(x_0,y_0)=0$，所以 $\triangledown f^T(x,y)\begin{bmatrix}x-x_0\\ y-y_0\end{bmatrix}=0$
令 $x-x_0=\Delta x,y-y_0=\Delta y$，式（12）变成：
$=f(x_0,y_0)+\frac{1}{2}\begin{bmatrix}\Delta x& \Delta y\end{bmatrix}\begin{bmatrix}A&B\\B&C\end{bmatrix}\begin{bmatrix}\Delta x\\ \Delta y\end{bmatrix}\tag{13}$
---------------------------------------------------------割你没商量3.1----------------------------------------------------
之前讨论正定矩阵的时候有过结论：
一个矩阵M是正定矩阵，则在他的左右两边乘以向量及向量转置大于等于0： $u^tMu\geq0$
一个矩阵M不是正定矩阵，则在他的左右两边乘以向量及向量转置大于等于0： $u^tMu<0$
---------------------------------------------------------割你没商量3.1----------------------------------------------------
从式（13）可知，如果 $\begin{bmatrix}A&B\\B&C\end{bmatrix}$正定， $f(x,y)=f(x_0,y_0)+正数$，即 $f(x,y)>f(x_0,y_0)$， $(x_0,y_0)$是极小值；
如果 $\begin{bmatrix}A&B\\B&C\end{bmatrix}$负定， $f(x,y)=f(x_0,y_0)+负数$，即 $f(x,y)<f(x_0,y_0)$， $(x_0,y_0)$是极大值；
---------------------------------------------------------割你没商量3.2----------------------------------------------------
接下来要判断矩阵啥时候正定，根据正定的定理可知，如果一个矩阵正定，那么它的所有特征值要大于0。如果一个矩阵不正定，那么它的所有特征值要小于0。
---------------------------------------------------------割你没商量3.2----------------------------------------------------
上面 $\begin{bmatrix}A&B\\B&C\end{bmatrix}$的特征值行列式为：
$\begin{vmatrix}A-\lambda&B\\B&C-\lambda\end{vmatrix}=(\lambda-A)(\lambda-C)-B^2$
$=\lambda^2-(A+C)\lambda+AC-B^2=0$
情况1：正定，即 $\lambda_1>0,\lambda_2>0\to A+C>0 and AC-B^2>0$（韦达定理）
情况2：负定，即 $\lambda_1<0,\lambda_2<0\to A+C<0 and AC-B^2>0$（韦达定理）
无论是正定还是负定，都会有极值，也就是都满足条件 $AC-B^2>0$，也就是 $AC>B^2$，意味AC同号，
情况一的时候A+C>0 ，此时AC都要为正数，即A>0时， $\begin{bmatrix}A&B\\B&C\end{bmatrix}$正定且有极小值；
情况二的时候A+C<0 ，此时AC都要为负数，即A<0时， $\begin{bmatrix}A&B\\B&C\end{bmatrix}$负定且有极大值。
条件（1）得证。其他两个条件证明省略。
---------------------------------------------------------割你没商量3------------------------------------------------------

6.矩阵的求导

常见性质
1. $f(x)=Ax$，则
$\frac{\partial f(x)}{\partial x^T}=\frac{\partial Ax}{\partial x^T}=A$
2. $f(x)=x^TAx$，则
$\frac{\partial f(x)}{\partial x}=\frac{\partial (x^TAx)}{\partial x^T}=Ax+A^Tx$
3. $f(x)=a^Tx$，则
$\frac{\partial a^Tx}{\partial x}=\frac{\partial x^Ta}{\partial x}=a$
4. $f(x)=x^TAy$.则
$\frac{\partial xa^TAy}{\partial x}=Ay$
$\frac{\partial xa^TAy}{\partial A}=xy^T$
要搞清楚矩阵求导之后变成一个矩阵还是一个值？

矩阵求导公式大全