原根求解方法

关于指数和原根的基础知识参见博文《指数和原根》. 本文的部分内容也是对该博文的补充.

记号

(1) X ( d ) : = { n ∈ Z :   1 ≤ n < p ,   n 对 模 p 的 指 数 = d } X\left( d \right):=\left\{ n\in \mathbb{Z}:\text{ }1\le n<p,\text{ }n对模p的指数=d \right\} X(d):={ n∈Z: 1≤n<p, n对模p的指数=d}, 其中$p$是一个素数, $d$满足$d|p-1$.
(2) $p^i\Vert x\iff p^i|x\wedge p^{i+1}\cancel{|}x.$

引理1: 设$d$是$x_0$对模$m$的指数, 则$\forall x\in \mathbb{Z}$满足$x\equiv x_0\mathrm{m}\mathrm{o}\mathrm{d}m$, $x$对模$m$的指数也为$d$. 此时称集合 { x ∈ Z : x ≡ x 0     m o d   m } \left\{ x\in \mathbb{Z}:x\equiv { {x}_{0}}\text{ }\bmod m \right\} { x∈Z:x≡x0​ modm}为模$m$的一个指数. 特别地, 若$d=\phi \left(m\right)$, 则称集合 { x ∈ Z : x ≡ x 0     m o d   m } \left\{ x\in \mathbb{Z}:x\equiv { {x}_{0}}\text{ }\bmod m \right\} { x∈Z:x≡x0​ modm}为模$m$的一个原根.

证明 记 S 0 = { n ∈ Z > 0 : x 0 n ≡ 1     m o d   m } { {S}_{0}}=\left\{ n\in { {\mathbb{Z}}_{>0}}:{ {x}_{0}}^{n}\equiv 1\text{ }\bmod m \right\} S0​={ n∈Z>0​:x0​n≡1 modm}.
$\forall x\in \mathbb{Z}$满足$x\equiv x_0\mathrm{m}\mathrm{o}\mathrm{d}m$, 记 S x = { n ∈ Z > 0 : x n ≡ 1     m o d   m } { {S}_{x}}=\left\{ n\in { {\mathbb{Z}}_{>0}}:{ {x}^{n}}\equiv 1\text{ }\bmod m \right\} Sx​={ n∈Z>0​:xn≡1 modm}.
由$x$与$x_0$对模$m$的同余关系, 显然有$S_0=S_x$, 则$\min S_x=\min S_0=d$, 即$d$也是$x$对模$m$的指数.

引理2: 若$p$是奇素数, 则模$p$的原根是存在的.

证明 由于$p$是奇素数, 因此 ∀ x ∈ { 1 , 2 , ⋯   , p − 1 } \forall x\in \left\{ 1,2,\cdots ,p-1 \right\} ∀x∈{ 1,2,⋯,p−1}, $\gcd \left(x,p\right)=1$. 根据博文《指数和原根》命题2, $x$对模$p$的指数存在. 基于此, 从这$p-1$个指数中取出所有不同的指数, 记作
$${\delta }_1,{\delta }_2,\cdots ,{\delta }_r.\text{\hspace{1em}(2.1)}$$
令$\tau =lcm\left({\delta }_1,{\delta }_2,\cdots ,{\delta }_r\right)$.

第一步, 我们证明$\exists g\in \mathbb{Z}$, $g$对模$p$的指数是$\tau$.
设$\tau ={q_1}^{{\alpha }_1}{q_2}^{{\alpha }_2}\cdots {q_k}^{{\alpha }_k}$是$\tau$的标准分解式. ∀ s ∈ { 1 , 2 , ⋯   , k } \forall s\in \left\{ 1,2,\cdots ,k \right\} ∀s∈{ 1,2,⋯,k}, 设${q_s}^{{\beta }_{s1}}\Vert {\delta }_1,{q_s}^{{\beta }_{s2}}\Vert {\delta }_2,\cdots ,{q_s}^{{\beta }_{sr}}\Vert {\delta }_r$. 则成立
α s = max ⁡ { β s 1 , β s 2 , ⋯   , β s r } , { {\alpha }_{s}}=\max \left\{ { {\beta }_{s1}},{ {\beta }_{s2}},\cdots ,{ {\beta }_{sr}} \right\}, αs​=max{ βs1​,βs2​,⋯,βsr​},
即 ∃ δ ∈ { δ 1 , δ 2 , ⋯   , δ r } \exists \delta \in \left\{ { {\delta }_{1}},{ {\delta }_{2}},\cdots ,{ {\delta }_{r}} \right\} ∃δ∈{ δ1​,δ2​,⋯,δr​}, 使得${q_s}^{{\alpha }_s}\Vert \delta$, 即$\exists t\in \mathbb{Z}$, 使得$\delta =t{q_s}^{{\alpha }_s}$. 根据式(2.1)的定义, ∃ x ∈ { 1 , 2 , ⋯   , p − 1 } \exists x\in \left\{ 1,2,\cdots ,p-1 \right\} ∃x∈{ 1,2,⋯,p−1}, 使得$x$对模$p$的指数为$\delta$. 根据博文《指数和原根》定理7, $x_s=x^t$对模$p$的指数为${q_s}^{{\alpha }_s}$. 依照上面方法分别找出模$p$指数为${q_1}^{{\alpha }_1},{q_2}^{{\alpha }_2},\cdots ,{q_k}^{{\alpha }_k}$的整数$x_1,x_2,\cdots ,x_k$. 由于$\gcd \left({q_1}^{{\alpha }_1},{q_2}^{{\alpha }_2},\cdots ,{q_k}^{{\alpha }_k}\right)=1$, 根据博文《指数和原根》定理8, $g:=x_1{x}_2\cdots x_k$对模$p$的指数即为$\prod _{s=1}^k{q_s}^{{\alpha }_s}=\tau$.

第二步, 我们证明$\tau =p-1$.
一方面, $1,2,\cdots ,p-1$中任一数的指数都在式(2.1)中出现, 而 ∀ s ∈ { 1 , 2 , ⋯   , r } \forall s\in \left\{ 1,2,\cdots ,r \right\} ∀s∈{ 1,2,⋯,r}, ${\delta }_s|\tau$, 故成立
x τ ≡ 1     m o d   p ,   ∀ x ∈ { 1 , 2 , ⋯   , p − 1 } , { {x}^{\tau }}\equiv 1\text{ }\bmod p,\text{ }\forall x\in \left\{ 1,2,\cdots ,p-1 \right\}, xτ≡1 modp, ∀x∈{ 1,2,⋯,p−1},
即同余式$x^{\tau }\equiv 1\mathrm{m}\mathrm{o}\mathrm{d}p$至少有$p-1$个解. 由博文《素数模同余式次数与其解数的关系》定理5, $\tau \ge p-1$.
另一方面, 由于$p$是奇素数, ∀ x ∈ { 1 , 2 , ⋯   , p − 1 } \forall x\in \left\{ 1,2,\cdots ,p-1 \right\} ∀x∈{ 1,2,⋯,p−1}, $\gcd \left(x,p\right)=1$. 由欧拉定理, 成立$x^{\phi \left(p\right)}=x^{p-1}\equiv 1\mathrm{m}\mathrm{o}\mathrm{d}p$. 再由博文《指数和原根》定理5, 有 ∀ s ∈ { 1 , 2 , ⋯   , r } \forall s\in \left\{ 1,2,\cdots ,r \right\} ∀s∈{ 1,2,⋯,r}, ${\delta }_s|p-1$. 再由最小公倍数的性质, 有$\tau =lcm\left({\delta }_1,{\delta }_2,\cdots ,{\delta }_r\right)|p-1$, 由此得$\tau \le p-1$.
综上有$\tau =p-1$.

基于前两步, $\exists g\in \mathbb{Z}$使得$g$对模$p$的指数为$p-1=\phi \left(p\right)$, $g$即为模$p$的一个原根. 至此引理2证明完毕.

引理3: 设$p$是素数, 若$d|p-1$, 则一定有$X\left(d\right)\ne \varnothing$.

证明 $d|p-1\Rightarrow \exists k\in \mathbb{Z}$使得$p-1=kd$。由引理2, $\exists g\in \mathbb{Z}$使得$g$是模$p$的原根, 即$g$对模$p$的指数为$\phi \left(p\right)=p-1=kd$. 由博文《指数和原根》定理7, $g^k$对模$p$的指数即为$d$, 即有$\left(g^k\mathrm{m}\mathrm{o}\mathrm{d}p\right)\in X\left(d\right)$, $X\left(d\right)\ne \varnothing$.

引理4: 设$p$为素数, 若$d|p-1$, 则有$\left|X\left(d\right)\right|=\phi \left(d\right)$.

证明
第一步, 由引理3, $X\left(d\right)\ne \varnothing$, $\exists a\in X\left(d\right)$. 则$a$对模$p$的指数为$d$, 有
$$a^d\equiv 1\mathrm{m}\mathrm{o}\mathrm{d}p.\text{\hspace{1em}(4.1)}$$
记
$$S=\left\{1\le x<p:x^d\equiv 1\mathrm{m}\mathrm{o}\mathrm{d}p\right\}.$$
显然有$X\left(d\right)\subseteq S$. 由于$d|p-1$, 因此$\exists k\in \mathbb{Z}$, 使得$p-1=kd$. 成立
$$\begin{array}{rl}& x^p-x=x\left(x^{p-1}-1\right)=x\left(x^{kd}-1\right)\\ & =x\left({\left(x^d\right)}^k-1\right)=x\left(x^d-1\right)\left({\left(x^d\right)}^{k-1}+{\left(x^d\right)}^{k-2}+\cdots +{\left(x^d\right)}^1+1\right).\end{array}$$
即有$x^d-1|x^p-x$, $x^d-1$除$x^p-x$得到的余式是$0$, 由博文《素数模同余式次数与其解数的关系》定理6, 同余式$x^d\equiv 1\mathrm{m}\mathrm{o}\mathrm{d}p$恰好有$d$个根.
另一方面, 由式(4.1), 成立${\left(a^k\right)}^d={\left(a^d\right)}^k\equiv 1\mathrm{m}\mathrm{o}\mathrm{d}p$, 因此$1,a,a^2,\cdots ,a^{d-1}$这$d$个数均为同余式$x^d\equiv 1\mathrm{m}\mathrm{o}\mathrm{d}p$的根. 且根据博文《指数和原根》定理5(1), $1,a,a^2,\cdots ,a^{d-1}$两两不同余, 因此$S$可表示为
$$S=\left\{x\mathrm{m}\mathrm{o}\mathrm{d}p,x\in \left\{1,a,a^2,\cdots ,a^{d-1}\right\}\right\}\supseteq X\left(d\right).\text{\hspace{1em}(4.2)}$$

第二步, 由博文《指数和原根》定理9, $a^k$对模$p$的指数为$\frac{d}{\gcd \left(d,k\right)}$. 因此成立推理
$$\left(a^k\mathrm{m}\mathrm{o}\mathrm{d}p\right)\in X\left(d\right)\Rightarrow \frac{d}{\gcd \left(d,k\right)}=d\Rightarrow \gcd \left(d,k\right)=1.$$
由式(4.2), $X\left(d\right)$中的元素均为$\left(a^k\mathrm{m}\mathrm{o}\mathrm{d}p\right)$的形式, 因此有$$\left|X\left(d\right)\right|\le \phi \left(d\right).\text{\hspace{1em}(4.3)}$$

第三步, 一方面, ∀ n ∈ { 1 , 2 , ⋯   , p − 1 } \forall n\in \left\{ 1,2,\cdots ,p-1 \right\} ∀n∈{ 1,2,⋯,p−1}, 由于$p$是素数, $\gcd \left(n,p\right)=1$, 因此$n$对模$p$的指数存在, 设为$d_n$, 成立$n\in X\left(d_n\right)$. 由费马小定理, 成立$n^{p-1}\equiv 1\mathrm{m}\mathrm{o}\mathrm{d}p$. 根据博文《指数和原根》定理5(3), 有$d_n|p-1$.于是成立
{ n ∈ Z :   1 ≤ n < p } ⊆ ⋃ d ∣ p − 1 X ( d ) . (4.4) \left\{ n\in \mathbb{Z}:\text{ }1\le n<p \right\}\subseteq \bigcup\limits_{\left. d \right|p-1}^{ {}}{X\left( d \right)}. \tag{4.4} { n∈Z: 1≤n<p}⊆d∣p−1⋃​X(d).(4.4)
另一方面, 由$X\left(d\right)$的定义, 有$\forall d$满足$d|p-1$, X ( d ) ⊆ { n ∈ Z :   1 ≤ n < p } X\left( d \right)\subseteq \left\{ n\in \mathbb{Z}:\text{ }1\le n<p \right\} X(d)⊆{ n∈Z: 1≤n<p}, 即成立
⋃ d ∣ p − 1 X ( d ) ⊆ { n ∈ Z :   1 ≤ n < p } . (4.5) \bigcup\limits_{\left. d \right|p-1}^{ {}}{X\left( d \right)}\subseteq \left\{ n\in \mathbb{Z}:\text{ }1\le n<p \right\}. \tag{4.5} d∣p−1⋃​X(d)⊆{ n∈Z: 1≤n<p}.(4.5)
由式(4.4), 式(4.5), 成立
⋃ d ∣ p − 1 X ( d ) = { n ∈ Z :   1 ≤ n < p } . (4.6) \bigcup\limits_{\left. d \right|p-1}^{ {}}{X\left( d \right)}=\left\{ n\in \mathbb{Z}:\text{ }1\le n<p \right\}. \tag{4.6} d∣p−1⋃​X(d)={ n∈Z: 1≤n<p}.(4.6)

第四步, 由博文《初等数论 课堂笔记 第三章 – 欧拉函数》中的定理, 成立
$$\sum _{d|p-1}\phi \left(d\right)=p-1.\text{\hspace{1em}(4.7)}$$
由式(4.6), (4.3), (4.7), 成立
$$\begin{array}{rl}& p-1=\left|\bigcup _{d|p-1}X\left(d\right)\right|=\sum _{d|p-1}\left|X\left(d\right)\right|\left(不同的X\left(d\right)彼此互不相交\right)\\ & \le \sum _{d|p-1}\phi \left(d\right)=p-1.\end{array}$$
因此只能是$\forall d$满足$d|p-1$, 成立
$$\left|X\left(d\right)\right|=\phi \left(d\right).$$

推论5: 设$p$是素数, $d|p-1$, 则有$$X\left(d\right)=\left\{\left(a^k\mathrm{m}\mathrm{o}\mathrm{d}p\right):\gcd \left(d,k\right)=1\right\}.$$

证明 首先, 由式(4.2), $\forall x\in X\left(d\right)$, ∃ k ∈ { 0 , 1 , ⋯   , d − 1 } \exists k\in \left\{ 0,1,\cdots ,d-1 \right\} ∃k∈{ 0,1,⋯,d−1}, 使得
$$x=\left(a^k\mathrm{m}\mathrm{o}\mathrm{d}p\right).$$
且在引理4第二步中已经得到推理
$$\left(a^k\mathrm{m}\mathrm{o}\mathrm{d}p\right)\in X\left(d\right)\Rightarrow \frac{d}{\gcd \left(d,k\right)}=d\Rightarrow \gcd \left(d,k\right)=1.$$
若$\exists k$满足$\gcd \left(d,k\right)=1$, 而$a^k\mathrm{m}\mathrm{o}\mathrm{d}p\notin X\left(d\right)$, 则有$\left|X\left(d\right)\right|<\phi \left(d\right)$, 矛盾. 由反证法即可证得推论5.

推论6: 设$p$是素数, 则模$p$的原根有$\phi \left(p-1\right)$个.

证明 根据引理4, 模$p$的原根个数即为$\left|X\left(p-1\right)\right|=\phi \left(p-1\right)>0$.

方法7: 设$p$是素数, 用穷举法求一个数 n ∈ { 1 , 2 , ⋯   , p − 1 } n\in \left\{ 1,2,\cdots ,p-1 \right\} n∈{ 1,2,⋯,p−1}对模$p$的指数.

由于 ∀ n ∈ { 1 , 2 , ⋯   , p − 1 } \forall n\in \left\{ 1,2,\cdots ,p-1 \right\} ∀n∈{ 1,2,⋯,p−1}, $\gcd \left(n,p\right)=1$, 由费马小定理, 成立
$$n^{p-1}\equiv 1\mathrm{m}\mathrm{o}\mathrm{d}p.$$
由博文《指数和原根》命题2和定理5(3), $n$对$p$的指数存在, 记为$\delta$, 满足$\delta |p-1$.
于是我们只需要从小到大逐个地用$p-1$的因数$d$考察是否成立$n^d\equiv 1\mathrm{m}\mathrm{o}\mathrm{d}p$即可.

例子8 (用方法7找出一些小素数的所有原根)

模数$p=3$, $p-1=2$的所有因数是$1,2$.
$$\begin{array}{ccc}& 1& 2\\ 1& 1& \\ 2& 2& 4\equiv 1\end{array}\Rightarrow \begin{array}{ccc}1\le n<3& 1& 2\\ n的指数& 1& 2\end{array}$$
模数$p=5$, $p-1=4$的所有因数是$1,2,4$.
$$\begin{array}{cccc}& 1& 2& 4\\ 1& 1& & \\ 2& 2& 4& 16\equiv 1\\ 3& 3& 9\equiv 4& 81\equiv 1\\ 4& 4& 16\equiv 1& \end{array}\Rightarrow \begin{array}{ccccc}1\le n<5& 1& 2& 3& 4\\ n的指数& 1& 4& 4& 2\end{array}$$
模数$p=7$, $p-1=6$的所有因数是$1,2,3,6$.
$$\begin{array}{ccccc}& 1& 2& 3& 6\\ 1& 1& & & \\ 2& 2& 4& 8\equiv 1& \\ 3& 3& 9\equiv 2& 27\equiv -1& 729\equiv 1\\ 4& 4& 16\equiv 2& 64\equiv 1& \\ 5& 5& 25\equiv 4& 125\equiv -1& 15625\equiv 1\\ 6& 6& 36\equiv 1& & \end{array}\Rightarrow \begin{array}{ccccccc}1\le n<7& 1& 2& 3& 4& 5& 6\\ n的指数& 1& 3& 6& 3& 6& 2\end{array}$$
汇总成如下表格.
$$\begin{array}{ccccc}素数p& 2& 3& 5& 7\\ p的原根个数\phi \left(p-1\right)& 1& 1& 2& 2\\ p的原根& 1& 2& 2,3& 3,5\end{array}$$

方法9: 用推论5和穷举法求一个较大素数$p$的所有原根.

令$n=2$.
第一步: 用方法7求出$n$模$p$的指数$d$.
第二步: 若$d=\phi \left(p\right)=p-1$, 则转第三步, 否则令$n=n+1$, 返回第一步.
第三步: 此时$n$是模$p$的最小原根. 找出 { 1 , 2 , ⋯   , p − 1 } \left\{ 1,2,\cdots ,p-1 \right\} { 1,2,⋯,p−1}中所有与$p-1$互素的数$k$.
第四步: 根据推论5的结果, 依次计算$n^k\mathrm{m}\mathrm{o}\mathrm{d}p$.

注 第一, 二步中最小原根的寻找也可以通过查表法.

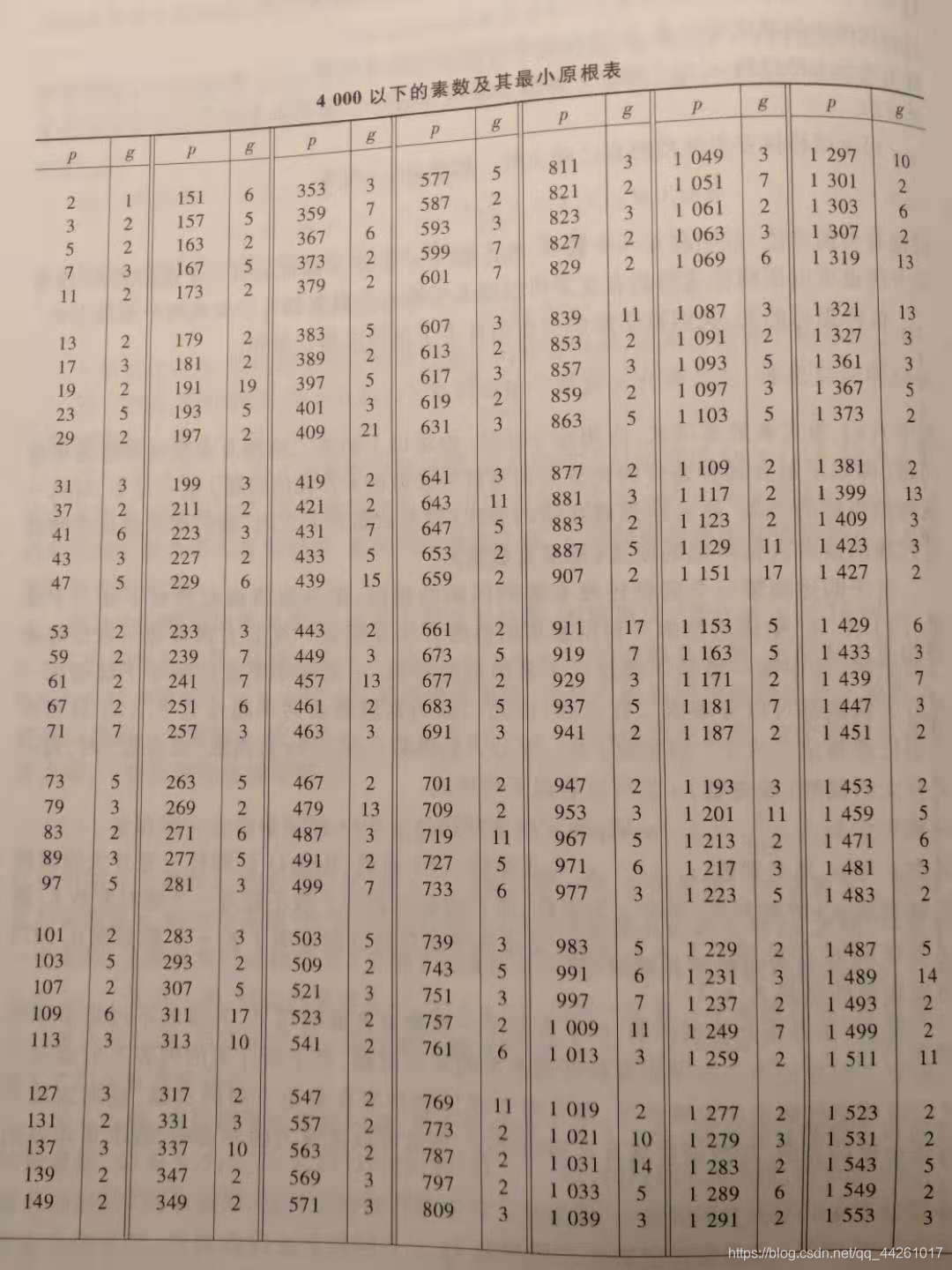
例子10 (用方法9找出一些较大素数的所有原根)

$11$的原根: 因为下面的计算, $g=2$是最小原根, 其他原根上方的$n$与$11-1=10$互素.
$$\begin{array}{ccccccccccc}n& 1& 2& 3& 4& 5& 6& 7& 8& 9& 10\\ 2^n\mathrm{m}\mathrm{o}\mathrm{d}11& \underline{2}& 4& \underline{8}& 5& 10& 9& \underline{7}& 3& \underline{6}& 1\end{array}$$
$13$的原根: 因为下面的计算, $g=2$是最小原根, 其他原根上方的$n$与$13-1=12$互素.
$$\begin{array}{ccccccccccccc}n& 1& 2& 3& 4& 5& 6& 7& 8& 9& 10& 11& 12\\ 2^n\mathrm{m}\mathrm{o}\mathrm{d}13& \underline{2}& 4& 8& 3& \underline{6}& 12& \underline{11}& 9& 5& 10& \underline{7}& 1\end{array}$$
$17$的原根: 因为下面的计算, $g=3$是最小原根, 其他原根上方的$n$与$17-1=16$互素.
$$\begin{array}{ccccccccccccccccc}n& 1& 2& 3& 4& 5& 6& 7& 8& 9& 10& 11& 12& 13& 14& 15& 16\\ 2^n\mathrm{m}\mathrm{o}\mathrm{d}17& 2& 4& 8& 16& 15& 13& 9& 1& & & & & & & & \\ 3^n\mathrm{m}\mathrm{o}\mathrm{d}17& \underline{3}& 9& \underline{10}& 13& \underline{5}& 15& \underline{11}& 16& \underline{14}& 8& \underline{7}& 4& \underline{12}& 2& \underline{6}& 1\end{array}$$
$19$的原根: 因为下面的计算, $g=2$是最小原根, 其他原根上方的$n$与$19-1=18$互素.
$$\begin{array}{ccccccccccccccccccc}n& 1& 2& 3& 4& 5& 6& 7& 8& 9& 10& 11& 12& 13& 14& 15& 16& 17& 18\\ 2^n\mathrm{m}\mathrm{o}\mathrm{d}19& \underline{2}& 4& 8& 16& \underline{13}& 7& \underline{14}& 9& 18& 17& \underline{15}& 11& \underline{3}& 6& 12& 5& \underline{10}& 1\end{array}$$
汇总得到如下结果.
$$\begin{array}{ccccc}素数p& 11& 13& 17& 19\\ p的原根个数\phi \left(p-1\right)& 4& 4& 8& 6\\ p的原根& 2,6,7,8& 2,6,7,11& 3,5,6,7,10,11,12,14& 2,3,10,13,14,15\end{array}$$

例子11 (找出一些合数的所有原根)

(1) $2^2=4$仅有1个原根, 为3.
$$\begin{array}{ccc}n\mathrm{m}\mathrm{o}\mathrm{d}4,\gcd \left(n,4\right)=1& 1& 3\\ n的指数& 1& 2=\phi \left(4\right)\end{array}$$
注 表中只考虑$\gcd \left(n,4\right)=1$的数$n$的理论依据是博文《指数和原根》定理12, 下同.

(2) $6$仅有1个原根, 为$5$.
$$\begin{array}{ccc}n\mathrm{m}\mathrm{o}\mathrm{d}6,\gcd \left(n,6\right)=1& 1& 5\\ n的指数& 1& 2=\phi \left(6\right)\end{array}$$

(3) $8$没有原根, 因为$\phi \left(8\right)=4$且
$$\begin{array}{ccccc}n\mathrm{m}\mathrm{o}\mathrm{d}8,\gcd \left(n,8\right)=1& 1& 3& 5& 7\\ n的指数& 1& 2& 2& 2\end{array}$$