MATLAB 系统仿真与建模（十）—— 频域响应分析

日期：2020.12.30

参考：

1. 控制理论 MATLAB 教程

1 绘制伯德图（bode）

bode 图是直角坐标图

bode 命令可以计算连续线性时不变（定常）系统频域响应的幅值和相角，示例代码如下：

bode(num,den) 
bode(num,den,w) 
bode(A,B,C,D)
bode(A,B,C,D,w)
bode(A,B,C,D,iu,w) 
bode(sys)

不带左端参数的时候屏幕上会直接绘制出伯德图。图中幅值单位为分贝（dB）

当使用左端参数：

[mag, phase, w] = bode(num, den, w); % 其他同理

矩阵mag 和 phase 分别包含系统频率响应在指定频率点上算得的幅值和相角。相角的单位为度 (°) 。 幅值可以通过如下语句转换为分贝值：

magdB = 20*log10(mag);

如果需要指定频率范围，可使用命令：

w = logspace(d1, d2); % 在十倍频程 10^d1 和 10^d2 内生成一个包含50个点的，呈对数均匀分布的向量（包含起点和终点）
w = logspace(d1, d2, n); % 十倍频程 10^d1 和 10^d2 内 生成呈对数均匀分布的n个点(n个频率点包含起点和终点）

eg. 如下传递函数，绘制 bode 图：
$$G(s)=\frac{25}{s^2+4s+25}$$
代码如下：

num = [0 0 25];
den = [1 4 25];
G = tf(num, den);
bode(G)
grid
title('Bode Diagram of G(s)=25/(s^2+4s+25)')

绘制出图片如下：

如果期望幅值的范围介于某一范围之间（例如-50dB~50dB之间），就可以在伯德图上添加幅值为-50dB和50dB两条直线。

如果期望相角的范围在-150°~150°之间，举个例子：

系统如下：
$$G(s)=\frac{9(s^2+0.2s+1)}{s(s^2+1.2s+9)}$$
我们规定范围内绘制bode图，代码如下：

num = [9 1.8 9];
den = [1 1.2 9 0];
w = logspace(-2, 3, 100);
[mag, phase, w] = bode(num, den, w);
magdB = 20*log10(mag);
dBmax = 50*ones(1,100); 
dBmin = -50*ones(1,100); %点数必须与 w 中频率点的数目相等

% ********************************************************************
subplot(2, 1, 1)
semilogx(w, magdB, 'o', w, magdB, '-', w, dBmax, '--', w, dBmin, ':')、
grid
title('BodeDiagram of G(s)=9(s^2+0.2s+1)/(s(s^2+1.2s+9)]')
xlabel('Frequency (rad/sec)')
ylabel('Gain dB')

% ********************************************************************
subplot(2, 1, 2)
pmax = 150*ones(1,100); 
pmin = -150*ones(1,100);
semilogx( w, phase, 'o', w, phase, '-', w, pmax, '--', w, pmin, ':')
grid
xlabel('Frequency (rad/sec)')
ylabel('Phase deg')

2 绘制奈奎斯特图（nyquist）

nyquist 图是极坐标图

MATLAB 命令 nyquist 可以计算线性时不变连续系统的频域响应。如果调用时不带左端参数， nyquist 就在屏幕上绘制奈奎斯特图

代码如下：

nyquist(num, den);
nyquist(num,den,w); % 包含了用户指定的频率向量 w 
nyquist(A,B,C,D);
nyquist(A,B,C,D,w);
nyquist(A,B,C,D,iu,w);
nyquist(sys);

使用了上述任一命令，接下来再使用 grid 命令，则不会产生 x-y 网格线（水平和垂直方向的网格线）。如果需要的话可以使用带左端参数的 nyquist 指令，再配合使用 grid 命令来实现。

[re,im,w) = nyquist(num,den);
[re,im,w) = nyquist(num,den,w); 
[re,im,w) = nyquist(A,B,C,D);
[re,im,w) = nyquist(A,B,C,D,w);
[re,im,w) = nyquist(A,B,C,D,iu,w); 
[re,im,w) = nyquist(sys);

MATLAB 将系统的频域响应的数值赋予矩阵 re、im 和 w，但不在屏幕上绘制奈奎斯特图。矩阵 re 和 im 分别为系统在由向量 w 给定的频率点上的频域响应的实部和虚部。应当注意的是，re 和 im 的列数与系统输出的数目相同， 其每一行对应于 w 的一个元素。若要绘制奈奎斯特图， 则可以使用 plot 指令。

举个例子：
$$G(s)=\frac{1}{s^2+0.8s+1}$$
代码如下：

num = [1];
den = [1 0.8 1];
nyquist(num, den)
title('Nyquist Plot of G(s) = 1/(s^2+0.8s+1)')

绘制出图片如下：

如果希望依据自行设定的实轴和虚轴范围绘制奈奎斯特图，例如实轴和虚轴的范围均为从 -2 到 +2，就可以输入命令：

v = [-2 2 -2 2];
axis(v);

注意： 在绘制奈奎斯特图时，如果 MATLAB 运算涉及 “Divided by zero” （被零除），所绘制的奈奎斯特图就可能是错误的，或者不适合进一步分析的需要。

例如：
$$G(s)=\frac{1}{s(s+1)}$$
系统正常绘制出来的图为：

很明显这不利于分析，于是我们限制了坐标范围后 axis([-2 2 -5 5]) 绘制出的图片如下：

添加上 grid 则可以叠印等幅值圆：

3 绘制对数幅相特性图 / 尼柯尔斯图（nichols）

• 尼柯尔斯图（英语：Nichols plot）是将线性非时变系统在不同频率下的增益分贝值及相位绘在一直角坐标系的图上，尼柯尔斯图将二种波德图（波德增益图及波德相位图）结合成一张图，而频率只是曲线中的参数，不直接在图中显示。以系统的对数分贝幅值为纵坐标，以相角或相角裕度为横坐标绘制而成的图形。尼柯尔斯图的命名是来自美国控制工程师尼柯尔斯（Nathaniel B. Nichols）。

• 在伯德图中，$G(jw)$ 的频率响应特性在半对数坐标纸上用两条独立的曲线来表示，即对数幅值曲线和相角曲线。但是，在对数幅相特性图中，伯德图中的这两条曲线合并为一条曲线。通过从伯德图中读取对数幅值和相角的数值，可以很轻松地手工绘制对数幅相特性图。值得注意的是，在对数幅相特性图中绘制 $G(jw)$ 的增益常数变化时仅仅是将曲线向上（增益增加时）或向下（增益减小时）平移，但保持曲线的形状不变。

• 对数幅相特性图的优势在于，它可以快速判断闭环系统的相对稳定性，并很容易设计补偿器。

• 正弦传递函数 $G(jw)$ 和 $1/G(jw)$ 的对数幅相特性图是关于原点斜对称的，这是因为：
  $$|\frac{1}{G(jw)}|indB=-|G(jw)|indB$$
  而且：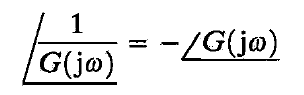

  

4 利用频率特性分析系统的稳定性

4.1 奈奎斯特稳定性分析

奈奎斯特稳定判据：对于图5. 10 所示的系统，如果 开环传递函数 $G(s)H(s)$ 有 $K$ 个极点在右半 $s$ 平面，那么为确保闭环稳定性，当 $s$ 按顺时针方向沿修正的奈奎斯特路径运动时，$G(s)H(s)$ 轨迹必须逆时针包围 $-1+j0$ 点 $K$ 周才能确保闭环稳定性。奈奎斯特路径是由整个虚轴$j\omega$( 从 $\omega =-\infty$ 到 $\omega =\infty$ ) 和右半 $s$ 平面内半径无穷大的半圆所构成的封闭回路。因此，奈奎斯特路径包围了整个右半 $s$ 平面。路径的方向为顺时针方向。修正的奈奎斯特路径也是一种奈奎斯特路径，但它是 在 $jw$ 轴上的极点和零点处采用半径无穷小的半圆路径来避开这些极点和零点后形成的奈奎斯特路径。

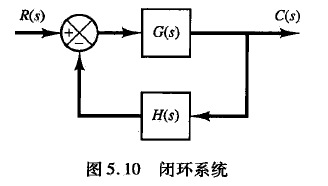
我们可以用MATLAB来表示这个闭环系统（反馈系统）：

sys = feedback(G, H);

当系统为单位反馈系统的时候：

sys = feedback(G, 1);

4.2 关于奈奎斯特稳定判据的几点注解

1. 奈奎斯特稳定判据可记为
   $$Z=N+P$$
   其中 $Z$ 为 $1+G(s)H(s)$ 在右半 $s$ 平面内的零点数目；$N$ 为 $G(s)H(s)$ 轨迹顺时针包围 $ -1 + j0$ 点的周数；$P$ 为 $G(s)H(s)$ 在右半 $s$ 平面内的极点数目。

   如果 $P$ 不为零，则必须要求 $Z=0$ 或 $N=-P$ 才能获得稳定的控制系统。这就意味着 $G(s)H(s)$ 轨迹必须逆时针方向包围 $-1+j0$ 点 $P$ 周。

   如果 $G(s)H(s)$ 不存在位于右半 $s$ 平面的极点，那么 $Z=N$ 。因此，为了得到稳定的系统， $G(jw)H(jw)$ 轨迹不能包围 $-1+j0$ 点 。 在这种情况下， 没有必要考虑对应于整个 $j\omega$ 轴的 $G(jw)H(jw)$ 轨迹，只考虑频率为正的部分即可。该系统的稳定性取决于 $G(jw)H(jw)$ 的奈奎斯特曲线是否包围 $-1+j0$ 点 。奈奎斯特曲线所包围的区域如图 5. 11 所示。为了使系统稳定， $-1+j0$ 点必须位于阴影区域之外。

2. 在判断多环系统的稳定性时必须谨慎，因 为它们可能包含位于右半 $s$ 平面内的极点（注意，尽管系统内环可能不稳定，但整个闭环系统可以通过适当的设计而达到稳定）。简单地观测 $G(jw)H(jw)$ 轨迹是否包围 $-1+j0$ 点不足以发现多环系统的不稳定性。不过，在这种情况下 ，对 $G(s)H(s)$ 的分母运用劳斯稳定判据，很容易判断 $1+G(s)H(s)$ 是否有极点位于右半 $s$ 平面。

   如果像传输迟延环节 $e^{-Ts}$ 这样的超越函数出现在 $G(s)H(s)$ 中，则必须先将它们近似为某个级数展开式，然后再 运用劳斯稳定判据。

3. 如果 $G(jw)H(jw)$ 轨迹穿过 $-1+j0$ 点 ，那么特征方程的零点（即闭环系统的极点）就位于 $jw$ 轴上。这对于实际控制系统而言是不理想的。一个设计合理的闭环控制系统，其特征方程的所有根都不应位于 $jw$ 轴上。

4.3 稳定性分析

下文将举几个示例来演示如何通过奈奎斯特稳定判据进行控制系统的稳定性分析。 ．

如果 $s$ 平面上的奈奎斯特路径包围 $1+G(s)H(s)$ 的 $Z$ 个零点和 $P$ 个极点，但不穿过 $1+G(s)H(s)$ 的任何极点或零点，那么当点 $s$ 沿该路径顺时针方向运动时，$G(s)H(s)$ 平面上的相应映射轨线将顺时针包围 $-1+j0$ 点 $N=Z-P$ 周( $N$ 为负值则表示逆时针方向）。

在使用奈奎斯特稳定判据来判断线性控制系统稳定性时可能发生如下 3 种情况：

1. 不包围 $-1+j0$ 点。这意味着，如果 $G(s)H(s)$ 没有极点位于右半 $s$ 平面，那么系统就是稳定的；否则系统不稳定。

2. 逆时针方向包围 $-1+j0$ 点一周或几周。此时，如果逆时针包围的周数与 $G(s)H(s)$ 右半 $s$ 平面内的极点数相等，则系统稳定；否则系统不稳定。

3. 顺时针包围 $-1+j0$ 点一周或几周。此时系统不稳定。

4.4 相对稳定性

由 Nyquist 稳定判据可知，若系统开环传递函数没有右半平面的极点且闭环系统是稳定的，则开环系统的 Nyquist 曲线离 $(-1,j0)$ 点越远，闭环系统的稳定性越好，反之则越差，这就是通常所说的控制系统相对稳定性，定量为增益裕度和相角裕度

4.5 相角裕度

${\omega }_c$ 称为穿越频率，也称剪切频率或截止频率，

相角裕度是指在增益穿越频率点上，要使系统濒临不稳定边缘所需引入的滞后相角。增益穿越频率是开环传递函数幅值 $|G(jw)H(jw)|=1$ 时的频率。相角裕度 $\gamma$ 是 180°加上开环传递函数在增益穿越频率上的相角 $\varphi$ ，即
$$\gamma =180°+\varphi$$
在极坐标图中，可以从原点到G( j"’) 与单位圆的交点画一条直线。那么，从负实 轴到这条直线的角度即为相角裕度，$\gamma >0$ 时相角裕度为正 ，$\gamma <0$ 时相角裕度为负。对于最小相位系统，当系统稳定时相角裕度必为正。在对数幅相图中，复平面上的临界点对应于 $0dB$ 线和 $-180°$ 线的交点。

4.6 增益裕度

增益裕度是指当开环传递函数 $G(jw)H(jw)$ 的相角为 $-180°$ 时， 幅值 $|G(jw)H(jw)|$ 的倒数。定义相角穿越频率 ${\omega }_1$ 为开环传递函数的相角等于 $-180°$ 时的频率，则可以得到增益裕度。
$$K_g=\frac{1}{|G(j{\omega }_1)H(j{\omega }_1)|}$$
若用分贝数来表示：
$$K_g=-20lg|G(j{\omega }_1)H(j{\omega }_1)|(dB)$$
当增益裕度以分贝数表示时，如果 $K_g>1$ ，则增益裕度为正，如果 $K_g<1$ ，则增益裕度为负。因此，正的增益裕度（以分贝为单位）表明系统稳定，而负的增益裕度表明系统不稳定。

对于稳定的最小相位系统，增益裕度表明增益要增加多少才会使系统变得不稳定。对于不稳定系统，增益裕度表明增益要下降多少才能使系统变得稳定。

4.7 利用幅相频率特性曲线分析系统稳定性

当 $G(jw)H(jw)$ 的开环增益发生变化的时候，曲线仅仅是上下简单平移，而对 $G(jw)H(jw)$ 增加一个恒定相角的时候，曲线为水平平移。

4.8 使用MATLAB获取增益裕度、相角裕度、相角穿越频率、和增益穿越频率

[Gm,Pm,wcp,wcg] =  margin(sys) % 不绘制出bode图

其中 Gm 是增益裕度，Pm 是相角裕度，wcp 是相角穿越频率，wcg 是增益穿越频率

注意 Gm 不是以 dB 为单位

GmdB = 20 * log10(Gm);

margin(num, den) % 传递函数表示形式，计算幅值裕度和相角裕度，并画出bode图
margin(a, b, c, d) % 状态空间表示形式

控制系统工具箱还提供了 allmargin 函数

s  = allmargin(sys); % 计算幅值裕度、相角裕度及对应的频率。针对开环SISO系统而言，输出s是一个结构体
                     % 包括了幅值裕度，相角裕度，以及对应的频率，时滞增益裕度