叉乘
几何图示:
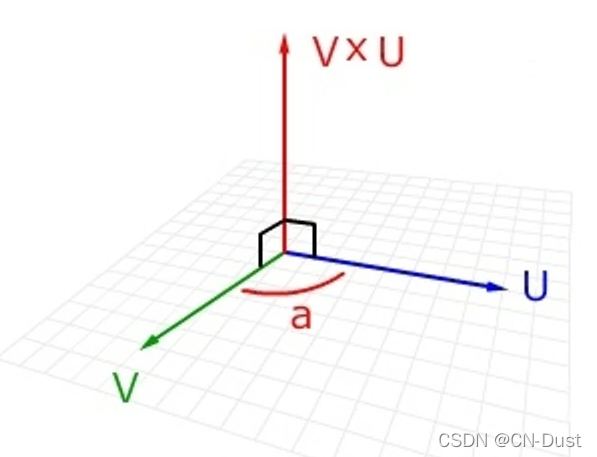
设有
a = ( a x , a y , a z ) , b = ( b x , b y , b z ) \mathbf{a}=\left(a_{x}, a_{y}, a_{z}\right), \mathbf{b}=\left(b_{x}, b_{y}, b_{z}\right) a=(ax,ay,az),b=(bx,by,bz)
i,j,k分别是X,Y,Z轴方向的单位向量,则:
a × b = ( a y b z − a z b y ) i + ( a z b x − a x b z ) j + ( a x b y − a y b x ) k \mathbf{a} \times \mathbf{b}=\left(a_{y} b_{z}-a_{z} b_{y}\right) \mathbf{i}+\left(a_{z} b_{x}-a_{x} b_{z}\right) \mathbf{j}+\left(a_{x} b_{y}-a_{y} b_{x}\right) \mathbf{k} a×b=(aybz−azby)i+(azbx−axbz)j+(axby−aybx)k
为了帮助记忆,利用三阶行列式,写成
∣ i j k a x a y a z b x b y b z ∣ \left|\begin{array}{lll} i & j & k \\ a_{x} & a_{y} & a_{z} \\ b_{x} & b_{y} & b_{z} \end{array}\right| ∣∣∣∣∣∣iaxbxjaybykazbz∣∣∣∣∣∣
设a=(l,m,n),b=(o,p,q),则
a × b = ( l , m , n ) × ( o , p , q ) = ( m q − n p , n o − l q , l p − m o ) \mathbf{a} \times \mathbf{b}=(l, m, n) \times(o, p, q)=(m q-n p, n o-l q, l p-m o) a×b=(l,m,n)×(o,p,q)=(mq−np,no−lq,lp−mo)
利用三阶行列式,写成
∣ i j k l m n o p q ∣ \left|\begin{array}{ccc} i & j & k \\ l & m & n \\ o & p & q \end{array}\right| ∣∣∣∣∣∣ilojmpknq∣∣∣∣∣∣
推导
设有三个单位向量i,j,k,则:
i → = ( 1 , 0 , 0 ) j → = ( 0 , 1 , 0 ) k → = ( 0 , 0 , 1 ) \begin{aligned} &\overrightarrow{\mathrm{i}}=(1,0,0) \\ &\overrightarrow{\mathrm{j}}=(0,1,0) \\ &\overrightarrow{\mathrm{k}}=(0,0,1) \end{aligned} i=(1,0,0)j=(0,1,0)k=(0,0,1)
且
i → = j → × k → j → = k → × i → k → = i → × j → k → × j → = − i → i → × k → = − j → j → × i → = − k → i → × i → = j → × j → = k → × k → = 0 → = 0 \overrightarrow{\mathrm{i}}=\overrightarrow{\mathrm{j}} \times \overrightarrow{\mathrm{k}}\\ \overrightarrow{\mathrm{j}}=\overrightarrow{\mathrm{k}} \times \overrightarrow{\mathrm{i}}\\ \overrightarrow{\mathrm{k}}=\overrightarrow{\mathrm{i}} \times \overrightarrow{\mathrm{j}}\\ \overrightarrow{\mathrm{k}} \times \overrightarrow{\mathrm{j}}=- \overrightarrow{\mathrm{i}}\\ \overrightarrow{\mathrm{i}} \times \overrightarrow{\mathrm{k}}=- \overrightarrow{\mathrm{j}}\\ \overrightarrow{\mathrm{j}} \times \overrightarrow{\mathrm{i}}=- \overrightarrow{\mathrm{k}}\\ \overrightarrow{\mathrm{i}} \times \overrightarrow{\mathrm{i}} = \overrightarrow{\mathrm{j}} \times \overrightarrow{\mathrm{j}} = \overrightarrow{\mathrm{k}} \times \overrightarrow{\mathrm{k}} = \overrightarrow{\mathrm{0}} = 0 i=j×kj=k×ik=i×jk×j=−ii×k=−jj×i=−ki×i=j×j=k×k=0=0
i,j,k是三个相互垂直的向量。它们刚好可以构成一个坐标系。
对于处于i,j,k构成的坐标系中的向量u,v我们可以如下表示:
u → = ( x u , y u , z u ) v → = ( x v , y v , z v ) \begin{aligned} &\overrightarrow{\mathrm{u}}=\left(\mathrm{x}_{\mathrm{u}}, \mathrm{y}_{\mathrm{u}}, \mathrm{z}_{\mathrm{u}}\right) \\ &\overrightarrow{\mathrm{v}}=\left(\mathrm{x}_{\mathrm{v}}, \mathrm{y}_{\mathrm{v}}, \mathrm{z}_{\mathrm{v}}\right) \end{aligned} u=(xu,yu,zu)v=(xv,yv,zv)
u → = X u ⋅ i → + y u ⋅ j → + z u ⋅ k → v → = X v ⋅ i → + y v ⋅ j → + z v ⋅ k → \begin{aligned} &\overrightarrow{\mathrm{u}}=\mathrm{X}_{\mathrm{u}} \cdot \overrightarrow{\mathrm{i}}+\mathrm{y}_{\mathrm{u}} \cdot \overrightarrow{\mathrm{j}}+\mathrm{z}_{\mathrm{u}} \cdot \overrightarrow{\mathrm{k}} \\ &\overrightarrow{\mathrm{v}}=\mathrm{X}_{\mathrm{v}} \cdot \overrightarrow{\mathrm{i}}+\mathrm{y}_{\mathrm{v}} \cdot \overrightarrow{\mathrm{j}}+\mathrm{z}_{\mathrm{v}} \cdot \overrightarrow{\mathrm{k}} \end{aligned} u=Xu⋅i+yu⋅j+zu⋅kv=Xv⋅i+yv⋅j+zv⋅k
u → × v → = ( x u ⋅ i → + y u ⋅ j → + z u ⋅ k → ) × ( x v ⋅ i → + y v j → + z v ⋅ k → ) \overrightarrow{\mathrm{u}} \times \overrightarrow{\mathrm{v}}=\left(\mathrm{x}_{\mathrm{u}} \cdot \overrightarrow{\mathrm{i}}+\mathrm{y}_{\mathrm{u}} \cdot \overrightarrow{\mathrm{j}}+\mathrm{z}_{\mathrm{u}} \cdot \overrightarrow{\mathrm{k}}\right) \times\left(\mathrm{x}_{\mathrm{v}} \cdot \overrightarrow{\mathrm{i}}+\mathrm{y}_{\mathrm{v}} \overrightarrow{\mathrm{j}}+\mathrm{z}_{\mathrm{v}} \cdot \overrightarrow{\mathrm{k}}\right) u×v=(xu⋅i+yu⋅j+zu⋅k)×(xv⋅i+yvj+zv⋅k)
展开,得:
u → × v → = x u ⋅ x v ⋅ ( i → ⋅ i → ) + x u ⋅ y v ⋅ ( i → ⋅ j → ) + x u ⋅ z v ⋅ ( i → ⋅ k → ) + y u ⋅ x v ⋅ ( j → ⋅ i → ) + y u ⋅ y v ⋅ ( j → ⋅ j → ) + y u ⋅ z v ⋅ ( j → ⋅ k → ) + z u ⋅ x v ⋅ ( k → ⋅ i → ) + z u ⋅ y v ⋅ ( k → ⋅ j → ) + z u ⋅ z v ⋅ ( k → ⋅ k → ) \begin{aligned} \overrightarrow{\mathrm{u}} \times \overrightarrow{\mathrm{v}}=& \mathrm{x}_{\mathrm{u}} \cdot \mathrm{x}_{\mathrm{v}} \cdot(\overrightarrow{\mathrm{i}} \cdot \overrightarrow{\mathrm{i}})+\mathrm{x}_{\mathrm{u}} \cdot \mathrm{y}_{\mathrm{v}} \cdot(\overrightarrow{\mathrm{i}} \cdot \overrightarrow{\mathrm{j}})+\mathrm{x}_{\mathrm{u}} \cdot \mathrm{z}_{\mathrm{v}} \cdot(\overrightarrow{\mathrm{i}} \cdot \overrightarrow{\mathrm{k}}) \\ &+\mathrm{y}_{\mathrm{u}} \cdot \mathrm{x}_{\mathrm{v}} \cdot(\overrightarrow{\mathrm{j}} \cdot \overrightarrow{\mathrm{i}})+\mathrm{y}_{\mathrm{u}} \cdot \mathrm{y}_{\mathrm{v}} \cdot(\overrightarrow{\mathrm{j}} \cdot \overrightarrow{\mathrm{j}})+\mathrm{y}_{\mathrm{u}} \cdot \mathrm{z}_{\mathrm{v}} \cdot(\overrightarrow{\mathrm{j}} \cdot \overrightarrow{\mathrm{k}}) \\ &+\mathrm{z}_{\mathrm{u}} \cdot \mathrm{x}_{\mathrm{v}} \cdot(\overrightarrow{\mathrm{k}} \cdot \overrightarrow{\mathrm{i}})+\mathrm{z}_{\mathrm{u}} \cdot \mathrm{y}_{\mathrm{v}} \cdot(\overrightarrow{\mathrm{k}} \cdot \overrightarrow{\mathrm{j}})+\mathrm{z}_{\mathrm{u}} \cdot \mathrm{z}_{\mathrm{v}} \cdot(\overrightarrow{\mathrm{k}} \cdot \overrightarrow{\mathrm{k}}) \end{aligned} u×v=xu⋅xv⋅(i⋅i)+xu⋅yv⋅(i⋅j)+xu⋅zv⋅(i⋅k)+yu⋅xv⋅(j⋅i)+yu⋅yv⋅(j⋅j)+yu⋅zv⋅(j⋅k)+zu⋅xv⋅(k⋅i)+zu⋅yv⋅(k⋅j)+zu⋅zv⋅(k⋅k)
化简,得:
u ⃗ × v ⃗ = 0 → + x u ⋅ y v ⋅ ( k ⃗ ) + x u ⋅ z v ⋅ ( − j ⃗ ) + y u ⋅ x v ⋅ ( − k ⃗ ) + 0 → + y u ⋅ z v ⋅ ( i ⃗ ) + z u ⋅ x V ⋅ ( j ⃗ ) + z u ⋅ y v ⋅ ( − i ⃗ ) + 0 → \begin{gathered} \vec{u} \times \vec{v}=\overrightarrow{0}+x_{u} \cdot y_{v} \cdot(\vec{k})+x_{u} \cdot z_{v} \cdot(-\vec{j}) \\ +y_{u} \cdot x_{v} \cdot(-\vec{k})+\overrightarrow{0}+y_{u} \cdot z_{v} \cdot(\vec{i}) \\ +z_{u} \cdot x_{V} \cdot(\vec{j})+z_{u} \cdot y_{v} \cdot(-\vec{i})+\overrightarrow{0} \end{gathered} u×v=0+xu⋅yv⋅(k)+xu⋅zv⋅(−j)+yu⋅xv⋅(−k)+0+yu⋅zv⋅(i)+zu⋅xV⋅(j)+zu⋅yv⋅(−i)+0
合并,得:
u → × v → = ( y u ⋅ z v − z u ⋅ y v ) ⋅ ( i → ) + ( z u ⋅ x v − x u ⋅ z v ) ⋅ ( j → ) + ( x u ⋅ y v − y u ⋅ x v ) ⋅ ( k → ) \overrightarrow{\mathrm{u}} \times \overrightarrow{\mathrm{v}}=\left(\mathrm{y}_{\mathrm{u}} \cdot \mathrm{z}_{\mathrm{v}}-\mathrm{z}_{\mathrm{u}} \cdot \mathrm{y}_{\mathrm{v}}\right) \cdot(\overrightarrow{\mathrm{i}})+\left(\mathrm{z}_{\mathrm{u}} \cdot \mathrm{x}_{\mathrm{v}}-\mathrm{x}_{\mathrm{u}} \cdot \mathrm{z}_{\mathrm{v}}\right) \cdot(\overrightarrow{\mathrm{j}})+\left(\mathrm{x}_{\mathrm{u}} \cdot \mathrm{y}_{\mathrm{v}}-\mathrm{y}_{\mathrm{u}} \cdot \mathrm{x}_{\mathrm{v}}\right) \cdot(\overrightarrow{\mathrm{k}}) u×v=(yu⋅zv−zu⋅yv)⋅(i)+(zu⋅xv−xu⋅zv)⋅(j)+(xu⋅yv−yu⋅xv)⋅(k)
叉乘的几何意义
设
c → = a → × b → \overrightarrow{\mathrm{c}}=\overrightarrow{\mathrm{a}} \times \overrightarrow{\mathrm{b}} c=a×b
则c的方向垂直于a与b所决定的平面,c的指向按右手定则从a转向b来确定。
且c的长度在数值上等于以a,b,夹角为θ组成的平行四边形的面积。
∣ c ∣ = ∣ a ∣ ∣ b ∣ ⋅ sin θ |c|=|a||b|·\sin \theta ∣c∣=∣a∣∣b∣⋅sinθ
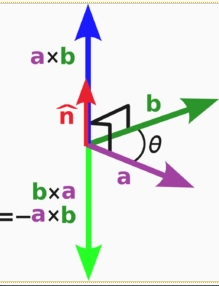
右手定则:
若坐标系是满足右手定则的,当右手的四指从a以不超过180度的转角转向b时,竖起的大拇指指向是c的方向。
代数规则
-
反交换律
a → × b → = − b → × a → \overrightarrow{\mathrm{a}} \times \overrightarrow{\mathrm{b}}=-\overrightarrow{\mathrm{b}} \times \overrightarrow{\mathrm{a}} a×b=−b×a -
加法的分配律
a ⃗ × ( b ⃗ + c ⃗ ) = a ⃗ × b ⃗ + a ⃗ × c ⃗ \vec{a} \times(\vec{b}+\vec{c})=\vec{a} \times \vec{b}+\vec{a} \times \vec{c} a×(b+c)=a×b+a×c
-
与标量乘法兼容
r a → × b → = a → × r b → = r × ( a → × b → ) r\overrightarrow{\mathrm{a}} \times \overrightarrow{\mathrm{b}}=\overrightarrow{\mathrm{a}} \times r\overrightarrow{\mathrm{b}}=r \times(\overrightarrow{\mathrm{a}} \times \overrightarrow{\mathrm{b}}) ra×b=a×rb=r×(a×b) -
不满足结合律,但满足雅可比恒等式
a → × ( b → × c → ) + b → × ( c → × a → ) + c → × ( a → × b → ) = 0 \overrightarrow{\mathrm{a}} \times(\overrightarrow{\mathrm{b}} \times \overrightarrow{\mathrm{c}})+\overrightarrow{\mathrm{b}} \times(\overrightarrow{\mathrm{c}} \times \overrightarrow{\mathrm{a}})+\overrightarrow{\mathrm{c}} \times(\overrightarrow{\mathrm{a}} \times \overrightarrow{\mathrm{b}}) = 0 a×(b×c)+b×(c×a)+c×(a×b)=0 -
分配律,线性性和雅可比恒等式别表明:具有向量加法和叉积的R3构成了一个李代数。
-
两个非零向量a和b平行,当且仅当
a×b=0。
拉格朗日公式
设向量坐标 a ⃗ = ( x 1 , y 1 , z 1 ) , b ⃗ = ( x 2 , y 2 , z 2 ) , c ⃗ = ( x 3 , y 3 , z 3 ) \vec{a}=(x 1, y 1, z 1), \vec{b}=(x 2, y 2, z 2), \vec{c}=(x 3, y 3, z 3) a=(x1,y1,z1),b=(x2,y2,z2),c=(x3,y3,z3), 则
( a ⃗ × b ⃗ ) × c ⃗ = ( y 1 z 2 − z 1 y 2 , z 1 x 2 − x 1 z 2 , x 1 y 2 − x 2 y 1 ) × ( x 3 , y 3 , z 3 ) = ( z 1 z 3 x 2 − x 1 z 2 z 3 − x 1 y 2 y 3 + x 2 y 1 y 3 , x 1 x 3 y 2 − x 2 x 3 y 1 − y 1 z 2 z 3 + z 1 z 3 y 2 , y 1 y 3 z 2 − y 2 y 3 z 1 − x 2 x 3 z 1 + x 1 x 3 z 2 ) = ( x 2 ( x 1 x 3 + y 1 y 3 + z 1 z 3 ) , y 2 ( x 1 x 3 + y 1 y 3 + z 1 z 3 ) , z 2 ( x 1 x 3 + y 1 y 3 + z 1 z 3 ) ) − ( x 1 ( x 2 x 3 + y 2 y 3 + z 2 z 3 ) , y 1 ( x 2 x 3 + y 2 y 3 + z 2 z 3 ) , z 1 ( x 2 x 3 + y 2 y 3 + z 2 z 3 ) ) = ( x 2 ( a ⃗ ⋅ c ⃗ ) , y 2 ( a ⃗ ⋅ c ⃗ ) , z 2 ( a ⃗ ⋅ c ⃗ ) ) − ( x 1 ( b ⃗ ⋅ c ⃗ ) , y 1 ( b ⃗ ⋅ c ⃗ ) , z 1 ( b ⃗ ⋅ c ⃗ ) ) = b ⃗ ( a ⃗ ⋅ c ⃗ ) − a ⃗ ( b ⃗ ⋅ c ⃗ ) \begin{aligned} &(\vec{a} \times \vec{b}) \times \vec{c}=\left(y_{1} z_{2}-z_{1} y_{2}, z_{1} x_{2}-x_{1} z_{2}, x_{1} y_{2}-x_{2} y_{1}\right) \times\left(x_{3}, y_{3}, z_{3}\right) \\ &=\left(z_{1} z_{3} x_{2}-x_{1} z_{2} z_{3}-x_{1} y_{2} y_{3}+x_{2} y_{1} y_{3}, x_{1} x_{3} y_{2}-x_{2} x_{3} y_{1}\right. \\ &\left.-y_{1} z_{2} z_{3}+z_{1} z_{3} y_{2}, y_{1} y_{3} z_{2}-y_{2} y_{3} z_{1}-x_{2} x_{3} z_{1}+x_{1} x_{3} z_{2}\right) \\ &=\left(x_{2}\left(x_{1} x_{3}+y_{1} y_{3}+z_{1} z_{3}\right), y_{2}\left(x_{1} x_{3}+y_{1} y_{3}+z_{1} z_{3}\right), z_{2}\left(x_{1} x_{3}+y_{1} y_{3}+z_{1} z_{3}\right)\right) \\ &-\left(x_{1}\left(x_{2} x_{3}+y_{2} y_{3}+z_{2} z_{3}\right), y_{1}\left(x_{2} x_{3}+y_{2} y_{3}+z_{2} z_{3}\right), z_{1}\left(x_{2} x_{3}+y_{2} y_{3}+z_{2} z_{3}\right)\right) \\ &=\left(x_{2}(\vec{a} \cdot \vec{c}), y_{2}(\vec{a} \cdot \vec{c}), z_{2}(\vec{a} \cdot \vec{c})\right)-\left(x_{1}(\vec{b} \cdot \vec{c}), y_{1}(\vec{b} \cdot \vec{c}), z_{1}(\vec{b} \cdot \vec{c})\right) \\ &=\vec{b}(\vec{a} \cdot \vec{c})-\vec{a}(\vec{b} \cdot \vec{c}) \end{aligned} (a×b)×c=(y1z2−z1y2,z1x2−x1z2,x1y2−x2y1)×(x3,y3,z3)=(z1z3x2−x1z2z3−x1y2y3+x2y1y3,x1x3y2−x2x3y1−y1z2z3+z1z3y2,y1y3z2−y2y3z1−x2x3z1+x1x3z2)=(x2(x1x3+y1y3+z1z3),y2(x1x3+y1y3+z1z3),z2(x1x3+y1y3+z1z3))−(x1(x2x3+y2y3+z2z3),y1(x2x3+y2y3+z2z3),z1(x2x3+y2y3+z2z3))=(x2(a⋅c),y2(a⋅c),z2(a⋅c))−(x1(b⋅c),y1(b⋅c),z1(b⋅c))=b(a⋅c)−a(b⋅c)
这就是二重向量叉乘化简公式 ( a ⃗ × b ⃗ ) × c ⃗ = b ⃗ ( a ⃗ ⋅ c ⃗ ) − a ⃗ ( b ⃗ ⋅ c ⃗ ) (\vec{a} \times \vec{b}) \times \vec{c}=\vec{b}(\vec{a} \cdot \vec{c})-\vec{a}(\vec{b} \cdot \vec{c}) (a×b)×c=b(a⋅c)−a(b⋅c)
转化一下,得
a ⃗ × ( b ⃗ × c ⃗ ) = b ⃗ ( a ⃗ ⋅ c ⃗ ) − c ⃗ ( a ⃗ ⋅ b ⃗ ) \vec{a} \times (\vec{b} \times \vec{c})=\vec{b}(\vec{a} \cdot \vec{c})-\vec{c}(\vec{a} \cdot \vec{b}) a×(b×c)=b(a⋅c)−c(a⋅b)
向量积(矢积)与数量积(标积)的区别
