理解 word2vec

本文是个人对 word2vec 的理解，绝大部分翻译自 Xin Rong 博士的 paper，同时参考了网上很多blogs，都列在References中了。
注：文中数学公式，不加粗小写代表标量值，加粗小写代表向量，加粗大写代表矩阵。

1. word2vec 简介

Word2Vec是Google在2013 年开源的一个词向量（Word Embedding）计算工具，其用来解决单词的分布编码问题。它通过从大量文本预料中以无监督方式学习语义知识型，被广泛地应用于自然语言处理中。

2. 什么是 word embedding（词嵌入）

我们知道，文本是一种非结构化的数据信息，如汉字是一种方块字，是不可以直接被计算的。因此需要将这种非结构化的信息转换为结构化的信息，从而实现针对文本信息进行计算。简单来说，就是把文字转换成数学向量。

这种表示方法很多，常见的有如下三种：

• 独热编码 | one-hot representation
• 整数编码
• 词嵌入 | word embedding

所谓独热码就是开一个和词汇表大小相同的向量，向量的一个位置就代表了一个单词，例如，假设单词表中只有四个单词，我、爱、中、国，那么一个可能的编码为：

我：[1 0 0 0]
爱：[0 1 0 0]
中：[0 0 1 0]
国：[0 0 0 1]

但是在实际情况中，文本中很可能出现成千上万个不同的词，这时候向量就会非常长。其中99%以上都是 0，导致所谓的维度灾难。

整数编码更简单，就是用一个整数代表一个词，如1代表我，2代表爱，等等。

整数编码的缺点如下：

• 无法表达词语之间的关系
• 对于模型解释而言，整数编码可能具有挑战性。

word embedding 则是文本表示的一类方法。他可以将文本通过一个低维向量来表达，不像 one-hot 那么长。并且语意相似的词在向量空间上也会比较相近。而Word2vec则是一种基于统计方法来获得词嵌入的方法，2013年由谷歌的 Mikolov 提出。

Word2vec 算法有2种训练模式（2 种网络结构，CBOW和Skip-Gram）：

1. CBOW(Continuous Bag-of-Word Model)：用单词的上下文预测当前单词
2. Skip-gram：当前词预测其上下文

首先要说明，word2vec 本质上是一个神经网络，其输入是 单词的 one-hot 向量，输出是待预测单词的 one-hot 向量（并不是所谓的word embedding），而单词的真正的词嵌入表示是蕴含在在网络的参数中的。

下面分别写一下自己的理解，其中大部分都是来自 Xin Rong 博士在论文 word2vec Parameter Learning Explained 中所解释的。

3. CBOW

CBOW 是用上下文预测当前的单词，也就是输入是多个上下文的单词，输出为待预测的一个单词。首先，为了简便，我们将输入的上下文单词设置为一个。

3. 1 One-word context

此时模型输入一个单词，预测一个单词。下图显示了网络的结构：

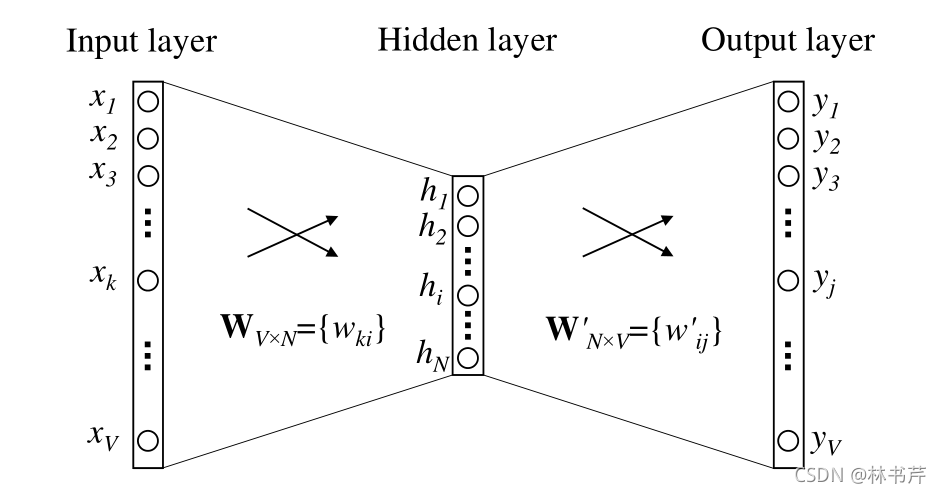
其实网络结构很简单，图中就只有一个隐藏层，且隐藏层没有激活函数，输出层有Softmax函数，即输出预测单词的概率分布，概率大的就被预测出来了。我们假设，单词表的长度为 $V$，即一共有 $V$ 个单词。隐藏层的节点数为 $N$，输出层的节点数和输入层一样也是 $V$，因为就是要输出每个单词出现的概率，而真值就是该被预测的单词的one-hot，那么整个网络就是要训练成，输出尽可能接近待预测单词的one-hot。

输入层和隐藏层之间为全连接网络，由于没有激活函数，其输入输出关系很简单：
$$\mathbf{h}={\mathbf{W}}^T\mathbf{x}={\mathbf{v}}_I^T$$
其中，$\mathbf{x}$ 是一个 $V\times 1$ 的列向量。$\mathbf{W}$ 是一个 $V\times N$ 矩阵，那么 $\mathbf{h}$ 就是一个 $N\times 1$ 的列向量。由于 $\mathbf{x}$ 只有一个元素为 $1$ ，假设是第 $k$ 维为1，其他都为 $0$，那么这个操作的本质是把 $\mathbf{W}$ 的第 $k$ 行转置之后复制给 $\mathbf{h}$，即 ${\mathbf{v}}_I^T$，下标 $I$ 代表 input。

同理，隐藏层和输出层之间通过一个大小为 $N\times V$ 的矩阵 ${\mathbf{W}}^{\prime }$ 全连接（${\mathbf{W}}^{\prime }$ 和 $\mathbf{W}$ 没有任何关系！），设其输出为 $\mathbf{u}$，那么输出的第 $j$ 个元素为：
$$u_j={{\mathbf{v}}_j^{\prime }}^T\mathbf{h}$$
其中，${{\mathbf{v}}_j^{\prime }}^T$ 代表矩阵 ${{\mathbf{W}}^{\prime }}^T$ 的第 $j$ 行（或者说，矩阵 ${\mathbf{W}}^{\prime }$ 的第 $j$ 列 ）。最后使用 Softmax 获得单词的后验概率（这里所有的概率之和加起来就等于 $1$ 了）：
$$p\left(w_j\mid w_I\right)=y_j=\frac{\exp \left(u_j\right)}{{\sum }_{j^{\prime }=1}^V\exp \left(u_{j^{\prime }}\right)}$$
$p\left(w_j\mid w_I\right)$ 代表给定输入单词，预测输出第 $j$ 个单词的概率。代入 $u_j$，有，
$$p\left(w_j\mid w_I\right)=\frac{\exp \left({\mathbf{v}}_j^{\prime }{\mathbf{v}}_I\right)}{{\sum }_{j^{\prime }=1}^V\exp \left({\mathbf{v}}_{j^{\prime }}^{\prime }{}^T{\mathbf{v}}_I\right)}$$
我们假设预测真值出现在第 $j^{\ast }$ 个位置，则预测输出应该是 ${\mathbf{t}}_{j^{\ast }}$ 是一个 one-hot向量，并且只在第 $j^{\ast }$ 个位置有一个 $1$，其他位置都是 $0$，那么，我们目的是想让 输出 $\mathbf{y}$ 的第 $j^{\ast }$ 个位置的值越大越好（尽可能接近 ${\mathbf{t}}_{j^{\ast }}$ ），其他位置的值越小越好，
$$\begin{array}{rl}\max p\left(w_O\mid w_I\right)& =\max y_{j^{\ast }}\\ & =\max \log y_{j^{\ast }}\\ & =u_{j^{\ast }}-\log \sum _{j^{\prime }=1}^V\exp \left(u_{j^{\prime }}\right):=-E,\end{array}$$
其中，$E=-\log p\left(w_O\mid w_I\right)$ 是损失函数，要使得上述的概率最大，那就是最小化 $E$。
因此，对上式进行反向传播即可更新参数如下，
$$\begin{gathered} \frac{\partial E}{\partial w_{ij}^{\prime }}=\frac{\partial E}{\partial u_j}\cdot \frac{\partial u_j}{\partial w_{ij}^{\prime }}=(y_j-t_j)\cdot h_i \\ {{\mathbf{v}}_j^{\prime }}^{\text{(new)}}={{\mathbf{v}}_j^{\prime }}^{\text{ (old)}}-\eta \cdot (y_j-t_j)\cdot \mathbf{h}\text{ for }j=1,2,\cdots ,V \end{gathered}$$

$y_j,t_j,h_i$ 分别代表向量 $\mathbf{y},\mathbf{t},\mathbf{h}$ 的第 $j,j,i$ 个元素，$w_{ij}$ 代表矩阵 ${\mathbf{W}}^{\prime }$ 第 $i$ 行第 $j$ 列元素，$\eta$ 是学习率。
同理，更新 $\mathbf{W}$ 过程如下，我们首先求 $E$ 对 $h_i$ 的导数如下：
$$\frac{\partial E}{\partial h_i}=\sum _{j=1}^V\frac{\partial E}{\partial u_j}\cdot \frac{\partial u_j}{\partial h_i}=\sum _{j=1}^V(y_j-t_j)\cdot w_{ij}^{\prime }:={\mathrm{E}\mathrm{H}}_i$$

$:=$ 表示记为。

参数定义同上。下一步就可以算出 $E$ 对 $W$ 的偏导数，这里要注意，因为input layer的操作是，$\mathbf{W}$ 的第 $k$ 行转置之后复制给 $\mathbf{h}$，也就是说，$h_i=w_{ki}$，其中的 $k$ 代表输入 one-hot 向量的第 $k$ 个元素是 $1$，其他都是 $0$，因此我们更新 $\mathbf{W}$ 的时候只要更新第 $k$ 行，其他的值由于梯度是 $0$，保持不变：
$$\frac{\partial E}{\partial w_{ki}}=\frac{\partial E}{\partial h_i}\cdot \frac{\partial h_i}{\partial w_{ki}}=\sum _{j=1}^V(y_j-t_j)\cdot w_{ij}^{\prime }={\mathrm{E}\mathrm{H}}_i\cdot x_k\text{for }w\text{ is a constant, }i=1,2,\cdots ,N$$
向量形式表示更新如下：
$${\mathbf{v}}_I^{(\text{new })}={\mathbf{v}}_I^{\text{(old) }}-\eta {\mathrm{E}\mathrm{H}}^T$$
同样也是只更新 $\mathbf{W}$ 的第$k$ 行，其他行保持不变。

3.2 Multi-word context

现在我们把模型拓展到有多个上下文单词输入的情况，下图显示了一个 Multi-word context 的 CBOW 模型，

此时，在计算隐藏层输出时，CBOW 模型不直接复制输入上下文的输入向量，而是取输入上下文向量的平均值，并使用输入到隐藏层权值矩阵的乘积的平均向量作为输出：
$$\begin{array}{rl}\mathbf{h}& =\frac{1}{C}{\mathbf{W}}^T\left({\mathbf{x}}_1+{\mathbf{x}}_2+\cdots +{\mathbf{x}}_C\right)\\ & =\frac{1}{C}{\left({\mathbf{v}}_{w_1}+{\mathbf{v}}_{w_2}+\cdots +{\mathbf{v}}_{w_C}\right)}^T\end{array}$$
其中，$C$ 是上下文单词的数量（在 One-word context 中，$C=1$），$w_1,\cdots ,w_C$ 是上下文的单词向量，${\mathbf{v}}_1,\cdots ,{\mathbf{v}}_C$ 同上。损失函数定义如下：
$$\begin{array}{rl}E& =-\log p\left(w_O\mid w_{I,1},\cdots ,w_{I,C}\right)\\ & =-u_{j^{\ast }}+\log \sum _{j^{\prime }=1}^V\exp \left(u_{j^{\prime }}\right)\\ & =-{\mathbf{v}}_O^{\prime }\cdot \mathbf{h}+\log \sum _{j^{\prime }=1}^V\exp \left({\mathbf{v}}_j^{\prime }{}^T\cdot \mathbf{h}\right)\end{array}$$
由于隐藏层到输出向量部分没有改变，因此 ${\mathbf{W}}^{\prime }$ 的更新和之前一样：
$${{\mathbf{v}}_j^{\prime }}^{\text{(new)}}={{\mathbf{v}}_j^{\prime }}^{\text{ (old)}}-\eta \cdot (y_j-t_j)\cdot \mathbf{h}\text{ for }j=1,2,\cdots ,V$$
$\mathbf{W}$ 的更新其实也差不多，只不过我们需要对上下文中的每个单词 $w_{I,c}$ 应用以下等式：
$${\mathbf{v}}_{I,c}^{(\mathrm{n}\mathrm{e}\mathrm{w})}={\mathbf{v}}_{I,c}^{(\text{old })}-\frac{1}{C}\cdot \eta \cdot {\mathrm{E}\mathrm{H}}^T\text{ for }c=1,2,\cdots ,C$$
其中，${\mathbf{v}}_{I,c}$ 是输入上下文中第 $c$ 个单词的输入向量，或者说，对应矩阵 $\mathbf{W}$ 的第 $k_c$ 行，其中 $k_c$ 为输入第 $c$ 个单词在 one-hot 编码中不为 $0$ 的那一维。

如，上下文单词中，第一个单词 $c=1$ 为"我"，$V=4$，编码为 $[1000]$，那么，$k_1=0$；上下文单词中，第二个单词 $c=2$ 为"国"，$V=4$，编码为 $[0001]$，那么，$k_2=3$。

4. Skip-Gram Model

下图显示了 Skip-Gram Model 结构：

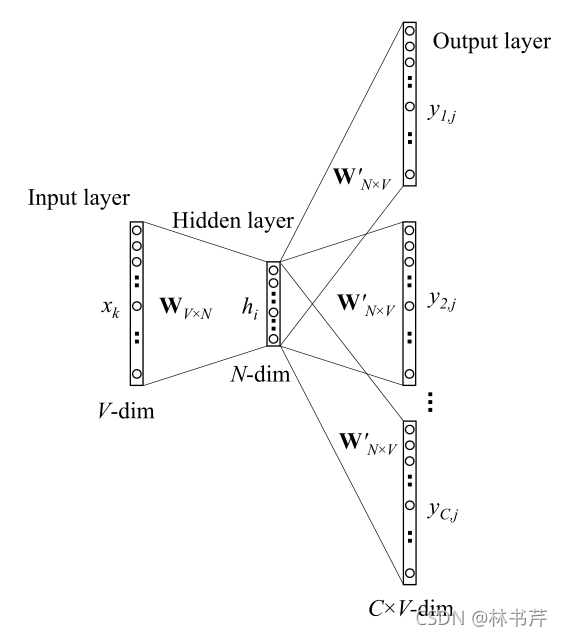
Skip-Gram Model 的参数更新方程的推导与one-word-context model 没有太大区别。损失函数变成了：
$$\begin{array}{rl}E& =-\log p\left(w_{O,1},w_{O,2},\cdots ,w_{O,C}\mid w_I\right)\\ & =-\log \prod _{c=1}^C\frac{\exp \left(u_{c,j_c^{\ast }}\right)}{{\sum }_{j^{\prime }=1}^V\exp \left(u_{j^{\prime }}\right)}\\ & =-\sum _{c=1}^C{u}_{j_c^{\ast }}+C\cdot \log \sum _{j^{\prime }=1}^V\exp \left(u_{j^{\prime }}\right)\end{array}$$
由于 Skip-Gram Model 是给定一个输入单词，预测其上下文多个单词的概率，所以损失函数变成 $p\left(w_{O,1},w_{O,2},\cdots ,w_{O,C}\mid w_I\right)$ 的负对数。其中，$j_c^{\ast }$ 是词汇表中第 $c$ 个上下文输出单词在 one-hot 编码中不为 $0$ 的那一维（解释同上）。

由于有多个输出，我们求损失 $E$ 对每个输出向量的每个维度的偏导如下：
$$\frac{\partial E}{\partial u_{c,j}}=y_{c,j}-t_{c,j}:=e_{c,j}$$

$:=$ 是将 $y_{c,j}-t_{c,j}$ 记为 $e_{c,j}$

为了表示简便，我们再记：
$${\mathrm{E}\mathrm{I}}_j=\sum _{c=1}^C{e}_{c,j}$$
和前面一样，$c$ 代表输出上下文的个数。下一步求 $E$ 对 ${\mathbf{W}}^{\prime }$ 中元素的偏导数，并更新：
$$\frac{\partial E}{\partial w_{ij}^{\prime }}=\sum _{c=1}^C\frac{\partial E}{\partial u_{c,j}}\cdot \frac{\partial u_{c,j}}{\partial w_{ij}^{\prime }}={\mathrm{E}\mathrm{I}}_j\cdot h_i$$
则更新如下：
$$w_{ij}^{\prime }(\text{ new })=w_{ij}^{\prime }\text{ (old) }-\eta \cdot {\mathrm{E}\mathrm{I}}_j\cdot h_i$$
或者向量形式表示：
$${\mathbf{v}}_j^{\prime }\text{ (new) }={\mathbf{v}}_j^{\prime }\text{ (old) }-\eta \cdot {\mathrm{E}\mathrm{I}}_j\cdot \mathbf{h}\text{ for }j=1,2,\cdots ,V$$
可以看出，除了损失函数，其他的和 one-word-context model 几乎没有区别。

最后求输入层到隐藏层的权值矩阵的更新方程。由于从结构上可以看出，他和 one-word-context model 完全一样，所以我们直接给出更新方程如下：
$${\mathbf{v}}_I^{(\text{new })}={\mathbf{v}}_I^{(\text{old })}-\eta \cdot {\mathrm{E}\mathrm{H}}^T$$
其中，$EH$ 是一个 $n$ 维向量，向量中的每一个元素为：
$${\mathrm{E}\mathrm{H}}_i=\sum _{j=1}^V{\mathrm{E}\mathrm{I}}_j\cdot w_{ij}^{\prime }$$

5. 最后

我们观察公式：
$${{\mathbf{v}}_j^{\prime }}^{\text{(new)}}={{\mathbf{v}}_j^{\prime }}^{\text{ (old)}}-\eta \cdot (y_j-t_j)\cdot \mathbf{h}\text{ for }j=1,2,\cdots ,V$$
word2vec 在更新过程中需要变量一边词汇表中的所有的单词，对于每一步的更新，我们还要计算 $w_j,u_j,y_j,e_j$ 最终才能更新一个 ${\mathbf{v}}_j^{\prime }$，计算量可想而知。所有在实际的 word2vec 中，使用了很多 tricks 优化计算效率，具体不再展开，推荐 References 中的博客和这一篇博客。

References

1. https://easyai.tech/ai-definition/word-embedding/#wordembedding
2. word2vec Parameter Learning Explained
3. https://mp.weixin.qq.com/s/7dsjfcOfm9uPheJrmB0Ghw