信号处理频域特征

频域特征指标及其MATLAB代码实现（重心频率、均方频率、均方根频率、频率方差、频率标准差）

% max ：最大值
% min ：最小值
% mean ：平均值
% peak ：峰峰值
% arv ：整流平均值
% var ：方差
% std ：标准差
% kurtosis ：峭度
% skewness ：偏度
% rms ：均方根
% waveformF ：波形因子
% peakF ：峰值因子
% impulseF ：脉冲因子
% clearanceF：裕度因子
% FC：重心频率
% MSF：均方频率
% RMSF：均方根频率
% VF：频率方差
% RVF：频率标准差
% SKMean：谱峭度的均值
% SKStd：谱峭度的标准差
% SKSkewness：谱峭度的偏度
% SKKurtosis：谱峭度的峭度

1. 能量

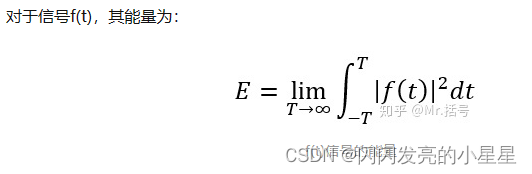
2. 功率

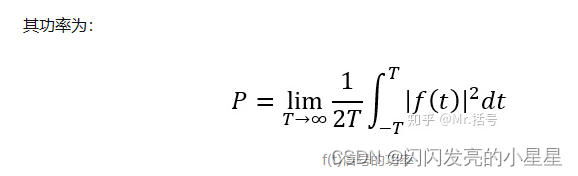
能量就是信号的平方在区间(-∞,+∞)上的积分。

功率就是能量与“无穷长的时间”的比值。（该表达不严谨，只辅助理解）

频谱

一般来说，频谱分析指的是将信号做傅里叶变换从而进行分析。频谱分析是包括幅频谱和相频谱两张图的。不过最常用的是幅频谱。

频谱matlab 实现

频谱用到的函数主要是fft和fftshift。

需要注意的主要有三点：

1.直接做fft的结果，信号的前半部分对应频率[0,fs/2]，后半部分对应[-fs/2,0]。参见频谱结果图的第2张。为了将零频点移到频谱中间，需要使用fftshift函数，结果参见频谱结果图的第3张。

2.通常我们关心的都是正频率区间的结果，有两种截取方法，一种是在fftshift的结果中截后半段，一种是在fft的结果中截前半段，其结果是一样的。后一种方法更简洁。具体参见频谱结果图的第4、5张。

3.根据奈奎斯特定理，信号的采样频率（1/t_s）必须大于信号频率最大值的两倍。

频域特征值提取的MATLAB代码实现（频谱、功率谱、倒频谱）

频谱python 实现

DFT DFS DIFT FFT 的关系

学过卷积，我们都知道有时域卷积定理和频域卷积定理，在这里只需要记住两点：1.在一个域的相乘等于另一个域的卷积；2.与脉冲函数的卷积

能量谱

能量谱也叫能量谱密度，能量谱密度描述了信号或时间序列的能量如何随频率分布。能量谱是原信号傅立叶变换的平方。

功率谱

功率谱是功率谱密度函数（PSD）的简称，它定义为单位频带内的信号功率。

功率谱是针对功率信号来说的。功率谱的推导公式相对复杂，不过幸运的是维纳-辛钦定理证明了：一段信号的功率谱等于这段信号自相关函数的傅里叶变换。

所以求功率谱就有了两种方法：1.(傅立叶变换的平方)/(区间长度)；2.自相关函数的傅里叶变换。这两种方法分别叫做直接法和相关函数法。

功率谱这里存在着一些问题，整理如下：

1.功率谱密度的单位是什么，看有的写的是dB，还有的说是W/Hz。

功率谱的单位是W/Hz，单位是dB时是做了对数处理（10logX）。取对数的目的是使那些振幅较低的成分相对高振幅成分得以拉高，以便观察掩盖在低幅噪声中的周期信号。

2.求功率谱的两种方法有什么区别么？

从原理上讲似乎没什么区别，从MATLAB仿真结果上来看，相关函数法对噪声的抑制效果更好，图线更平滑。

3.FFT和PSD都是表示的频谱特性，帮助我们找出峰值的位置，那么有了FFT为什么还要提出PSD？

信号分为确定信号和随机信号，而确定信号又分为能量信号和功率信号，随机信号一定是功率信号。根据狄里赫利条件，能量信号可以直接进行傅里叶变换，而功率信号不行。对于无法做傅里叶变换的信号，只能走一步弯路，先求自相关，再做傅里叶。但是物理意义上就是功率谱了。不过总之得到了信号的频率特性。

4.既然为什么随机信号的一次FFT没有意义却还能(傅立叶变换的平方)/(区间长度)得到功率谱？

对随机信号直接做FFT的做法其实就是截断成能量信号进行处理，这种处理不符合随机信号定义，但之所以这样做，是做短时频域分析下作的近似处理。（这里希望能有大神能给出更好的解释）

所以总结，频谱和能量谱（也叫能量谱密度）是傅里叶变换得到的复数结果和模平方的关系； 而功率谱（也就是功率谱密度）是针对随机信号分析提出的概念。

倒频谱

倒频谱（Cepstrum）也叫倒谱、二次谱和对数功率谱等。倒频谱的工程型定义是：信号功率谱对数值进行傅立叶逆变换的结果。（信号→求功率谱→求对数→求傅里叶逆变换）

为什么叫倒频？

为什么翻译作倒频谱呢？个人的理解是，频谱（功率谱）反应的频率特征点横坐标是频率f（Hz），在倒频谱中对应的特征点的横坐标是时间t（s），而f与t互为倒数。从这里也可以看出，虽然倒频谱也叫“频谱”，其横坐标却并不是频率，而是时间。

倒频有什么好处呢？

“该分析方法方便提取、分析原频谱图上肉眼难以识别的周期性信号，能将原来频谱图上成族的边频带谱线简化为单根谱线，受传感器的测点位置及传输途径的影响小。”
ps: 这里的周期信号，指重复出现的边频带。
1.方便提取、分析原频谱图上肉眼难以识别的周期性信号

我们知道，频谱分析就是为了提取原始信号中的周期性信号的，怎么频谱中的信号还会有周期性？这就又涉及到两个概念：调制和边频带。

调制分为幅值调制和频率调制。下面以齿轮的幅值调制为例进行说明：齿轮的振动信号主要包括两部分，分别是齿轮啮合振动信号（高频）和齿轮轴的转频振动信号（低频），时域和频域曲线分别如下图所示：

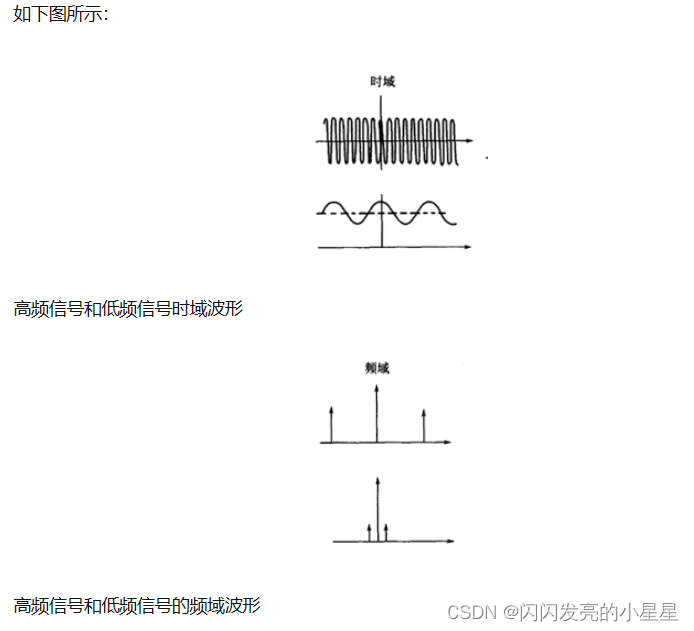
调制就是高低频率信号的混合。幅值调制从数学上看，相当于两个信号在时域上相乘；而在频域上，相当于两个信号的卷积。调制后的信号在时域和频域上分别变为：

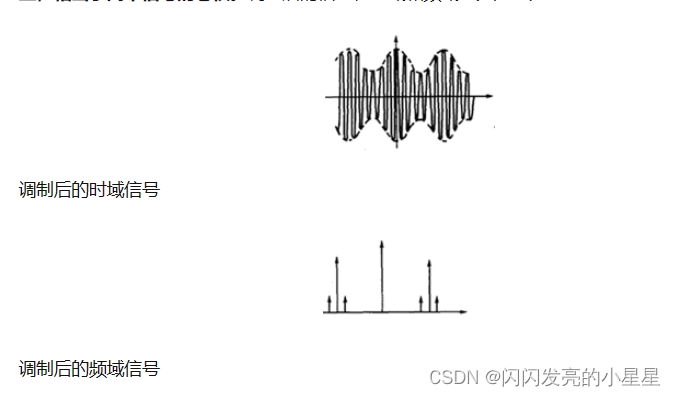
我们发现，调制后的信号中，除原来的啮合频率分量外，增加了一对分量，它们是以高频信号特征频率为中心，对称分布于两侧，所以称为边频带。

实际实验中齿轮啮合振动信号（高频）和齿轮轴的转频振动信号（低频）的特征频率可能是有多组的，其调制后的频域信号近似于一组频率间隔较大的脉冲函数和一组频率间隔较小的脉冲函数的卷积，从而在频谱上形成若干组围绕啮合频率及其倍频成分两侧的边频族，如下图：

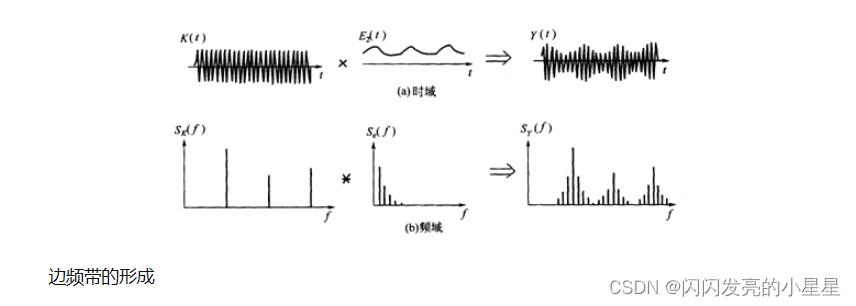
边频带的形成

说了一大堆，终于回归到上边提到的问题：倒频谱“方便提取、分析原频谱图上肉眼难以识别的周期性信号”。这里指的周期性信号，就是重复出现的边频带。

倒频谱能较好地检测出功率谱上的周期成分，通常在功率谱上无法对边频的总体水平作出定量估计，而倒频谱对边频成分具有“概括”能力，能较明显地显示出功率谱上的周期成分，将原来谱上成族的边频带谱线简化为单根谱线，便于观察，而齿轮发生故障时的振动频谱具有的边频带一般都具有等间隔（故障频率）的结构，利用倒频谱这个优点，可以检测出功率谱中难以辨识的周期性信号。
2.受传感器的测点位置及传输途径的影响小

这是倒频谱的第二个好处。对于布置在不同位置的传感器，由于传递路径不同，其功率谱也不相同。但在倒频谱上，由于信号源的振动效应和传递途径的效应分离开来，代表齿轮振动特征的倒频率分量几乎完全相同，只是低倒频率段存在由于传递函数差异而产生的影响。在进行倒频谱分析时，可以不必考虑信号测取时的衰减和标定系数所带来的影响。这一优点对于故障识别极为有用。

关于倒频谱，文章 齿轮故障诊断常用信号分析处理方法 给出了具体了例子，方便理解。

matlab 实现

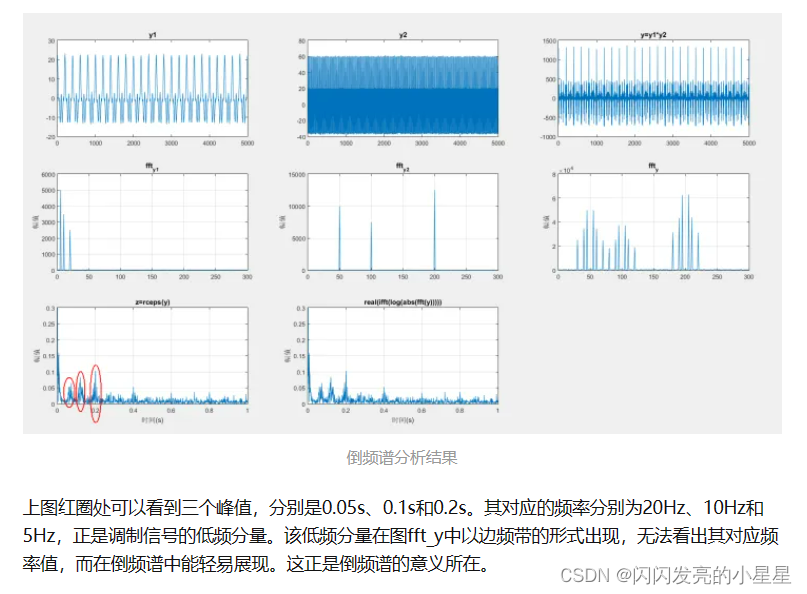
倒频谱的求解函数为rceps（实倒频谱），在MATLAB的帮助文档中，rceps的计算公式为real(ifft(log(abs(fft(y)))))，即信号→频谱→对数→傅里叶逆变换，而倒频谱的定义表述中却是信号→功率谱→对数→傅里叶逆变换。即功率谱被换成了频谱。私以为是因为功率谱为频谱值的平方，在取对数后平方会变成系数2，对后续计算影响不大，因而可以近似认为结果相同。

sf = 1000;
nfft = 1000;
x = 0:1/sf:5;
y1=10*cos(2*pi*5*x)+7*cos(2*pi*10*x)+5*cos(2*pi*20*x)+0.5*randn(size(x));
y2=20*cos(2*pi*50*x)+15*cos(2*pi*100*x)+25*cos(2*pi*200*x)+0.5*randn(size(x));
for i = 1:length(x)
    y(i) = y1(i)*y2(i);
end
subplot(3,3,1)
plot(y1);xlim([0 5000]);title('y1');
subplot(3,3,2)
plot(y2);xlim([0 5000]);title('y2');
subplot(3,3,3)
plot(y);xlim([0 5000]);title('y=y1*y2');

t = 0:1/sf:(nfft-1)/sf;
nn = 1:nfft;
subplot(3,3,4)
ft = fft(y1,nfft);
Y = abs(ft);
plot(0:nfft/2-1,((Y(1:nfft/2))));
title('fft_y_1');
ylabel('幅值');xlim([0 300]);
grid on;
subplot(3,3,5)
ft = fft(y2,nfft);
Y = abs(ft);
plot(0:nfft/2-1,((Y(1:nfft/2))));
title('fft_y_2');
ylabel('幅值');xlim([0 300]);
grid on;
subplot(3,3,6)
ft = fft(y,nfft);
Y = abs(ft);
plot(0:nfft/2-1,((Y(1:nfft/2))));
title('fft_y');
ylabel('幅值');xlim([0 300]);
grid on;

subplot(3,3,7)
z = rceps(y);
plot(t(nn),abs(z(nn)));
title('z=rceps(y)');ylim([0 0.3]);
xlabel('时间(s)');
ylabel('幅值');
grid on;
subplot(3,3,8)
yy = real(ifft(log(abs(fft(y))))); %信号→傅里叶→对数→傅里叶逆变换
plot(t(nn),abs(yy(nn)));
title('real(ifft(log(abs(fft(y)))))');ylim([0 0.3]);
xlabel('时间(s)');
ylabel('幅值');
grid on;

小波分析

参考：https://zhuanlan.zhihu.com/p/34989414

重心频率

重心频率能够描述信号在频谱中分量较大的信号成分的频率，反映信号功率谱的分布情况。换句话说，对于给定的频带范围，低于重心频率的频率范围内包含的能量是信号总能量的一半。

另一种理解方式，重心频率是以功率谱的幅值为权值的加权平均，所以重心频率会向功率谱幅值更大（即权值更大）的位置移动。

更形象一点，如果把下图中功率谱曲线围起来的区域看作一块木板，那么当把这块木板放在重心频率虚线所在的钢丝上时，木板刚好能保持平衡。

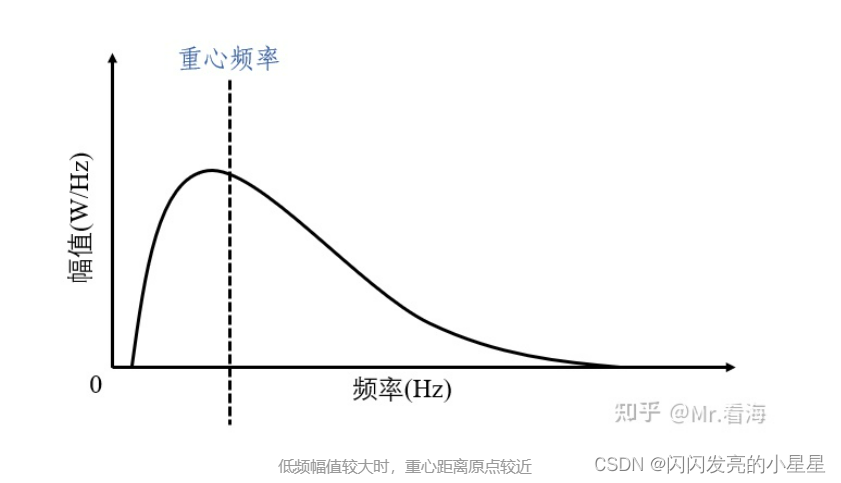
低频幅值较大时，重心距离原点较近

重心频率、均方频率、均方根频率都是描述功率谱主频带位置分布的。