数字信号处理四：离散时间信号与系统的频域分析

一、信号变换概述

信号是数字信号处理领域中最基本、最重要的概念。而数字信号变换技术，又是对信号进行处理操作的最基本、最有效的途径之一。因此，数字信号变换技术，便成为数字信号处理领域中专业人员所必须要掌握的一项最基本的技能。
简单的说，数字信号变换技术就是为了处理和操作上的方便和可能，通过数学变换，将一个域内的信号变换映射到另一个域内的信号的方法。常用的数字信号变换主要有：傅里叶变换（DTFT）、离散傅里叶变换（DFT）、Z变换（ZT）等。这些变换，都有着各自的理论和其应用背景。

二、傅里叶变换

傅里叶变换是信号分析和处理的重要工具。有限长序列作为离散信号的一种，在数字信号处理中占有着极其重要的位置。对于有限长序列，离散傅里叶变换不仅在理论上有着重要的意义，而且有快速计算的方法——快速傅里叶变换。所以在各种数字信号处理的运算方法中，越来越起到核心的作用。

2.1 傅里叶变换的几种形式

1) 非周期连续时间信号的傅里叶变换

非周期连续时间信号x(t)的傅里叶变换 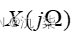可以表示为:

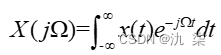
逆变换为:

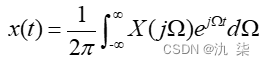
在这里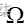， 是模拟角频率。可以看到，时域的连续函数造成频域的非周期谱，时域的非周期性造成频域的连续谱。
结论：非周期连续时间函数对应于一非周期连续频域变换函数。

2) 周期连续时间信号的傅里叶变换

周期为T的周期性连续时间信号x(t)的傅里叶变换是离散频域函数，可表示为

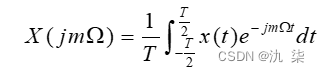
逆变换为

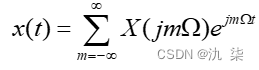
这就是经常称之为傅里叶级数的变换形式。在这里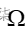， 也是模拟角频率。可以看到，时域的连续函数造成频率域的非周期谱，频域函数的离散造成时域函数的周期性。
结论：周期连续时间函数对应于一非周期离散频域变换函数。

3) 非周期离散时间信号的傅里叶变换

非周期离散时间信号x(n)的傅里叶变换 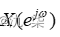可以表示为:

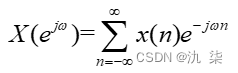
逆变换为:

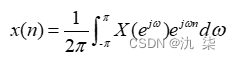
在这里， w是数字频率，它和模拟角频率的关系为 。可以看到，时域的取样对应于频域的周期延拓，而时域函数的非周期性造成频域的离散谱。
结论：非周期离散时间函数对应于一周期连续频域变换函数。

4) 周期离散时间信号的傅里叶变换

周期离散时间信号 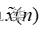的傅里叶变换——离散傅里叶级数，可以表示为:

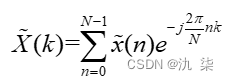
逆变换为:

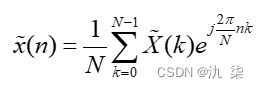
可以看到，时域的取样对应于频域的周期延拓，而时域函数的周期性造成频域的离散谱。
结论：周期离散时间函数对应于一周期离散频域变换函数。

2.2 离散傅里叶变换（DFT）

离散傅里叶级数是周期序列，仍不便于计算机计算。但离散傅里叶级数虽是周期序列，却只有N个独立的数值，所以它的许多特性可以通过有限长序列延拓来得到。对于一个长度为N的有限长序列x(n)，也即x(n)只在n=0~(N-1)个点上有非零值，其余的值皆为零，即

把序列x(n)以N为周期进行周期延拓得到周期序列 ，则有

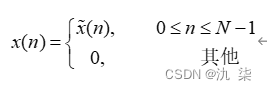
所以，有限长序列x(n)的离散傅里叶变换（DFT）为

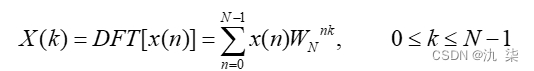
逆变换为

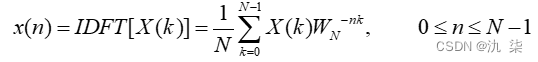
2.3 快速傅里叶变换（FFT）

在信号处理中，DFT的计算具有举足轻重的地位，信号的相关、滤波、谱估计等都要通过DFT来实现。然而，当N很大的时候，求一个N点的DFT要完成NN次复数乘法和N(N-1)次复数加法，其计算量相当大。1965年J.W.Cooley和J.W.Tukey巧妙地利用 因子的周期性和对称性，构造了一个DFT快速算法，即快速傅里叶变换(FFT)的概念。
快速傅里叶变换并不是与DFT不同的另外一种变换，而是为减少DFT计算次数的一种快速有效的算法。这种快速算法，主要是利用 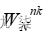的周期性、对称性和可约性，不断的把长序列的DFT分解成几个短序列的DFT，从而减少运算次数。最简单最常用的算法是基2FFT。
基2FFT算法分为两类，即按时间抽取（Decimation－In－Time，简称DIT-FFT）法和按频率抽取（Decimation－In－Frequency，简称DIF-FFT）法。
为了计算数据的快速傅里叶变换，在numpy库的fft模块中提供了一系列丰富的数学函数，主要有fft、ifft、fft2 、ifft2和fftshift、ifftshift等。当所处理的数据的长度为2的幂次时，采用基-2算法进行计算，计算速度会显著增加。所以，要尽可能使所要处理的数据长度为2的幂次或者用补零的方式使之成为2的幂次。

三、离散时间LTI系统的频率响应特性分析

对于因果稳定的离散时间系统，系统的频率响应定义为：

其中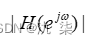， 称为离散时间系统的幅频特性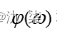； 称为离散时间系统的相频特性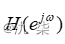； 是以2π为周期的周期函数。因此，只要分析 范围内的情况，便可分析出系统的整个频率特性。
在scipy库的signal模块中提供了一个求离散时间系统频响特性的函数dfreqresp，

语句格式：
w, H = signal.dfreqresp(sys,whole=False)
其中返回值w包含 范围内的N个频率等分点；
返回值H则是离散时间系统频率响应 范围内N个频率处的值。此函数的另一种调用格式为：
w, H = signal.dfreqresp(sys,whole=True)
与第一种方式不同之处在于角频率的范围由 扩展到了 。

函数调用时用到的参数sys代表系统，可用scipy库中的函数signal.TransferFunction实现.

语句格式为：
sys = signal.TransferFunction(b, a,dt)
其中的b与a分别表示 的分子和分母多项式（均按z的正幂次排列，最后一项为常数项）的系数向量。dt为采样时间。

绘制系统 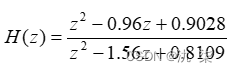的频率响应曲线。
程序代码示例如下：

from scipy import signal
import matplotlib.pyplot as plt
import numpy as np

b=[1,-0.96,0.9028]
a=[1,-1.56,0.8109]
sys = signal.TransferFunction(b, a,dt=0.05)
w, H = signal.dfreqresp(sys,whole=True)

plt.figure(figsize=(15,15))
plt.subplot(211)
plt.plot(w, np.abs(H), "b")
plt.xlabel('ω(rad/s)')
plt.ylabel('Magnitude')
plt.title('|H(e^jw)|')
plt.grid('on')

plt.subplot(212)
plt.plot(w, np.angle(H), "r")
plt.xlabel('ω(rad/s)')
plt.ylabel('Phase')
plt.title('φ(w)')
plt.grid('on')
plt.show()

程序运行结果如下:
。

已知 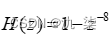，绘制系统的幅频特性和相频特性曲线。程序代码示例如下：

from scipy import signal
import matplotlib.pyplot as plt
import numpy as np

b=[1,0,0,0,0,0,0,0,-1]
a=[1,0,0,0,0,0,0,0,0]
sys = signal.TransferFunction(b,a,dt=0.05)
w, H = signal.dfreqresp(sys,whole=True)

plt.figure(figsize=(12,12))
plt.subplot(211)
plt.plot(w, np.abs(H), "b")
plt.xlabel('ω(rad/s)')
plt.ylabel('Magnitude')
plt.title('|H(e^jw)|')
plt.grid('on')

plt.subplot(212)
plt.plot(w, np.angle(H), "r")
plt.xlabel('ω(rad/s)')
plt.ylabel('Phase')
plt.title('φ(w)')
plt.grid('on')
plt.show()

程序运行结果如图下。

应用数字信号处理三学过的函数，我们可以画出此系统函数的零极点分布图，如下。

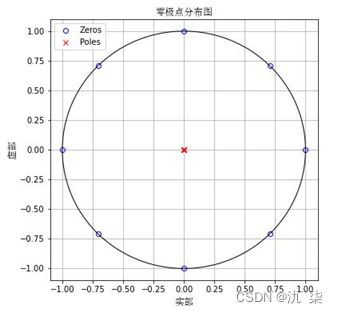
从图中可以看出，系统有8个零点，均匀的分布在单位圆上，有1个8阶极点，在原点处。此系统称为梳状滤波器。
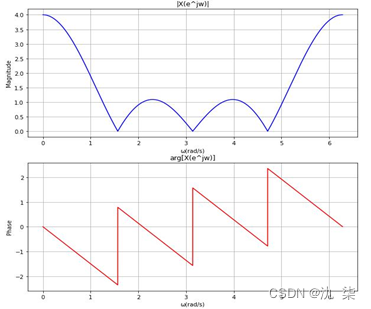
已知 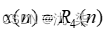，其傅里叶变换为 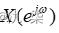，绘制其幅度谱和相位谱。

程序代码示例如下：

from scipy import signal
import matplotlib.pyplot as plt
import numpy as np

b=[1,0,0,0,-1]
a=[1,-1,0,0,0]
sys = signal.TransferFunction(b,a,dt=0.05)
w, H = signal.dfreqresp(sys,whole=True)
plt.figure(figsize=(10,10))
plt.subplot(211)
plt.plot(w, np.abs(H), "b")
plt.xlabel('ω(rad/s)')
plt.ylabel('Magnitude')
plt.title('|X(e^jw)|')
plt.grid('on')

plt.subplot(212)
plt.plot(w, np.angle(H), "r")
plt.xlabel('ω(rad/s)')
plt.ylabel('Phase')
plt.title('arg[X(e^jw)]')
plt.grid('on')
plt.show()

程序运行结果如下图所示。

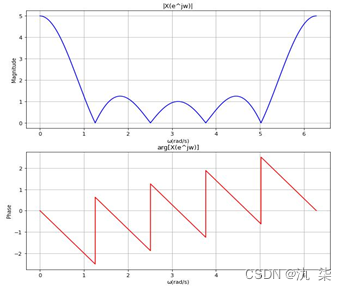
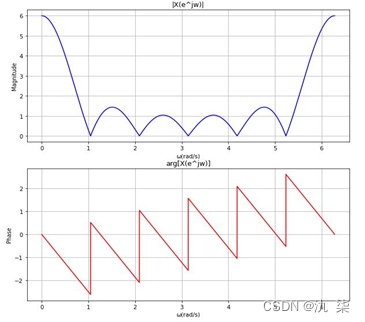
按照同样的方法，我们可以得到 R5(n)、R6(n)的幅度谱和相位谱，如下图所示。

四、DFT的计算

对长度为M的有限长序列 做N点DFT（ N>=M），可以直接调用numpy库中fft模块里面的函数fft，ifft，如果N等于2的整数次幂，可以应用FFT快速算法计算。

求DFT正变换用到的函数为fft，调用格式如下：np.fft.fft(x)，其中x为时间域的序列。求DFT逆变换用到的函数为ifft，调用格式如下：np.fft.ifft(X)，其中X为频率域的频谱值。

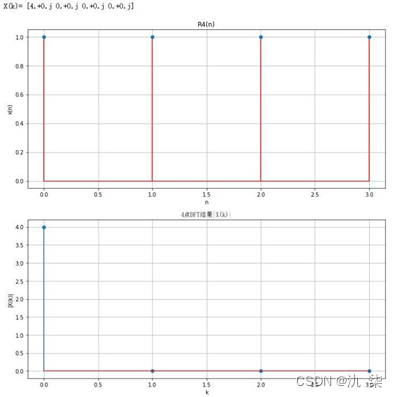
已知 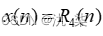，求 (n)的4点和8点DFT，并绘制幅度谱。
程序代码示例如下：

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.font_manager import FontProperties

font_set = FontProperties(fname=r"c:\windows\fonts\simsun.ttc", size=12)
N=4     # DFT的长度
x=[1,1,1,1]
N1=len(x)        # 序列x(n)的原始长度
xn=np.zeros(N)
xn[0:N1]=x        # 通过补零，使得x(n)的长度等于N

XK = np.fft.fft(xn)   # 计算FFT
print('X(k)=',XK)    # 打印DFT的结果
n=np.arange(N)
k=np.arange(N)

plt.figure(figsize=(12,12))
plt.subplot(211)
plt.stem(n,xn, "r")
plt.xlabel('n')
plt.ylabel('x(n)')
plt.title('R4(n)')
plt.grid('on')

plt.subplot(212)
plt.stem(k,np.abs(XK))
plt.xlabel('k')
plt.ylabel('|X(k)|')
plt.title('4点DFT结果|X(k)|',fontproperties=font_set)
plt.grid('on')
plt.show()

程序运行结果如下图所示。

将程序中N的值改为8，可得8点DFT的结果，如下图所示。

如果要求x(n)的L点DFT，只需将程序中N的值改为相应的数值即可。
已知 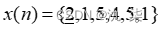，求x(n)的6点DFT结果X(k)。
程序代码示例如下：

import numpy as np
xn=[2,1,5,4,5,1]
XK = np.fft.fft(xn)      #计算6点DFT
print(XK)

程序运行结果为：[18.+0.j -6.+0.j 0.+0.j 6.+0.j 0.+0.j -6.+0.j]

从结果可知，
在这个例题中，由于 是实数序列，且满足偶对称，所以X(k)也是实数，且偶对称。
已知 ，求X(k)的6点IDFT结果 。
程序代码示例如下：

import numpy as np
XK=[18,-6,0,6,0,-6]
xn = np.fft.ifft(XK) #计算6点IDFT
print(xn)

程序运行结果为：[2.+0.j 1.+0.j 5.+0.j 4.+0.j 5.+0.j 1.+0.j]

从结果可知， ，和上题的结果一致。
在上面的例题中，我们得到的频谱是关于N/2点对称的，为了将频域数据中的直流成
分（即频率为0处的值）移到频谱的中间位置，可以应用函数np.fft.fftshift，调用格式为：np.fft.fftshift(XK)。
对平移以后的频谱，在做逆傅里叶变换回到时间域之前，必须先把频谱再平移回去，用到的函数为np.fft.ifftshift，调用格式为：np.fft.ifftshift(XK)。
已知 ，求x(n)的6点DFT结果X(k)，并将频域的直流成分移到频谱的中间。
程序代码示例如下：

import numpy as np
xn=[2,1,5,4,5,1]
XK = np.fft.fft(xn)  #计算6点DFT
XK_shift=np.fft.fftshift(XK)
print(XK)
print(XK_shift)

程序运行结果为：
[18.+0.j -6.+0.j 0.+0.j 6.+0.j 0.+0.j -6.+0.j]
[ 6.+0.j 0.+0.j -6.+0.j 18.+0.j -6.+0.j 0.+0.j]

五、DFT与DTFT的关系

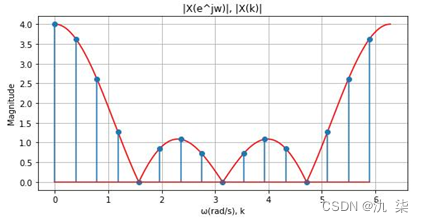
x(n)的N点DFT，为 的DTFT在区间[0，2π]上的N点等间隔采样。下面通过例题来验证一下。

已知 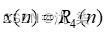，其傅里叶变换为 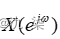，绘制其DTFT的幅度谱及N点DFT的幅度谱。（N分别取8，16，32，64，128）
当N=8时，程序代码示例如下：

from scipy import signal
import matplotlib.pyplot as plt
import numpy as np

b=[1,0,0,0,-1]
a=[1,-1,0,0,0]
sys = signal.TransferFunction(b,a,dt=0.05)
w, H = signal.dfreqresp(sys,whole=True)
N=8               # DFT的长度
x1=[1,1,1,1]
N1=len(x1)
x=np.zeros(N)
x[0:N1]=x1
n1=np.arange(N)
n=(2*np.pi)/N
k=n*n1
XK = np.fft.fft(x)    #计算FFT
plt.figure(figsize=(8,4))

plt.plot(w, np.abs(H), "r")
plt.xlabel('ω(rad/s), k')
plt.ylabel('Magnitude')
plt.title('|X(e^jw)|, |X(k)|')
plt.grid('on')
plt.stem(k,np.abs(XK))
plt.show()

程序运行结果如下图所示。

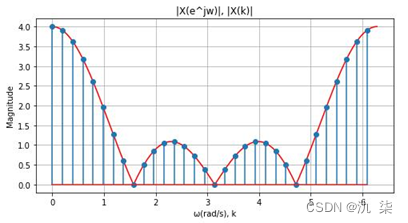
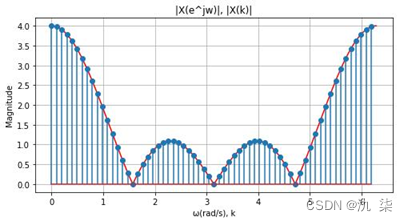
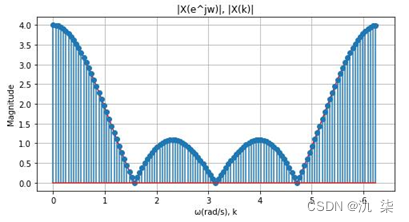
当N分别取16，32，64，128时，结果如下图所示。