数字信号处理——有限长离散变换

1 正交变换

令x[n]表示长度为N的时域序列，X[k]表示其N点正交变换的系数。正交变换的一般形式如下：
$$\begin{gathered} X[k]=\sum _{n=0}^{N-1}x[n]{\Psi }^{\ast }[k,n],0⩽k⩽N-1 \\ x[n]=\frac{1}{N}\sum _{k=0}^{N-1}X[k]\Psi [k,n],0⩽n⩽N-1 \end{gathered}$$
通常前者称为分析式，后者称为综合式。$\Psi [k,n]$为基序列应该满足条件：
$$\frac{1}{N}\sum _{n=0}^{N-1}\Psi [k,n]{\Psi }^{\ast }[k,n]=\{\begin{array}{c}1,l=k\\ 0,l\ne k\end{array}$$

2 离散傅里叶变换

2.1 定义

• 长度为N 的有限长序列x[n]的DTFT 为：
  $$X(e^{j\omega })=\sum _{n=0}^{N-1}x[n]e^{-j\omega [k]n}$$

• 对频谱进行离散化操作，即对$\omega$在[0, 2π)范围的频率均匀采样：
  $$\omega [k]=\frac{2\pi k}{N},k=0,1,\cdots ,N-1$$

• 经过采样，DTFT中$e^{-j\omega n}$的第k 个样本变成
  $$e^{-j\omega [k]n}=e^{-j\frac{2\pi kn}{N}}$$

• 因此，DTFT$e^{-j\omega n}$的第k个样本变成（定义记号$W_N=e^{-j\frac{2\pi }{N}}$):
  $$X_N[k]=X(e^{j\omega [k]})=\sum _{n=0}^{N-1}x[n]W_N^{kn}$$

• 离散时间信号x[n] 的N 点离散傅里叶变换(DFT)：
  $$X[K]=\sum _{n=0}^{N-1}$$

• DFT 序列X[k] 的N 点离散傅里叶逆变换(IDFT) ：
  $$x[n]=\frac{1}{N}\sum _{k=0}^{N-1}X[k]W_N^{-kn},0⩽n⩽N-1$$

2.2 DFT矩阵形式

DFT可用矩阵的形式表示：
$$X=D_{N}x$$
其中，X是由N个DFT样本组成的向量
$$X={\left[\begin{array}{cccc}X[0]& X[1]& \cdots & X[N-1]\end{array}\right]}^T$$
x是N个输入样本的向量
$$x={\left[\begin{array}{cccc}x[0]& x[1]& \cdots & x[N-1]\end{array}\right]}^T$$
$D_N$是大小为N*N的DFT矩阵$$|B|=\left[\begin{array}{ccccc}1& 1& 1& \cdots & 1\\ 1& W_N^1& W_N^2& \cdots & W_N^{N-1}\\ 1& W_N^2& W_N^4& \cdots & W_N^{2(N-1)}\\ ⋮& ⋮& ⋮& \cdots & ⋮\\ 1& W_N^{N-1}& W_N^{2(N-1)}& \cdots & W_N^{(N-1)(N-1)}\end{array}\right]$$

2.3 MATLAB计算DFT

1. DFT 矩阵DN 可以通过调用dftmtx(N) 函数来获得，它的求逆形式可以通过conj(
   dftmtx(N))/N 得到，然后通过矩阵相乘计算DFT；
2. DFT 和IDFT 在MATLAB 中通常通过调用fft 和ifft 来获得，这更加高效便捷；
3. fftshift 用于移位DFT，以确保频谱中间点为零频。

3 DTFT与DFT及其逆之间的关系

3.1 与离散时间傅里叶变换的关系

长度为N的序列x[n]的N点DFT序列X[k]就是其傅里叶变换$X(e^{j\omega })$在N个等间隔频率${\omega }_k=2\pi k/N$上的一组频率样本。
即：

• 通过插值将DFT变为DTFT
• 通过采样将DTFT变为DFT

3.2 用DFT对DTFT进行数值计算

通过对序列进行补零，使其长度为2的整数次方，就可以使用FFT快速算法。

4 圆周卷积

定义：
$$y_C[n]=\sum _{m=0}^{N-1}g[m]h[<n-m>N]$$
和线性卷积一样圆周卷积满足交换律和结合律。

5 有限长序列的分类

5.1 根据共轭对称分类:

• 循环共轭对称序列(circular conjugate-symmetric sequence)

• 循环共轭反对称序列(circular conjugate-antisymmetric sequence)

• 一个N点DFTX[k]在满足以下情况时被称为循环共轭对称序列：
  $$X[k]=X^{\ast }[<-k{>}_N]=X^{\ast }[<N-k{>}_N]$$

  • 实部为循环偶对称
  • 虚部为循环奇对称

• 一个N点DFT X[k]在满足以下情况时被称为循环共轭反对称序列：
  $$X[k]=-X^{\ast }[<-k{>}_N]=-X^{\ast }[<N-k{>}_N]$$

  • 实部为循环奇对称
  • 虚部为循环偶对称

一个复序列DFT X[k]可以表示为一个循环共轭对称部分$X_{cs}[k]$和一个循环共轭反对称部分$X_{ca}[k]$的和：
$$X[k]=X_{cs}[k]+X_{ca}[k],0⩽k⩽N-1$$
其中：
$$\begin{gathered} X_{cs}[k]=\frac{1}{2}(X[k]+X^{\ast }[<-k{>}_N]),0⩽k⩽N-1 \\ {X}_{ca}[k]=\frac{1}{2}(X[k]-X^{\ast }[<-k{>}_N]),0⩽k⩽N-1 \end{gathered}$$

5.2 根据几何对称分类:

• 对称序列(symmetric sequence)
• 反对称序列(Anti-symmetric sequence)
• 一个长度为N 的对称序列x[n] 满足以下条件：
  $$x[n]=x[N-1-n]$$
  • 当N 为奇数时，x[n] 关于n = (N − 1)/2 对称
  • 当N 为偶数时，x[n] 关于半样本点n = (N − 1)/2 对称
• 一个长度为N 的反对称序列x[n] 满足以下条件：
  $$x[n]=-x[N-1-n]$$
  • 当N 为奇数时，x[n] 关于n = (N − 1)/2 反对称
  • 当N 为偶数时，x[n] 关于半样本点n = (N − 1)/2 反对称

6 DFT对称关系

• 复数序列的DFT对称性质

• 根据共轭定理：
  $$x^{\ast }[n]\rightleftarrows X^{\ast }[<-k{>}_N]$$
  可得到以下的复数序列的DFT对称性质：

1. 序列x[n]的实部$x_{re}[n]$的DFT为$X[k]$的圆周共轭对称部分$X_{cs}[k]$：
   $$x_{re}[n]=\frac{1}{2}(x[n]+x^{\ast }[n])\rightleftarrows \frac{1}{2}(X[k]+X^{\ast }[<-k{>}_N])=X_{cs}[k]$$
2. 序列x[n]的虚部$j{x}_{im}[n]$的DFT为X[k]的圆周共轭反对称部分$X_{ca}[k]$：
   $$j{x}_{im}[n]=\frac{1}{2}(x[n]-x^{\ast }[n])\rightleftarrows \frac{1}{2}(X[k]-X^{\ast }[<-k{>}_N])=X_{ca}[k]$$

• 根据圆周共轭时间反转定理：
  $$x^{\ast }[<-k{>}_N]\rightleftarrows X^{\ast }[k]$$
  可得到以下的复数序列的DFT对称性质：

1. 序列x[n]的圆周共轭对称部分$x_{cs}[n]$的DFT 为X[k] 的实部$X_{re}[k]$：
   $$x_{cs}[n]=\frac{1}{2}(x[n]+x^{\ast }[<-n{>}_N])\rightleftarrows \frac{1}{2}(X[k]+X^{\ast }[k])=X_{re}[k]$$
2. 序列x[n] 的圆周共轭反对称部分$x_{ca}[n]$的DFT 为X[k]的虚部$j{X}_{im}[k]$：
   $$j{x}_{ca}[n]=\frac{1}{2}(x[n]-x^{\ast }[<-n{>}_N])\rightleftarrows \frac{1}{2}(X[k]-X^{\ast }[k])=j{X}_{im}[k]$$

• 实数序列的DFT对称性质
• 实数序列是复数序列当虚部为零时的特殊情况：
  $$x[n]\in R$$

1. 共轭等于信号本身$x[n]=x^{\ast }[n]$，满足圆周共轭对称：
   $$X[k]=X^{\ast }[⟨-k⟩N]$$
   2 实数序列DFT的实部满足圆周对称：
   $$X_{re}[k]=X_{re}[⟨-k⟩N]$$
   3 实数序列DFT 的虚部满足圆周反对称：
   $$X_{im}[k]=-X_{im}[⟨-k⟩N]$$

7 离散傅里叶变换定理

1、线性定理
$$a{x}_1[n]+b{x}_2[n]⟷a{X}_1[k]+b{X}_2[k]$$

2、圆周时移定理
$$x[<n-n_0{>}_N]=W_N^{k{n}_0}X[k]$$

3、圆周频移定理
$$W_N^{-k{n}_0}x[n]=X[<k-k_0{>}_N]$$

4、对偶定理
$$X^{\ast }[n]=Nx[<-k{>}_N]$$

5、圆周卷积定理
$$g[n]Ⓝh[n]⟷G[k]H[k]$$

6、调制定理
$$g[n]h[n]⟷\frac{1}{N}G[k]ⓃH[k]$$

7、帕塞瓦尔定理
$$\sum _{n=0}^{N-1}|x[n]{|}^2=\frac{1}{N}\sum _{k=0}^{N-1}|X[k]{|}^2$$

8、共轭定理
$$x^{\ast }[n]⟷X^{\ast }[<-k{>}_N]$$

9、圆周时间反转定理
$$x[<-k{>}_N]⟷X[<-k{>}_N]$$

8 计算实序列的DFT

8.1 用单个N点DFT计算两个实序列的N点DFT

设$g[n]和h[n]$是长度为N的两个实序列，$G[k]和H[k]$分别代表其N点DFT。这两个N点DFT可以通过长度为N的复序列$x[n]$的单个N点DFT序列$X[k]$来有效计算，$x[n]$定义为：
$$x[n]=g[n]+jh[n]$$
可以求得：
G [ k ] = 1 2 { X [ k ] + X ∗ [ < − k > N ] } H [ k ] = 1 2 { X [ k ] − X ∗ [ < − k > N ] } G[k] = \frac 12\{X[k] + X^*[<-k>_N]\}\\ H[k] = \frac 12\{X[k] - X^*[<-k>_N]\} G[k]=21​{ X[k]+X∗[<−k>N​]}H[k]=21​{ X[k]−X∗[<−k>N​]}

8.2 用单个N点DFT计算一个个实序列的2N点DFT

令$v[n]$是长度为2N的实序列，$V[k]$表示该实序列的2N点DFT。定义两个长度为N的实序列$g[n]和h[n]$为：
$$\begin{gathered} g[n]=v[2n] \\ h[n]=v[2n+1] \end{gathered}$$
$G[k]和H[k]$表示他们的N点DFT。定义一个长度为N的复序列$x[n]=g[n]+jh[n]$可以从序列$x[n]$的N点DFT$X[k]$来计算DFT$G[k]和H[k]$
$$\begin{gathered} V[k]=\sum _{n=0}^{2N-1}v[n]W_{2N}^{nk}=\sum _{n=0}^{N-1}v[2n]W_{2n}^{2nk}+\sum _{n=0}^{N-1}v[2n+1]W_{2N}^{2n+1} \\ =\sum _{n=0}^{N-1}g[n]W_N^{nk}+\sum _{n=0}^{N-1}h[n]W_N^{nk}{W}_{2N}^k \\ =\sum _{n=0}^{N-1}g[n]W_N^{nk}+W_{2N}^k\sum _{n=0}^{N-1}h[n]W_N^{nk} \\ =G[<k{>}_N]+W_{2N}^{k}H[<k{>}_N] \end{gathered}$$

9 用DFT实现线性卷积

9.1 两个有限长序列的线性卷积

为了用基于DFT的方法实现线性卷积，先用（M-1）个零对$g[n]$进行补零得到长度为L的序列$g_c[n]$，接着用（N-1）个零对$h[n]$进行补零得到长度为L的序列$h_c[n]$。然后分别计算$g_c[n]$和$h_c[n]$的L点DFT，得到$G_c[k]和H_c[k]$，最后对乘积$G_c[k]\ast H_c[k]$做L点IDFT，得到$y_L[n]$。这个流程如下图所示：

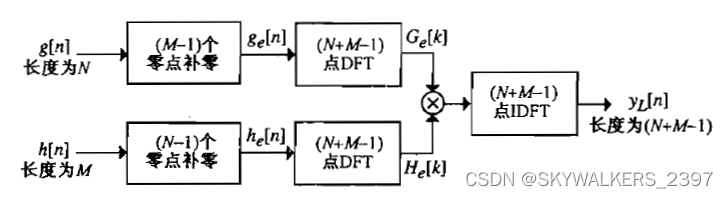
9.2 有限长序列和无限长序列的线性卷积

另$h[n]$是一个长度为M的有限长序列，而$x[n]$是一个无限长序列（或者是一个长度远大于M的有限长序列）。计算两者的线性卷积
重叠相加法

1. 首先分割$x[n]$（不失一般性，假定它为因果序列）,得到一组长度为N的连续有限长子序列$x_m[n]$:
   $$x[n]=\sum _{m=0}^{\infty }{x}_m[n-mN]$$
   其中
   $$x_m[n]=\{\begin{array}{r}x[n+mN],0⩽n⩽N-1\\ 0,其他\end{array}$$
2. 将$x_m[n]$代入卷积计算公式中得：
   $$\begin{gathered} y[n]=\sum _{l=0}^{M-1}h[l](\sum _{m=0}^{\infty }{x}_m[n-l-mN]) \\ =\sum _{m=0}^{\infty }{y}_m[n-mN] \end{gathered}$$
   其中：
   $$y_m[n]=h[n]\otimes x_m[n]$$
3. 计算完每个短卷积后，每两个相邻的短卷积之间会发生重叠，因此，在进行最后的加法时，需要将重叠部分进行相加（重叠部分为$rN⩽n⩽rN+M-2$)。

重叠保留法
将$x[n]$分割为重叠的块$x_m[n]$，在计算过程中，保留$h[n]和x_m[n]$的圆周卷积中与$h[n]$和$x_m[n]$的线性卷积对应的项，丢弃圆周卷积的其他部分。
在长度为M的序列$h[n]$和长度为N的序列$x[n]$的N点圆周卷积中，其中$N>M$，通常最前面的$M-1$个样本是不正确的并被丢弃，而余下的$N-M+1$个样本对应于$h[n]和x[n]$的线性卷积的正确样本。